laborat / 4.1.Определение коэффициента самоиндукции методом Жубера

Учреждение образования

«ВЫСШИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ»

кафедра математики и физики

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА САМОИНДУКЦИИ МЕТОДОМ ЖУБЕРА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ №4.1

по дисциплине

«ФИЗИКА»

для студентов всех специальностей

Учреждение образования

«ВЫСШИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ»

кафедра математики и физики

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА САМОИНДУКЦИИ МЕТОДОМ ЖУБЕРА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ №4.1

по дисциплине

«ФИЗИКА»

для студентов всех специальностей

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА САМОИНДУКЦИИ МЕТОДОМ ЖУБЕРА

ЦЕЛЬ РАБОТЫ

Исследовать зависимость коэффициента самоиндукции от положения подвижного сердечника.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ

Исследуемая катушка самоиндукции с вставным сердечником; реостат; амперметр постоянного тока; вольтметры постоянного и переменного тока; понижающий трансформатор; ключ; соединительные провода.

ЭЛЕМЕНТЫ ТЕОРИИ

При всяком изменении тока в электрической цепи меняется и величина связанного с ним магнитного потока. Так как связанный с током магнитный поток пронизывает площадь, ограниченную контуром цепи, то при изменении тока в какой-нибудь электрической цепи в ней самой возникает электродвижущая сила индукции, называемая электродвижущей силой самоиндукции. Величина электродвижущей силы самоиндукции определяется по формуле:

, (1)

где ‑ поток магнитной индукции, связанный с током, текущим по цепи.

Величина магнитного потока, т.е. число линий индукции, охватывающих контур цепи, пропорциональна току, протекающему в цепи:

(2)

Коэффициент пропорциональности L в этой зависимости носит название индуктивности или коэффициента самоиндукции контура. Если ток , тогда , т.е. индуктивность контура равна потоку магнитной индукции, пронизывающему площадь, ограниченную контуром, когда по этому контуру течет ток, равный единице. Величина этого коэффициента зависит от размеров и формы контура и от магнитной проницаемости среды.

Электрический ток не может существовать без связанного с ним окружающего его магнитного поля, поэтому всякий контур обладает индуктивностью. Однако можно изготовить контур, индуктивность которого будет достаточно мала. Для этого необходимо максимально сблизить участки контура, по которым ток проходит в противоположных направлениях (шнур осветительной сети, бифилярная обмотка в эталонных резисторах).

Высокой индуктивностью обладает соленоид с большим числом близко расположенных витков и большой площадью сечения. Индуктивность еще больше увеличивается при наличии в соленоиде железного сердечника.

Величину электродвижущей силы самоиндукции, возникающей при изменении тока в контуре, можно получить, подставив в формулу (1) значения из формулы (2). Тогда:

(3)

Если параметры контура не меняются при изменении тока, то выносится за знак производной как постоянная величина:

(4)

Здесь ‑ величина положительная. Следовательно, знак электродвижущей силы самоиндукции определяется знаком . Если , то ‑ электродвижущая сила самоиндукции направлена навстречу возрастающему току. Если , т.е. если ток в контуре уменьшается, то , и направление электродвижущей силы самоиндукции совпадает с направлением тока.

Формула (4) дает возможность дать другое определение индуктивности. Производная от тока по времени есть скорость изменения тока. Если она будет равна единице, то . Это значит, что индуктивность контура равна электродвижущей силе самоиндукции, возникающей в контуре при равномерном изменении в ней тока на одну единицу за единицу времени (при скорости изменения тока, равной единице)

Из формулы (2) вытекает единица размерности коэффициента самоиндукции. В системе единиц СИ она называется генри (Гн).

1 Гн ‑ есть индуктивность такого уединенного контура, площадь которого пронизывается магнитным потоком в 1 Вб, если в нем идет ток силой 1 А.

1 Гн = 1 Вб/А.

МЕТОДИКА ЭКСПЕРИМЕНТА И ОПИСАНИЕ УСТАНОВКИ

При прохождении по проводнику переменного тока в нем появляется ЭДС самоиндукции. Текущий по проводнику с индуктивностью ток меняется не только из-за изменения приложенного напряжения, но и вследствие действия возникающей в нем ЭДС самоиндукции. Это же действие оказывается в том, что максимального значения ток достигает позже, чем приложенное напряжение. В случае, если проводник обладает ничтожным омическим сопротивлением, ток отстает от напряжения на 1/4 периода, сдвиг фаз между приложенным напряжением и силой тока равен . При этом максимальное (амплитудное) значение тока будет равно

, (5)

где ‑ циклическая частота; ‑ напряжение.

Рис.1

Сравнение формулы (5) с законом Ома показывает, что величина играет роль сопротивления. Она называется индуктивным сопротивлением.

Чтобы индуктивное сопротивление было выражено в омах, нужно выразить в генри. Индуктивное сопротивление зависит не только от индуктивности контура, но и пропорционально циклической частоте тока .

Теория переменных токов показывает, что при наличии в цепи омического сопротивления и индуктивного сопротивления полное сопротивление переменному току равно

. (6)

Пользуясь формулой (6), можно определить индуктивность соленоида методом Жубера, измеряя его омическое и индуктивное сопротивления. Для этой цели, подключив исследуемую катушку в цепь постоянного тока и измеряя силу тока и напряжение , определяют омическое сопротивление:

. (7)

Подключив эту же катушку в цепь переменного тока, и измеряя силу тока i и напряжение u, определяют полное сопротивление:

(8)

Рабочую формулу для вычисления коэффициента самоиндукции можно получить, если выражение (6) возвести в квадрат и из него выразить :

Пользуясь током от сети с частотой =50 Гц и учитывая, что , окончательно получим

(9)

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Схема цепи для измерений на постоянном токе приведена на рис.1,

Рис.1

где ‑ источник постоянного тока; ‑ исследуемая катушка; ‑ реостат;  ‑ амперметр; ‑ вольтметр постоянного тока.

2. Замкнув ключ К, пропускают через катушку постоянный ток. Для 4-х произвольно выбранных значений силы тока определяют на концах катушки напряжения, соответствующие этим токам, при следующих условиях опытов: а) отсутствует железный сердечник в исследуемой катушке (l=0); б) железный сердечник вставлен в катушку на 1/4 его длины l; в) железный сердечник вставлен в катушку на 1/2 его длины l; г) железный сердечник вставлен в катушку на 3/4 его длины l. Изменения тока осуществляются вращением ползунка реостата R.

3. . Данные измерений занести в таблицу.

4. Схема цепи для измерений на переменном токе приведена на рис.2.

Рис.2

На этой схеме ‑ понижающий трансформатор; ‑ исследуемая катушка; ‑ реостат; и ‑ амперметр и вольтметр переменного тока.

5. .Замкнув ключ В, пропускают через катушку переменный ток. Для 4-х произвольно выбранных значений силы тока определяют на концах катушки напряжения, соответствующие этим токам, при следующих условиях опытов: а) отсутствует железный сердечник в исследуемой катушке (l=0); б) железный сердечник вставлен в катушку на 1/4 его длины l; в) железный сердечник вставлен в катушку на 1/2 его длины l; г) железный сердечник вставлен в катушку на 3/4 его длины l. Изменения силы переменного тока осуществляются вращением ползунка реостата R.

6. Данные измерений занести в таблицу.

6. Пользуясь расчетной формулой (9) и таблицей результатов измерений, рассчитать искомое значение индуктивности и записать в окончательном виде для каждого положения сердечника. Здесь ‑ среднеквадратичное отклонение, вычисляемое по формуле:

,

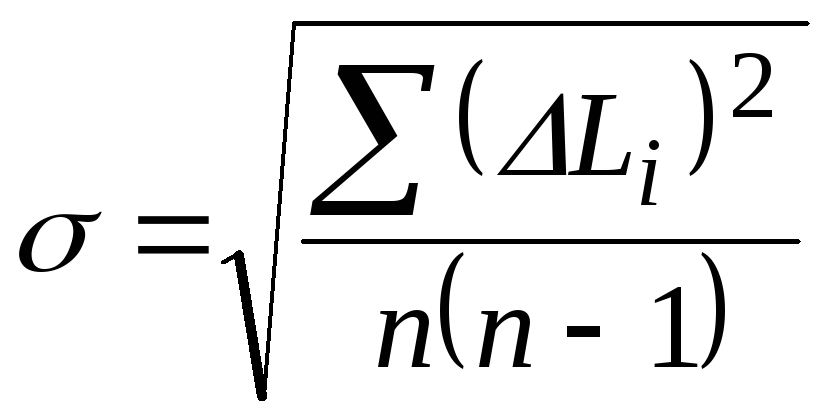где ‑ абсолютная погрешность искомой величины.

Таблица измерений при длине l вводимого в катушку сердечника:

№ п/п	I, A (пост. ток)	U, B (пост. ток)	R, Oм	I, A (перем. ток)	U, B (перем. ток)	Z, Oм	L, Гн	Lср, Гн	, Гн
1.
2.
3.
4.

№ п/п	I, A (пост. ток)	U, B (пост. ток)	R, Oм	I, A (перем. ток)	U, B (перем. ток)	Z, Oм	L, Гн	Lср, Гн	, Гн
1.
2.
3.
4.

№ п/п	I, A (пост. ток)	U, B (пост. ток)	R, Oм	I, A (перем. ток)	U, B (перем. ток)	Z, Oм	L, Гн	Lср, Гн	, Гн
1.
2.
3.
4.

№ п/п	I, A (пост. ток)	U, B (пост. ток)	R, Oм	I, A (перем. ток)	U, B (перем. ток)	Z, Oм	L, Гн	Lср, Гн	, Гн
1.
2.
3.
4.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем заключается явление самоиндукции?

1. Что называется коэффициентом самоиндукции? В каких единицах он измеряется?

1. Дать описание метода Жубера для определения коэффициента самоиндукции.

1. Вывести рабочую формулу для определения коэффициента самоиндукции.

7