laborat / 3.3Электродвижущая сила источника

Учреждение образования

«ВЫСШИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ»

ОПРЕДЕЛЕНИЕ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ ИСТОЧНИКА ТОКА МЕТОДОМ КОМПЕНСАЦИИ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ №3.3

по дисциплине

«ФИЗИКА»

для студентов всех специальностей

Минск 2006

ОПРЕДЕЛЕНИЕ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ ИСТОЧНИКА ТОКА МЕТОДОМ КОМПЕНСАЦИИ

ЦЕЛЬ РАБОТЫ

Определить ЭДС не менее трех неизвестных источников.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ

1. Набор источников тока.

2. Нормальный элемент.

3. Реохорд.

4. Гальванометр.

5. Переключатели.

ЭЛЕМЕНТЫ ТЕОРИИ

Условием движения электрических зарядов в проводнике является наличие в нем электрического поля, которое создается и поддерживается особыми устройствами, получившими название источников тока.

Основной величиной, характеризующей источник тока, является его электродвижущая сила. Электродвижущей силой источника (сокращенно ЭДС) называется скалярная физическая величина – количественная мера способности источника создавать на его зажимах (полюсах) разность потенциалов. Она равна работе сторонних сил по перемещению заряженной частицы с положительным единичным зарядом от одного полюса источника к другому, т.е.

. (1)

В СИ ЭДС измеряется в вольтах (В), т.е. в тех же единицах, что и напряжение.

Сторонние силы источника – это силы, которые осуществляют разделение зарядов в источнике и тем самым создают на его полюсах разность потенциалов. Эти силы могут иметь различную природу, но только не электрическую (отсюда и название).

Если электрическую цепь разделить на два участка – внешний, с сопротивлением R, и внутренний, с сопротивлением r, то ЭДС источника тока окажется равной сумме напряжений на внешнем и внутреннем участках цепи:

. (2)

По закону Ома напряжение на любом участке цепи определяется величиной протекающего тока и его сопротивлением:

.

Так как , следовательно

, (3)

т.е. напряжение на полюсах источника при замкнутой цепи зависит от соотношения сопротивлений внутреннего и внешнего участков цепи. Если , то приблизительно равно U. На этом основано приблизительное определение ЭДС при помощи вольтметра с большим сопротивлением, подключаемого к полюсам источника. Только в отсутствие тока в источнике его ЭДС будет равна напряжению на полюсах.

Величину ЭДС можно определить точно электростатическим или компенсационным методом. При измерении ЭДС электростатическим методом цепь остается разомкнутой, т.к. измерение разности потенциалов на полюсах источника проводится прибором, не потребляющим тока (электрометр, электростатический вольтметр). При измерении ЭДС компенсационным методом цепь источника замкнута, но необходимые отсчеты делаются в моменты отсутствия тока в источнике.

Компенсационный метод определения ЭДС

Сущность метода компенсации в измерении ЭДС заключается в подборе и определении напряжения на участке электростатической цепи, равного ЭДС исследуемого источника.

Схема электрической цепи для определения ЭДС методом компенсации изображена на рис.1.

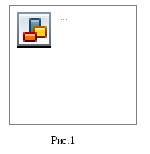
Два источника ЭДС  и _x включены навстречу друг другу. Сопротивления R₁ и R₂ выполнены в виде однородной проволоки, натягиваемой между точками А и В, а точка С определяется скользящим контактом (при необходимости очень высокой точности измерений R₁ и R₂ представляют собой магазины сопротивлений).

Выберем положительные направления токов, как показано на рис.1, и применим к рассматриваемой схеме правила Кирхгофа. Первое правило для точек А и С дает

(4)

Второе правило для контуров АBCA и А_xСА приводит к уравнениям:

(5)

(6)

Эти уравнения вполне определяют все неизвестные токи. Однако мы ограничимся частным случаем и предположим, что сопротивления R₁ и R₂ подобраны таким образом, что ток I_x в цепи гальванометра G равен 0. В этом случае уравнения (4)-(6) принимают вид

,

Из двух последних уравнений находим

, (7)

где R – полное сопротивление струны, которое не зависит от положения скользящего контакта С.

Предположим теперь, что вместо источника с неизвестной ЭДС _x мы включили в схему другой источник _н с известной ЭДС и перемещением контакта С, а следовательно, изменением переменных сопротивлений, вновь добились компенсации (I₁=0). Для этого вместо сопротивления r_x потребовалось ввести сопротивление r_н. Тогда

. (8)

Разделив почленно (7) на (8), получим

. (9)

Это равенство и лежит в основе сравнения ЭДС методом компенсации.

Отметим, что отношение сравниваемых ЭДС не зависит от внутренних сопротивлений источников и от других сопротивлений схемы, а определяется только отношением сопротивлений участка цепи, к которому поочередно подключают сравниваемые источники ЭДС. Не требуется знать и ЭДС вспомогательного источника , которая только должна быть достаточно постоянна во время измерения и больше обеих сравниваемых ЭДС и .

МЕТОДИКА ЭКСПЕРИМЕНТА И ОПИСАНИЕ УСТАНОВКИ

ЭДС гальванического элемента в данной работе определяется путем ее сравнения с ЭДС нормального элемента =1,00 В. Напряжение между электродами этого и подобных ему других нормальных элементов весьма постоянно. Поэтому они играют в электрической измерительной технике ту же роль, что и эталоны длины (метр) и массы (килограмм) при измерении механических величин.

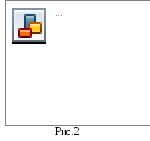
Схема соединения приборов изображена на рис.2, где  - вспомогательный источник питания; АВ – струна реохорда со скользящим контактом С; и – нормальный и исследуемый элементы; G – гальванометр; П – двухполюсный переключатель; К – ключ, замыкающий цепь вспомогательного источника питания.

Решение равенства (9) относительно позволяет получить формулу для вычисления ЭДС исследуемого элемента

(10)

Струна АВ является однородным проводником постоянного сечения.

Сопротивления ее участков цепи R₁ и R_1н (длиной l_x и l_н соответственно), входящих в (10), можно выразить как

R₁ и R_1н =.

Подставляя эти значения в (10) , окончательно получаем расчетную формулу для определения ЭДС исследуемого источника тока

. (11)

Как видим, в этой формуле отношение сопротивлений участков струны равно отношению их соответствующих длин.

Метод компенсации практически можно осуществить при следующих условиях:

1. ЭДС основного источника должна быть больше ЭДС как эталонного, так и исследуемого элементов;

2) цепь следует замыкать на малые промежутки времени, достаточные для фиксирования наличия или отсутствия тока в гальванометре.

Порядок выполнения работы

1. Собрать схему, изображенную на рис.2 (если она собрана, убедиться в ее соответствии рисунку).

2. Включить элемент в цепь гальванометра (тумблер П в верхнем положении). Перемещая контакт С, добиться компенсации этого элемента напряжением на участке струны АС, т.е. установления «0» на гальванометре. Измерить длину участка струны l_н, при которой осуществляется компенсация.

3. Включить один из пяти неизвестных элементов в цепь гальванометра (тумблер П в нижнем положении). Перемещая контакт С, добиться компенсации этого элемента напряжением на участке струны АС, о чем свидетельствует установление «0» на гальванометре. Измерить длину участка струны l_х, при которой осуществляется компенсация.

4. Рассчитать ЭДС неизвестного элемента по формуле (11).

5. Повторить измерения, указанные в пунктах 2-4 еще несколько раз для получения более точных результатов. Рассчитать среднее значение ЭДС и погрешность результата. Результаты измерений и расчетов записать в таблицу 1 с обязательным указанием размерности всех используемых величин.

Таблица 1

№ элемента	№ опыта (i)	lн	lх	xi	xср	|xi|	
	1
1	2
	3

6. Окончательный результат записать в виде , где s ‑ среднеквадратичное отклонение, вычисляемое по формуле:

,

где n – число измерений для одного элемента.

7. Повторить задания 2-7 для других элементов _х. Составить для них аналогичные таблицы.

Контрольные вопросы

1. Дать определение электродвижущей силе источника. Какова ее размерность?

2. Какие силы вызывают разделение зарядов в источниках питания? Привести примеры.

3. Как можно определить значение ЭДС источника?

4. Какие методы позволяют рассчитать ЭДС источника с большой степенью точности? В чем их сходство?

5. В чем сущность метода компенсации?

6. Вывести расчетную формулу для определения ЭДС источника методом компенсации.

Литература

1. С.Г. Калашников. Электричество. М.: «Наука», 1977 г.

2. И.Е. Иродов. Основные законы электромагнетизма. М.: «Высшая школа», 1983 г.

7