
- •Тема 16. Квантовая оптика.
- •Вопрос 2. Энергетическая светимость. Излучательная, отражательная и поглощательная способность тела.
- •Вопрос 3. Абсолютно черное тело. Серое тело. Закон Кирхгофа.
- •Вопрос 4. Закон Стефана-Больцмана. Законы Вина.
- •Вопрос 5. Формула Планка.
- •Вопрос 6. Оптическая пирометрия.
Вопрос 5. Формула Планка.
Выход из создавшейся ситуации нашел немецкий физик М. Планк.
В 1900 г. он впервые выдвинул гипотезу о дискретных значениях энергии осциллятора.
Согласно этой гипотезе энергия осциллятора с собственной частотой ν может принимать лишь определенные дискретные (квантованные) значения, отличающиеся на целое число элементарных порций − квантов энергии: εν = hν, где h= 6,625·10-34 Дж·с − постоянная Планка (квант действия). Тогда полная энергия осциллятора будет равна целому числу квантов
![]() ,
(
,
(![]() ). (16.17)
). (16.17)
Согласно этой гипотезе Планк моделировал реальное твердое тело с помощью системы квантовых осцилляторов. Выполнив усреднение энергии осциллятора с помощью распределения Больцмана, Планк получил выражение для среднего значения энергии, приходящейся на одну колебательную степень свободы осциллятора:
 .
(16.18)
.
(16.18)
Подставив соотношение (16.18) в формулу Рэлея – Джинса (16.14), Планк получил формулу для излучательной способности АЧТ как функцию от частоты излучения:
 .
(16.19)
.
(16.19)
Эта формула как функция от длины волны излучения имеет вид:
 ,
(16.20)
,
(16.20)
именно ее чаще всего используют в экспериментальных работах.
Из формулы Планка вытекают все законы теплового излучения тел.
В
области малых частот, т.е. при условии,
что квант энергии во много раз меньше
средней энергии осциллятора (h![]() ,
формула Планка совпадает с формулой
Релея—Джинса. Для доказательства этого
разложим функцию eh
,
формула Планка совпадает с формулой
Релея—Джинса. Для доказательства этого
разложим функцию eh![]() в ряд:
в ряд:
eh![]() =1+
=1+![]() )
)![]() +
+![]() (
(![]() )
)![]() +…
(16.21)
+…
(16.21)
и, ограничившись первыми двумя членами разложения, из (16.19) получаем формулу Релея—Джинса (16.14):
R(![]() =
=![]() .
.
В
предельном случае больших частот (![]() >>1)
единицей в знаменателе формулы (16.19)
можно пренебречь, тогда получим формулу
>>1)
единицей в знаменателе формулы (16.19)
можно пренебречь, тогда получим формулу
![]() ,
(16.22)
,
(16.22)
которая совпадает с выражением (16.12), т.е. с формулой Вина, причем, функция F(ν/Т) представляет собой выражение
![]() ,
,
которое действительно зависит от отношения частоты к температуре. График функции Вина показан на рис. 16.5. Функции Вина совпадает с формулой Планка только в области больших частот.
Интегральную
излучательную способность АЧТ (закон
Стефана—Больцмана) можно получить,
проинтегрировав выражение (16.20) по длинам
волн в интервале от 0 до
![]() :
:
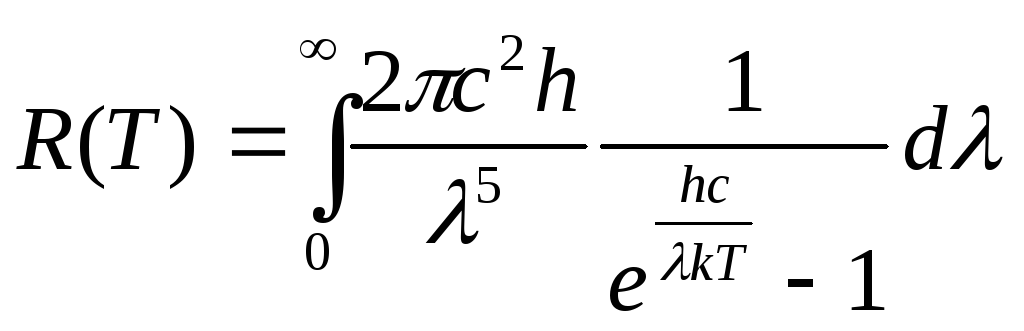 .
(16.23)
.
(16.23)
Произведем
замену переменной. Обозначим
![]() ,
тогда подстановка
,
тогда подстановка![]() и
и![]() приводит выражение (16.21) к виду
приводит выражение (16.21) к виду
![]() ,
(16.24)
,
(16.24)
где
![]() .
Так как
.
Так как![]() ,
то
,
то
![]() .
(16.25)
.
(16.25)
Как видим, величина (постоянная Стефана-Больцмана) выражается через постоянные величины c, h, k.
Анологично, исследуя функцию (16.22) по переменной ν на экстремум, можно получить значение постоянной Вина, которая выражается также через постоянные с, h и k, и выполнить проверку закона смещения Вина.
Таким образом, формула Планка не только хорошо согласуется с
экспериментальными данными, но и содержит в себе частные законы теплового излучения. Следовательно, формула Планка является полным решением основной задачи теплового излучения, поставленной Кирхгофом. Ее решение стало возможным лишь благодаря революционной квантовой гипотезе Планка.
