Вопрос 6. Уравнение Шредингера для атома водорода. Векторная модель атома.

Рассмотрим теперь квантово-механическую теорию атомов. Она сохраняет некоторые аспекты старой теории Бора. Например, электроны могут находиться в атоме только в дискретных состояниях с определенной энергией; при переходе электрона из одного состояния в другое испускается или поглощается фотон. Но квантовая механика – не просто обобщение теории Бора. Она представляет собой гораздо более глубокую теорию и рисует совершенно иную картину строения атома. Согласно квантовой механике, не существует определенных круговых орбит электронов, как в теории Бора. В силу волновой природы электрон «размазан» в пространстве, подобно «облаку» отрицательного заряда.

Размытое в пространстве облако является результатом волновой природы электронов. Электронное облако можно также интерпретировать как распределение вероятностей для данной частицы. Мы не можем предсказать траектории, по которой будет двигаться электрон. После измерения его первоначального положения невозможно точно предсказать, где будет находиться электрон в последующие моменты времени. Мы можем лишь вычислить вероятность обнаружения электрона в различных точках. Ясно, что подобная ситуация в корне отличается от классической ньютоновской физики.

Применим уравнение Шредингера к электрону, находящемуся в атоме водорода.

Решение задачи об энергетических уровнях электрона для водорода,

а также водородоподобных систем сводится к задаче о движении электрона в кулоновском поле ядра. Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze (для атома водорода Z = 1), определяется выражением

(21.20)

и зависит только от r – расстояния между электроном и протоном, поэтому задачу с таким видом потенциальной энергии обычно решают в сферической системе координат. В общем случае волновая функция является функцией от всех координат и уравнение Шредингера будет иметь вид:

. (21.21)

Электрон в атоме находится в потенциальной яме, края которой имеют форму гиперболы (рис.21.5).

Очевидно, что решение этой задачи должно быть подобно решению задачи, когда частица находилась в бесконечно глубокой одномерной потенциальной яме с прямоугольными краями.

Рис.21.5.

Так как электрическое поле – центрально-симметрично, то для решения этого уравнения воспользуемся сферической системой координат (r, θ, φ), которые связаны с декартовыми координатами, как это следует из рис. 21.6, соотношениями: x = r sin θ cos φ; y = r sin θ sin φ; z = r cosθ .

Рис. 21.6

Подставив в (21.21) выражение оператора Лапласа в сферических

координатах, получим уравнение Шредингера в следующем виде:

. (21.22)

Строгое решение уравнения (21.22) в соответствии с теорией дифференциаль­ных уравнений дает следующие результаты. Электрон в атоме обладает не произвольным значением энергии, а набором определенных отрицательных дискретных значений E_n:

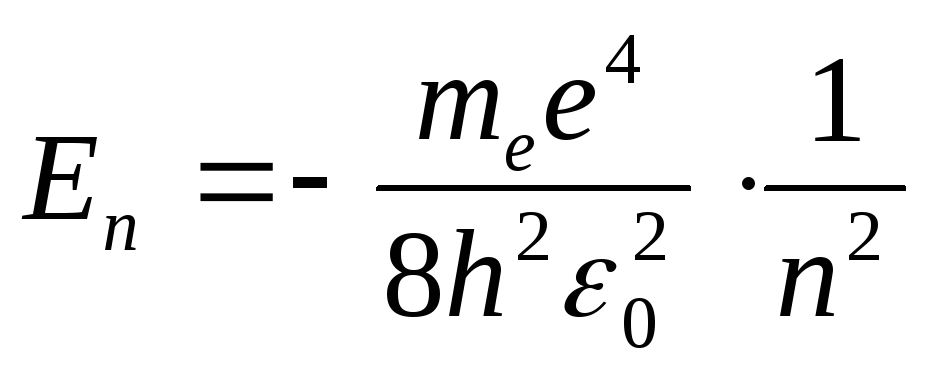, (21.23)

где n – главное квантовое число, принимающее значения 1,2,3.…,∞. Из (21.23) следует, что именно главное квантовое число определяет энергию электрона в атоме: E_n ~ . Выражение для значений энергийEn (21.23) полностью совпадает с результатами теории Бора (19.15). Для атома водорода значение n = 1 соответствует основному состоянию электрона, значение n = ∞ – свободному электрону (E∞ = 0). Отрицательные значения энергии соответствуют связанному состоянию электрона, когда он находится внутри потенциальной ямы и имеет большие отрицательные значения потенциальной энергии (21.20). Положительными значениями энергии электрон обладает в свободном состоянии, когда он покидает пределы атома, и его энергетический спектр становится непрерывным, т.е. область E > 0 соответствует ионизированному атому.

Итак, если Бору пришлось вводить дополнительные гипотезы (постулаты), то в квантовой механике дискретные значения энергии, являясь следствием самой теории, вытекают непосредственно из решения уравнения Шредингера.

Из решения уравнения (21.22) определяются не только значения энергии, но и волновые функции. Причем оказывается, что одному и тому же значению энергии электрона соответствует несколько различных состояний с разными волновыми функциями, соответствующими различным типам движения электрона. Эти типы движения различаются разными значениями орбитального момента импульса и его проекцией на физически выделенное направление Z, совпадающее с направлением вектора напряженности внешнего магнитного поля.

В квантовой механике доказывается, что уравнению Шредингера

удовлетворяют собственные функции Ψ_nlms, определяемые набором четырех квантовых чисел: главного n, орбитального l, магнитного m и спинового m_s.

Момент импульса частицы относительно начала координатО (центр орбиты электрона на рис. 21.7) в классической механике определяется векторным произведением , где вектораиявляются соответственно радиус-вектором частицы и ее импульсом.

Из представлений классической физики следует, что орбитальный момент импульса электрона и пропорциональный ему магнитный моменториентированы перпендикулярно плоскости орбиты электрона и направлены противоположно. Модуль магнитного момента тока, создаваемого движущимся по орбите электроном, равен

. (21.26)

Здесь T – период обращения электрона по орбите, V– его скорость, I − орбитальный ток, S − площадь орбиты.

Магнитный момент обусловлен движением электрона по орбите,

Рис. 21.7

. (21.24)

вследствие чего называется орбитальным магнитным моментом электрона.

Электрон обладает массой m_e, поэтому при движении по орбите он обладает моментом импульса , модуль которого

. (21.25)

Вектор называют орбитальным механическим моментом электрона. Он образует с направлением движения электрона правовинтовую систему. Следовательно, направление векторов ипротивоположны (рис.21.7).

Отношение магнитного момента элементарной частицы к ее механическому моменту называется орбитальным гиромагнитным отношением. Для электрона оно равно

. (21.26)

Такая связь между векторами сохраняется и в теории Бора. Поскольку направления векторов ипротивоположны, выражение, связываюшее магнитный момент и момент импульса движущегося электрона, имеет вид:

. (21.27)

Классическое определение момента импульса в квантовой механике не имеет смысла, поскольку не существует состояния, в котором бы оба вектора иимели определенные значения. В квантовой механике доказывается, что вектор момента импульсане может быть полностью определен как по величине, так и по направлению. Исключением является только случай, когдаи все три проекции одновременно равны нулю:

В квантовой механике модуль момента импульса движущейся микрочастицы определяется выражением:

(21.28)

. Здесь –орбитальное квантовое число. Величина является дискретной (квантовой).

В квантовой механике строго доказывается (это следует из решения уравнения Шредингера), что проекция (L_Z) вектора на направление вектора напряженности внешнего магнитного поля, совмещенного с осьюZ, может принимать лишь целочисленные значения, кратные постоянной :

L_z = mħ. (21.29)

Равенство (21.29) означает, что проекция момента импульса на любое направление квантуется. Проекция любого вектора не может быть больше модуля этого вектора, т.е. . Поэтому в соответствии с выражениями (21.28) и (21.29) имеем:

. (21.30)

Следовательно, максимальное значение равно, тогда. При заданномчислот принимает значений:, которые образуют спектр проекцийна любую выделенную ось, т.е. векторможет принимать (2l + 1) ориентаций в пространстве (рис. 21.8).

Таким образом, квантовое число определяет как модульмомента импульса, так и все возможные значения его проекции на ось. На рис. 6.8 показаны возможные ориентации вектораи его проекции на выделенное направлениемагнитного поля. Например, когда орбитальное квантовое число(средний рисунок 6.8), то; 0;.

Приведенные результаты, определяющие возможные значения и, т.е. дискретность в ориентации вектора, называютпространственным квантованием.

Пространственное квантование на рис. 21.8 представлено лишь схематически (графически): по оси откладывают возможные значенияmћ, рассматривая их как проекции на ось векторадлины. Конечно, это схематическое изображение приведено для наглядности. Ведьорбитальный механический момент электрона принципиально не имеет определенных направлений в пространстве.

На рис. 21.8 показаны возможные ориентации вектора в состоянияхs, p, d.

Рис.21.8

Различные состояния электрона в атоме обозначают малыми буквами латинского алфавита в зависимости от значения орбитального квантового числа l, табл. 1. Электрон в этих состояниях называется соответственно s-, p-, d-электроном и т. д. Значение главного квантового числа n указывают перед символом состояния с данным l: электрон в квантовом состоянии с n=1 и l=0 обозначают символом 1s, при n=2 и l=0 − 2s, при n=2 и l=1 − 2p и т. д.

Таблица 1.

Обозначение состояний электрона в атоме

Квантовое число l	0	1	2	3	4
Символ состояния	s	p	d	f	g

Согласно выражениям (21.27), (21.28), (21.29) дискретный спектр разрешенных значений величины модуля орбитального магнитного момента P_m и его проекции на выделенное направление Z для движущегося электрона определяются как

и (21. 31)

. (21. 32)

Ориентация вектора в пространстве изображается аналогично вектору, приведенному на рис. 21.8.

Спин электрона. В 1922 году немецкие физики О. Штерн и В. Герлах измерили магнитные моменты Pm атомов различных химических элементов. Для химических элементов первой группы таблицы Менделеева магнитный момент атома равен магнитному моменту валентного электрона, т.е. одного электрона.

Идея опыта заключалась в измерении силы, действующей на атом в сильно неоднородном магнитном поле. Неоднородность магнитного поля должна быть такова, чтобы она сказывалась на расстояниях порядка размера атома. Только при этом можно было получить силу, действующую на каждый атом в отдельности.

Схема опыта изображена на рис. 21.9. В колбу с вакуумом 10^-5 мм рт. ст. помещался серебряный шарик К и нагревался до температуры испарения. Затем атомы серебра, вылетающие из колбы со скоростью около 100 м/с, пропускались через щелевые диафрагмы В и после прохождения через резко неоднородное магнитное поле попадали на фотопластинку А.

Если бы момент импульса атома и его магнитный моментмогли принимать произвольные ориентации в пространстве (т.е. в магнитном поле), то было бы непрерывное распределение атомов серебра на фотопластинке с большой плотностью попаданий в середине. Но на опыте были получены совершенно неожиданные результаты: на фотопластинке получилисьдве резкие полосы – все атомы отклонялись в магнитном поле двояким образом, соответствующим лишь двум возможным ориентациям магнитного момента.

Рис. 21.9

Этим доказывался квантовый характер магнитных моментов электронов.

Таким образом, для атомов серебра Штерн и Герлах получили, что проекция магнитного момента атома (электрона) на направление магнитного поля численно равна магнетону Бора, см. (21.31).

Опыты Штерна и Герлаха не только подтвердили квантование моментов импульсов в магнитном поле, но и дали экспериментальное подтверждение тому, что магнитные моменты электронов тоже состоят из некоторого числа «элементарных моментов», т.е. имеют дискретную природу. Единицей измерения магнитных моментов электронов и атомов является магнетон Бора µ_Б (напомним, что ħ – единица измерения механического момента импульса).

Кроме того, в этих опытах было обнаружено новое явление. Валентный электрон в основном состоянии атома серебра имеет орбитальное квантовое число l = 0 (s-состояние). Но при l = 0 и возникает вопрос, квантование какого момента импульса обнаружилось в этих опытах и проекция какого магнитного момента равна магнетону Бора.

В 1925 г. было предположено существование собственного механического момента импульса у электрона (спина) и, соответственно, собственного магнитного момента электрона .

Введение понятия спина сразу объяснило ряд затруднений, имевшихся к тому времени в квантовой механике. И в первую очередь – результатов опытов Штерна и Герлаха.

В современном представлении – спин, как заряд и масса, есть свойство электрона.

П. Дирак впоследствии показал, что существование спина вытекает

из решения релятивистского волнового уравнения Шредингера.

Из общих выводов квантовой механики следует, что спин должен быть квантован: , где – спиновое квантовое число.

Аналогично, проекция спина на ось Z (L_sz) должна быть квантована и вектор может иметь (2s + 1) различных ориентаций в магнитном поле.

Из опытов Штерна и Герлаха следует, что таких ориентаций всего две:

2s +1 =2, а значит s = 1/2, т.е. спиновое квантовое число имеет только одно значение.

Для атомов первой группы, валентный электрон которых находится

в s-состоянии (l = 0), момент импульса атома равен спину валентного электрона. Поэтому обнаруженное для таких атомов квантование момента импульса в магнитном поле является доказательством наличия у спина лишь двух ориентаций во внешнем поле.

Опыты с электронами в p-состоянии подтвердили этот вывод, хотя картина получилась более сложной. Численное значение спина электрона: .

По аналогии с квантованием проекции орбитального момента проекция спинаLsz также квантуется (аналогично, как m = ±l , то и ms = ±s ). Проекция спина на направление внешнего магнитного поля, являясь квантовой величиной, определяется выражением: L_sz = m_s, гдеm_s – магнитное спиновое квантовое число, m_s = ±1/2 , т.е. может принимать только два значения, что и наблюдается в опыте Штерна и Герлаха.

Итак, проекция спинового механического момента импульса на направление внешнего магнитного поля может принимать два значения:

.

Так как мы всегда имеем дело с проекциями, то говоря, что спин имеет две ориентации, имеем в виду две проекции.

Проекция спинового магнитного момента электрона на направление внешнего магнитного поля:

.

Отношение – спиновое гиромагнитное отношение.

С помощью понятия спина электрона удалось также обосновать наблюдаемое на опыте значение гиромагнитного отношения , равное, вместо значения, полученного для орбитальных магнитных моментов.

В 1928 г. английский физик П. Дирак также пришел к выводу о существовании спина электрона на основе анализа полученного им релятивистского уравнения для волновой функции. Оказалось, что модуль проекции собственного магнитного момента на направление вектора напряженности магнитного поля по значению равен магнетону Бора, т.е.

. (21.33)

Ситуация, когда одному и тому же энергетическому уровню соответствует несколько различных квантовых состояний системы (волновые функцииразличаются значениямиl и m), называется вырождением уровней энергии. Уровень энергии называется g-кратно вырожденным, если система в различных состояниях имеет одинаковую энергию. В атоме водорода при заданном числе п орбитальное квантовое число l принимает п значений , а магнитное квантовое числот изменяется в пределах от –l до l, следовательно оно принимает 2l + 1 значение. Кратность вырождения g_n уровня энергии определяется суммой арифметической прогрессии:

. (21.34)

Поскольку в уравнении (21.22) спиновые моменты не учитываются, то энергетические уровни вырождены не только по квантовым числамl и m, но и по спиновому числу . В связи с этим кратность вырожденияg_n квантовых состояний удваивается по сравнению с формулой (21.34), т.е.

. (21.35)

Следует заметить, что классификация состояний электрона с помощью чисел п, l, m и m_s возможна, если не учитывать так называемое спин-орбитальное взаимодействие. Спиновый магнитный момент электрона будет взаимодействовать с магнитным полем, возникающим в результате орбитального движения электрона, и пропорциональным вектору орбитального магнитного момента. Спин-орбитальное взаимодействие является релятивистским эффектом. Это достаточно слабое взаимодействие приводит к тому, что проекции орбитальногои спиновогомоментов не сохраняются, т.е. каждое числоl и S в отдельности не является квантовым числом. Сохраняется лишь полный момент импульса электрона, равный сумме его орбитального и спинового моментов и который символически можно записать так:

. (21.36)

Модуль полного момента импульса электрона определяется формулой

, (21.37)

а четвертое квантовое число определяет проекцию полного момента импульса на некоторую осьZ.

. (21.38)

Так как для электрона s = 1/2 и при числоj = l ± 1/2, а при оно равно 1/2, то квантовые числаидля электрона являются полуцелыми.

Учет спин-орбитального взаимодействия приводит к тому, что уровни энергии , описываемые формулой (21.25), расщепляются на несколько уровней, соответствующих различным значениям квантовых чиселl и j. Это расщепление уровней энергии атома называется тонкой структурой. Тонкую структуру оптического спектра атома водорода (расщепление спектральных линий в дублеты из двух близкорасположенных линий) экспериментально можно наблюдать с помощью спектрометров с большой разрешающей силой. Величина тонкого расщепления энергетических уровней составляет около 10^–5 эВ.

Следует отметить, что атомное ядро, как и электроны атома, обладает магнитным моментом, который взаимодействует с магнитным полем окружающих ядро электронов. Поэтому наряду с тонкой структурой в оптических спектрах атомов наблюдается также и сверхтонкая структура уровней энергии с дополнительным расщеплением спектральных линий на несколько подуровней. Однако величина сверхтонкого расщепления уровней энергии примерно на три порядка меньше величины расщепления энергетических уровней тонкой структуры, т.е. составляет около 10^–8 эВ.

На атом оказывают воздействие внешние электрические и магнитные поля, поскольку он представляет собой систему электрически заряженных частиц.

В 1896 г. голландский физик П. Зееман экспериментально обнаружил расщепление спектральных линий и уровней энергии атомов в магнитном поле. В спектре атома наблюдается расщепление спектральных линий, когда уровень энергии с данным j в магнитном поле расщепляется на подуровней. Расщепление линий спектра атома на три близко расположенные линии называетянормальным (простым) эффектом Зеемана. Нормальный эффект Зеемана наблюдается в случае, когда в отсутствие магнитного поля спектральные линии не имеют тонкой структуры. При аномальном (сложном) эффекте Зеемана каждая спектральная линия расщепляется в магнитном поле на группу равноотстоящих линий, число которых может достигать нескольких десятков.

Эффект Зеемана находит применение в спектроскопии, в устройствах квантовой электроники, например, для измерения напряженностей слабых магнитных полей. На расщеплении энергетических уровней атомов в магнитном поле основано явление электронного парамагнитного резонанса (ЭПР), сущность которого состоит в избирательном поглощении энергии переменного магнитного поля веществом. ЭПР используется при исследовании строения молекул вещества.

Расщепление спектральных линий во внешнем электрическом поле называется эффектом Штарка. Немецкий физик И.Штарк исследовал в

1913 г. расщепление спектральных линий атома водорода во внешнем электрическом поле.

Контрольные вопросы:

1. Какой физический смысл квадрата модуля волновой функции?

2. Какова наименьшая энергия частицы в потенциальной яме с бесконечно высокими стенками?

3. Больше или меньше энергия частицы, находящейся в потенциальной яме с бесконечно высокими «стенками», в состоянии п = 3 по сравнению с состоянием п = 1? Во сколько раз?

4. Какими свойствами микрочастиц обусловлен туннельный эффект?

5. В чем отличие поведения классической и квантовой частиц с энергией Е < U при их движении к прямоугольному потенциальному барьеру конечной ширины?

6. Как изменится коэффициент прозрачности потенциального барьера с ростом его высоты? с увеличением массы частицы? с увеличением полной энергии частицы? с увеличением его ширины в два раза?

7. Может ли частица находиться на дне потенциальной ямы?