Вопрос 2. Полосы равной толщины.

Интерференционная картина от тонкого прозрачного клина переменной толщины была изучена еще Ньютоном. Пусть на такой клин с малым углом φ при вершине, изготовленный из вещества с показателем преломления n, падает почти нормально параллельный пучок лучей от протяженного источника света, (рис.8.3). Для наглядности рисунка угол падения увеличен в десятки раз, по сравнению с его действительным значением.

Теперь лучи, отразившиеся от верхней и нижней поверхностей клина,во всем пространстве над клином не будут строго параллельными. Но и в этом случае отраженные волны от мест клина, для которых толщина удовлетворяет условию (8.1) будут когерентными, и при любом расстоянии экрана Э от клина на нем будет наблюдаться интерференционная картина в виде полос, параллельных вершине клина О.

Рис.8.3

Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, вследствие чего их называют полосами равной толщины. Практически полосы равной толщины наблюдают, поместив вблизи клина линзу и за ней экран. Роль линзы может играть хрусталик, а роль экрана - сетчатка глаза. При наблюдении в белом свете полосы будут окрашенными, так что поверхность пластинки или пленки представляется имеющей радужную окраску. Отчетливость интерференционной картины уменьшается при перемещении от вершины клина к его основанию. При почти нормальном падении света на клин интерференционная картинка локализуется на верхней поверхности клина.

В реальных условиях при наблюдении радужных цветов, например, на масляных пленках в лужах воды или мыльных пленках изменяется как угол падения лучей, так и толщина пленки. Поэтому в этих случаях наблюдаются полосы смешанного типа.

Заметим, что интерференция от тонких пленок может наблюдаться не только в отраженном, но и в проходящем свете.

Вопрос 3. Кольца Ньютона.

Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной толстой стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны (рис. 8.4,а).

а) б)

Рис.8.4

Наблюдаются кольца Ньютона и с системой соприкасающихся плосковогнутой и плосковыпуклой линз с большим радиусом кривизны, причем радиус кривизны плосковогнутой линзы должен быть больше радиуса кривизны плосковыпуклой линзы.

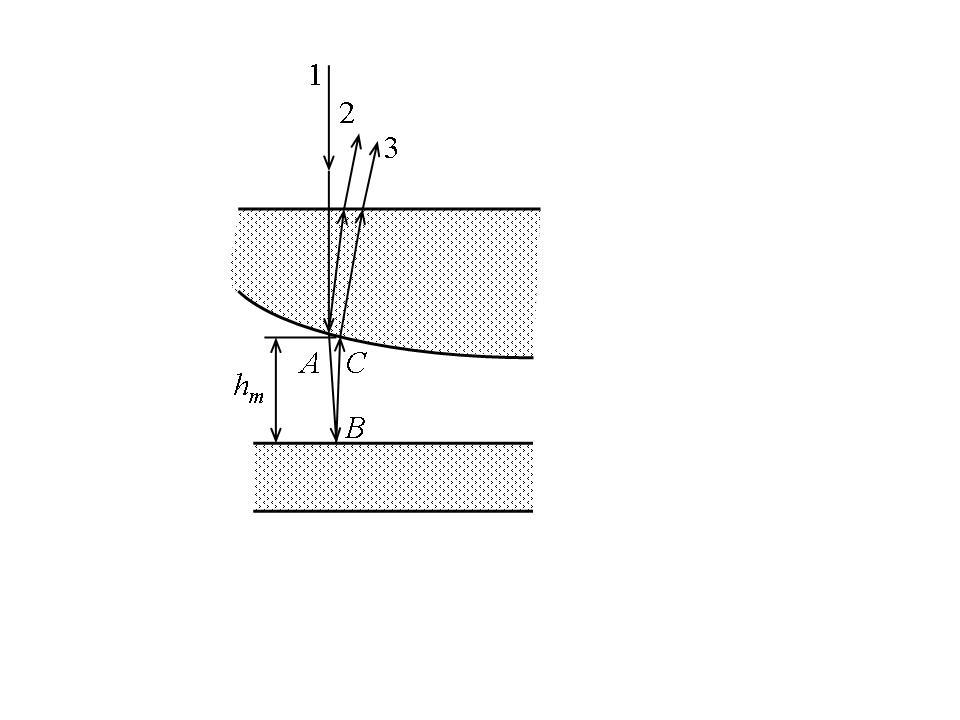
Роль тонкого клина, от поверхности которого отражаются когерентные волны, играет воздушный зазор между стеклянной пластинкой и линзой. Вследствие большой толщины пластинки и линзы за счет отражений от других поверхностей интерференционные полосы не возникают. Луч света 1 (рис. 8.4,б) падает нормально на плоскую поверхность линзы и частично отражается в точке А от верхней (луч 2) и в точке В от нижней (луч 3) поверхностей воздушного зазора. Отраженные лучи 2 и 3 когерентны и при их наложении интерферируют между собой, в результате чего возникают полосы равной толщины. При нормальном падении света на плоскую поверхность линзы полосы равной толщины имеют вид концентрических окружностей, при наклонном падении - эллипсов.

Ввиду малости кривизны поверхности линзы точки А и С находятся на малом расстоянии друг от друга.

Определим оптическую разность хода отраженных лучей и найдем радиусы колец Ньютона при нормальном падении света на пластину. В этом случае sinα = 0 и оптическая разность хода Δ интерферирующих лучей 2 и 3 будет равна удвоенной толщине воздушного зазора, сложенной с дополнительной разностью хода, которая возникает при отражении луча от оптически более плотной среды в точкеВ в результате изменения фазы волны на π (предполагается n_возд = 1):

. (8.2)

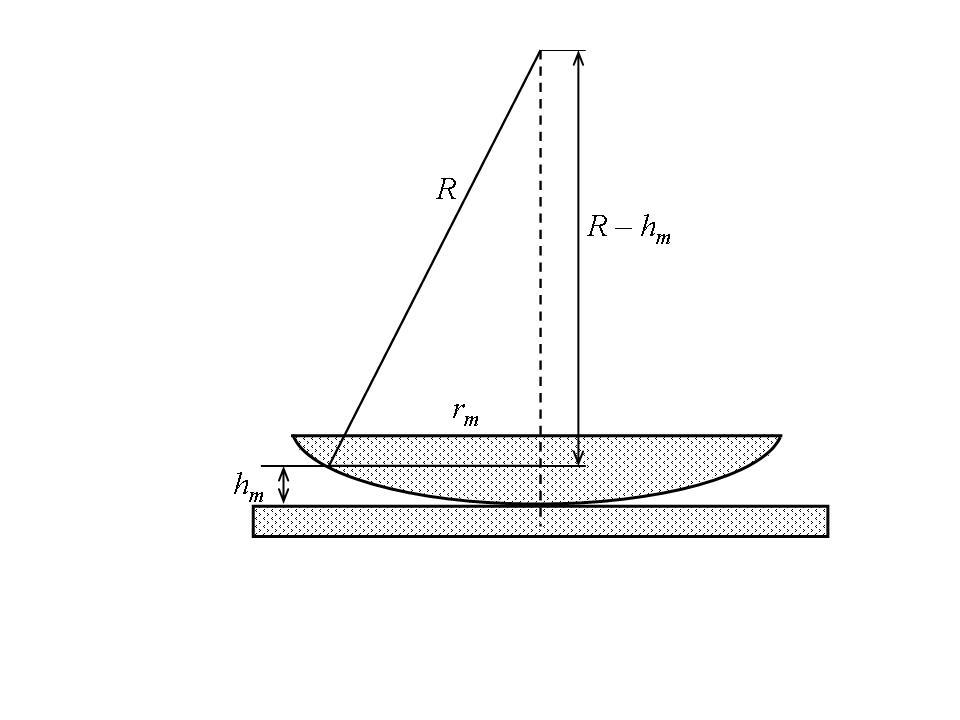
Определим значение h_m. Из рис. 8.4а следует, что

R² = (R – h_m)² + r_m²  R² – 2R h_m + r_m², (8.3)

где R - радиус кривизны линзы, r_m - радиус окружности, всем точкам которой соответствует одинаковый зазор толщиной h_m. Считаем h_m ² < 2R h_m, тогда из (8.3) получим, что h_m = r_m²/2R. Оптическая разность хода лучей окончательно запишется так

 = r_m²/R + _о/2. (8.4)

В точках, для которых  = m'_о ⁼ 2m'(_о/2), наблюдаются максимумы, в точках, для которых

 = (m' + 1/2)_о = (2m'+ 1)(_о/2),

– минимумы интенсивности.

Оба условия можно объединить в одно:

 = m_о/2, (m = 1, 2, 3, …), (8.4а)

причем четным значениям m будут соответствовать максимумы, а нечетным –минимумы интенсивности. Приравняв (8.4) и (8.4а) и разрешив получившееся уравнение относительно r_m, найдем радиусы светлых и темных колец Ньютона:

, (8.5)

Четным значениям m соответствуют радиусы светлых колец, нечетным m - радиусы темных колеи. Значению m =1 соответствует точка касания пластинки и линзы (r_m=0). В этой точке наблюдается минимум интенсивности, обусловленный изменением фазы волны на  при отражении световой волны от стеклянной пластинки.

Измеряя расстояния между полосами интерференционной картины для тонких пластин или радиусы колец Ньютона, можно определить длины волн световых лучей и, наоборот, при известной длине волны _о найти радиус кривизны линзы R.

Интерференцию в опыте Ньютона можно наблюдать и в проходящем свете, причем в данном случае не наблюдается потери полуволны, появляющейся при отражении света от стеклянной пластины. Следовательно, оптическая разность хода для проходящего и отраженного света отличается на ₀/2, т.е. максимумам интерференции в отраженном свете соответствуют минимумы в проходящем, и наоборот.

При освещении оптической системы не монохроматическим, а белым светом наблюдается совокупность смещенных друг относительно друга интерференционных полос (колец), образованных лучами разных длин волн, и интерференционная картина приобретает радужную окраску.