
Из структурной схемы (рисунок 2.38, а) очевидно, что для получения логической схемы синхронного D-триггера со статическим управлением необходимо разработать КС, генерирующую функции S̅n и R̅n такими, чтобы базовый R̅S̅-триггер функционировал как D-триггер. Для построения КС составим таблицу истинности для функций S̅n и R̅n на основе таблицы состояний синхронного D-триггера со статическим управлением и таблицы переходов асинхронного R̅S̅-триггера (таблица 2.12).
Таблица 2.12 – Таблица состояний синхронного D-триггера со статическим управлением, совмещенная с таблицей истинности комбинационной схемы
Логические аргументы |
|
Логические функции |
|
Режим работы |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сn |
Dn |
|
Qn |
Qn+1 |
S̅n |
|
R̅n |
|
0 |
0 |
|
0 |
0 |
1 |
|
X |
|
0 |
0 |
|
1 |
1 |
X |
|
1 |
Хранение |
0 |
1 |
|
0 |
0 |
1 |
|
X |
|
|
|
|
||||||
0 |
1 |
|
1 |
1 |
X |
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
0 |
0 |
1 |
|
X |
Подтверждение 0 |
1 |
0 |
|
1 |
0 |
1 |
|
0 |
Загрузка 0 |
1 |
1 |
|
0 |
1 |
0 |
|
1 |
Загрузка 1 |
1 |
1 |
|
1 |
1 |
X |
|
1 |
Подтверждение 1 |
|
|
|
|
|
|
|
|
|
С помощью карт Карно минимизируем выражения для функций S̅n и R̅n (ри-
сунок 2.39).
|
Dn Qn |
|
|
|
|
|
|
|
|
|
|
|
|
Dn Qn |
|
|
|
|
|
|
|
|||
|
Cn |
00 |
01 |
11 |
|
|
10 |
|
|
Cn |
00 |
|
01 |
11 |
10 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
1 |
|
|
X |
|
X |
|
|
1 |
|
|
0 |
X |
1 |
|
|
1 |
X |
|||||
Sn: |
|
|
|
|
|
|
|
|
|
|
|
|
Rn: |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
1 |
|
1 |
|
|
X |
|
|
0 |
1 |
X |
0 |
|
|
1 |
1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Sn = Cn ˅ Dn |
|
|
|
|
Rn = Cn ˅ Dn |
||||||||||||||||
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
б) |
|
||||||
Рисунок 2.39 - Карты Карно для функций S̅n и R̅n синхронного D-триггера со статическим управлением
131

Выполним необходимые объединения на картах Карно (рисунок 2.39) и запишем результат минимизации в МДНФ, а затем преобразуем полученные выражения в базис И-НЕ.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sn = Cn ˅ Dn = Cn ˅ Dn = Cn · Dn. |
(2.28) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rn = Cn ˅ Dn = Cn ˅ Dn = Cn · Dn. |
(2.29) |
||||||||||||||||
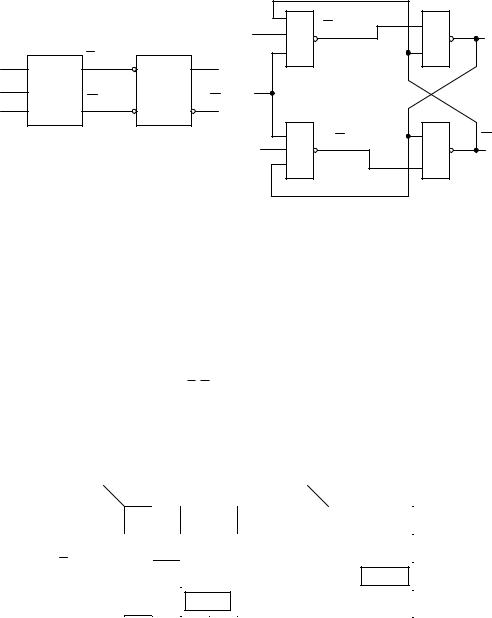
Логическая схема синхронного D-триггера со статическим управлением, построенная по выражениям (2.28) и (2.29) представлена на рисунке 2.38, б. Эта схема может быть упрощена, если при построении КС использовать не минимальное выражение для функции R̅n, а как показано на рисунке 2.40.
|
|
|
|
|
Dn Qn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cn |
00 |
01 |
11 |
10 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
X |
1 |
|
1 |
1 |
|
|
|
|
|
|
||||
|
|
Rn: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
X |
0 |
|
1 |
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rn = Cn ˅ Cn · Dn = Cn ˅ Cn · Dn = Cn · Cn · Dn. |
(2.30) |
||||||||||||||||
Рисунок 2.40 – Карта Карно для функции R̅n синхронного D-триггера со статическим управлением
При использовании для построения триггера выражений (2.28) и (2.30) получается логическая схема синхронного D-триггера со статическим управлением, показанная на рисунке 2.41.
D |
|
|
Sдоп |
Sдоп |
S |
T |
Q |
& |
S |
& |
|
||||
|
|
|
|
||||
|
Q |
|
|
|
|||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
& |
R |
& |
Q |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rдоп |
R |
|
Q |
|
|
|
Rдоп |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
б) |
|
Рисунок 2.41 – Синхронный D-триггер со статическим управлением. Логическая схема (а) и условное графическое обозначение (б)
132
2.2.5 JK-триггеры со статическим управлением
JK-триггер это модернизированный RS-триггер, в котором неопределенное состояние RS-триггера доопределено таким образом, что при J = K = 1 триггер переключается в противоположное состояние. При этом вход J (от англ. Jerk – внезапное включение) соответствует входу S, а вход K (от англ. Kill – внезапное отключение) – входу R.
Рассмотрим синтез JK-триггера со статическим управлением, используя базовый асинхронный R̅S̅-триггер. Структурная схема триггера показана на рисунке 2.42, а.
|
|
|
|
J |
& |
S1 |
& |
Q |
|
|
|
|
|
|
|||
J |
S |
S |
T |
Q |
|
|
|
|
|
|
|
|
|
|
|
||
C |
КС |
|
|
C |
|
|
|
|
|
|
|
Q |
|
|
|
|
|
K |
R |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
& |
R1 |
& |
Q |
|
|
|
|
|
|
а) |
б) |
Рисунок 2.42 – JK-триггер со статическим управлением. Структурная схема (а) и логическая схема (б)
Для синтеза JK-триггера со статическим управлением составим таблицу истинности для функций S̅n и R̅n, используя таблицу состояний JK-триггера и
таблицу переходов асинхронного RS-триггера (таблица 2.13).
На основании таблицы 2.13 заполним карты Карно и минимизируем функции S̅n и R̅n (рисунок 2.43).
|
Jn Kn |
|
|
|
|
Cn Qn |
|
00 |
01 |
11 |
10 |
|
00 |
1 |
1 |
1 |
1 |
|
01 |
X |
X |
X |
X |
Sn: |
11 |
X |
1 |
1 |
X |
|
|||||
|
10 |
1 |
1 |
0 |
0 |
|
Jn Kn |
|
|
|
||
|
Cn Qn |
00 |
01 |
11 |
10 |
|
|
|
|
|
|
|
|
00 |
X |
X |
X |
X |
||
|
|
|
|
|
|
|
|
01 |
1 |
1 |
1 |
1 |
|
Rn: |
|
|
|
|
||
1 |
0 |
0 |
1 |
|||
11 |
||||||
10 |
|
|
|
|
||
X |
X |
1 |
1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sn = Cn ˅ Qn ˅ Jn |
Rn = Cn ˅ Qn ˅ Kn |
||||||||||||
|
|
|
а) |
|
|
|
б) |
||||||
Рисунок 2.43 – Карты Карно для JK-триггера со статическим управлением
133

Таблица 2.13 – Таблица состояний JK-триггера со статическим управлением, совмещенная с таблицей истинности комбинационной схемы
|
Логические аргументы |
|
Логические функции |
Режим работы |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сn |
|
Qn |
Jn |
|
Kn |
Qn+1 |
S̅n |
R̅n |
|
0 |
|
0 |
0 |
|
0 |
0 |
1 |
X |
|
0 |
|
1 |
0 |
|
0 |
1 |
X |
1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
1 |
|
0 |
0 |
1 |
X |
|
0 |
|
1 |
1 |
|
0 |
1 |
X |
1 |
Хранение |
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
0 |
|
1 |
0 |
1 |
X |
|
|
|
|
|||||||
0 |
|
1 |
0 |
|
1 |
1 |
X |
1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
1 |
|
1 |
0 |
1 |
X |
|
0 |
|
1 |
1 |
|
1 |
1 |
X |
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
0 |
|
0 |
0 |
1 |
1 |
Хранение |
1 |
|
1 |
0 |
|
0 |
1 |
X |
X |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
1 |
|
0 |
1 |
0 |
1 |
Загрузка 1 |
1 |
|
1 |
1 |
|
0 |
1 |
X |
1 |
Подтверждение 1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
0 |
|
1 |
0 |
1 |
X |
Подтверждение 0 |
1 |
|
1 |
0 |
|
1 |
0 |
1 |
0 |
Загрузка 0 |
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
1 |
|
1 |
1 |
0 |
1 |
Переключение |
1 |
|
1 |
1 |
|
1 |
0 |
1 |
0 |
(счетный) |
|
|
|
|
|
|
|
|
|
|
Выполним необходимые объединения на картах Карно и запишем результаты минимизации в МКНФ, а затем преобразуем их в базис И-НЕ.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sn = Cn ˅ Qn ˅ Jn = Cn · Qn · Jn |
(2.31) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rn = Cn ˅ Qn ˅ Rn = Cn · Qn · Rn |
(2.32) |
||||||||||||||||
Схема JK-триггера, построенная по выражениям (2.31) и (2.32), показана на рисунке 2.42, б.
Недостатком JK-триггера со статическим управлением (рисунок 2.42, б) является возникновение автоколебательного режима в течение длительности импульса синхронизации из-за наличия обратных связей, если J = K = 1. В результате после окончания импульса синхронизации состояние триггера будет неизвестно. Это говорит о том, что синхронный JK-триггер со статическим управлением не может быть реализован на одной элементарной запоминающей ячейке.
Поэтому практически используемыми JK-триггерами являются:
– двухступенчатые, управляемые синхроимпульсом;
134
– триггеры с динамическим управлением.
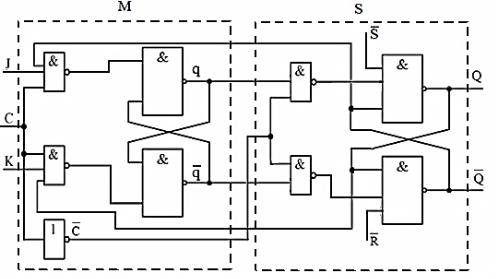
Триггеры, управляемые синхроимпульсом, строят по двухступенчатой конфигурации типа MS (от англ. Master-Slave – «мастер-помощник»). JK-триггер типа MS состоит из двух синхронных RS-триггеров с обратной связью с выхода второго на вход первого (рисунок 2.44).
Рисунок 2.44 – Двухступенчатый JK-триггер с инвертором
Если сигнал С = 1, то первый триггер имеет разрешение на запись информации и состояние выходов q и q̅ зависит от состояния входов J и K. В то же время, на второй триггер подается запрещающий сигнал C̅, поэтому он находится в предыдущем состоянии, т. е. хранит ранее записанную информацию.
Когда значение сигнала С изменяется на низкий уровень (С = 0, C̅ = 1), на первый триггер подается сигнал запрета, а на второй триггер – разрешения. Поэтому выходы Q и Q̅ повторяют состояния на выходах q и q̅первого триггера, т. е. состояние первого триггера переписывается во второй. В этой схеме сигналы обратной связи не меняются в течение действия импульса синхронизации, поэтому двухступенчатый триггер не может находиться в автоколебательном режиме. Поскольку новое состояние триггера появляется на выходе второй ступени при низком уровне сигнала синхронизации (С = 0), то двухступенчатый JK-триггер имеет инверсный статический вход C (рисунок 2.45).
Имеются и другие варианты построения схем двухступенчатых JKтриггеров со статическим управлением. Например, в схеме с запрещающими связями сигналы блокировки второго триггера берутся со входов асинхронного R̅S̅-триггера первой ступени.
135
S TT |
Q |
|
|
J |
|
C |
|
K |
Q |
|
|
R |
|
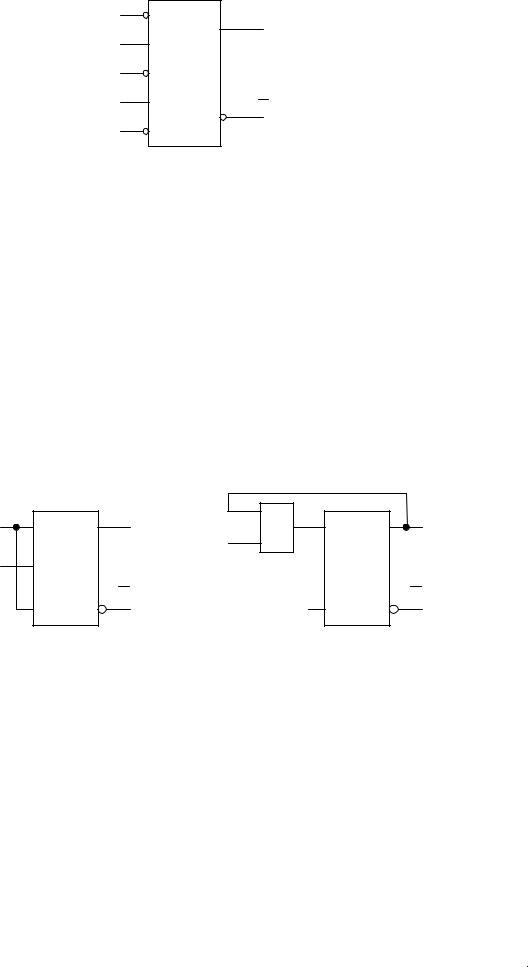
Рисунок 2.45 – Условное графическое обозначение двухступенчатого JK-триггера со статическим управлением
2.2.6 Т-триггеры со статическим управлением
Т-триггер имеет один информационный вход Т (от англ. Toggle – переключатель) и вход синхронизации С. Т-триггер изменяет свое состояние на противоположное каждым импульсом синхронизации, если Т = 1, и сохраняет свое состояние, если Т = 0. Т-триггеры не производятся в интегральном исполнении, так как могут быть легко построены из JK- и D-триггеров.
Исходя из определения Т- и JK-триггеров очевидно, что Т-триггер получается из JK-триггера, если входы J и K объединить (рисунок 2.46, а).
T |
TT |
Q |
=1 |
D TT |
Q |
J |
|
T |
|
||
|
|
|
|
|
|
C |
|
|
|
|
|
K |
|
Q |
|
С |
Q |
|
|
|
|
||
|
а) |
|
|
б) |
|
Рисунок 2.46 – Т-триггер на основе JK-триггера (а) и D-триггера (б)
Для того, чтобы преобразовать D-триггер в Т-триггер, воспользуемся таблицами переходов обоих триггеров (таблица 2.14).
Таблица 2.14 – Таблицы переходов D- и T-триггеров
Текущее состояние |
Следующее состоя- |
D-триггер |
Т-триггер |
|
ние |
||||
|
|
|
||
|
|
|
|
|
Qn |
Qn+1 |
Dn |
Tn |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
|
|
|
|
|
136
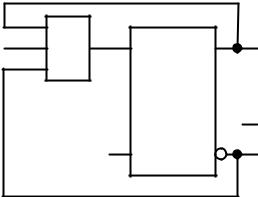
Структурная схема Т-триггера на основе D-триггера показана на рисунке 2.47.
T |
КС D |
С
D TT |
Q |
|
Q
С
Рисунок 2.47 – Т-триггер на основе D-триггера
Из рисунка 2.47 следует, что необходимо синтезировать такую КС, чтобы D- триггер функционировал как T-триггер. Логическая функция, описывающая эту КС, имеет входные переменные Тn и Qn, а выходная переменная – Dn (таблица 2.14). Функция Dn (Qn, Tn) может быть записана в СДНФ по данным таблицы 2.14 в следующем виде:
Dn = Q̅n ∙ Tn ˅ Qn ∙ T̅n = Qn Tn. |
(2.33) |
Схема Т-триггера на основе D-триггера, построенная по выражению (2.33), показана на рисунке 2.46, б. Если сигнал Т = 1, то триггер меняет свое состояние всякий раз, когда поступает импульс синхронизации.
Если переменная Tn в уравнении (2.33) равна единице, то уравнение логично
переписать следующим образом: |
|
Dn = Q̅n. |
(2.34) |
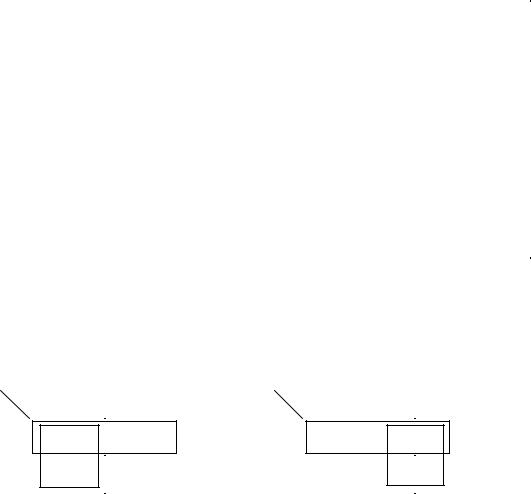
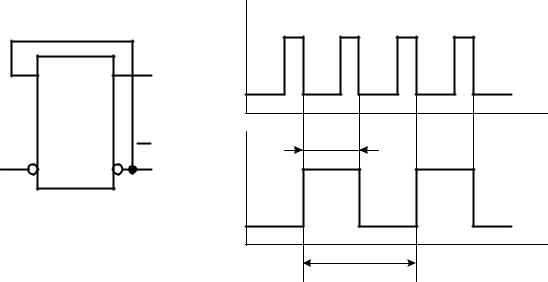
Уравнение (2.34) показывает, что схему делителя частоты на два можно построить простым соединением выхода Q̅ со входом D (рисунок 2.48, а). На рисунке 2.48, б показаны временные диаграммы работы D-триггера в режиме деления частоты.
Необходимо отметить, что Т-триггер может быть построен на основе двухступенчатых триггеров со статическим управлением и синхронных триггеров с динамическим управлением.
137
|
|
|
T |
|
D TT |
Q |
|
|
|
|
|
|
|
|
t |
|
|
|
Tвх |
T |
С |
Q |
Q |
|
|
|
|
|
|
|
t |
|
|
|
Tвых |
|
а) |
|
б) |
Рисунок 2.48 – Схема делителя частоты на два на основе D-триггера (а) и его временные диаграммы (б)
2.2.7 Синхронный D-триггер с динамическим управлением
Смотри в [1].
Контрольные вопросы к теме 2.2
Смотри в [1].
138
Тема 2.3 Регистры памяти и сдвига
2.3.1 Регистры, их назначение и классификация
Регистром называют ПЦУ, предназначенное для приема, хранения, преобразования и передачи информации в другие узлы в процессе выполнения операций в вычислительных устройствах.
Регистр представляет собой совокупность триггеров, число которых соответствует количеству разрядов размещаемых в нем кодовых слов. Наличие прямых и инверсных выходов позволяет использовать регистр для преобразования прямого двоичного кода в обратный и наоборот.
Регистры классифицируются по следующим признакам.
По способу приема и выдачи данных регистры подразделяются на параллельные, последовательные и параллельно-последовательные.
Впараллельных регистрах прием и выдача n-разрядного слова производится по всем разрядам одновременно под воздействием управляющего синхросигнала.
Впоследовательных регистрах прием и выдача n-разрядного слова производится последовательно разряд за разрядом. При этом внутри регистра возможны однонаправленный сдвиг слова из разряда в разряд влево или вправо, а также двунаправленный (реверсивный) сдвиг.
Впараллельно-последовательных регистрах прием и выдача n-разрядных слов могут производиться в последовательном, параллельном и смешанном режимах. В смешанном режиме регистр выполняет функции преобразователя параллельного входного кода в последовательный выходной код либо наоборот.
Регистры можно строить на RS-, D- и JK-триггерах. В современной цифровой схемотехнике регистры обычно строят на D-триггерах с прямым динамическим входом синхронизации, которые обеспечивают простоту схемы и высокое быстродействие. Регистры широко представлены в стандартных сериях цифровых элементов как ИС средней степени интеграции.
2.3.2Параллельные регистры
Впараллельных регистрах схемы разрядов не обмениваются данными между собой. Общими для разрядов обычно являются цепи синхронизации (тактирования), сброса, разрешения приема или выдачи, т. е. цепи управления. При-
139
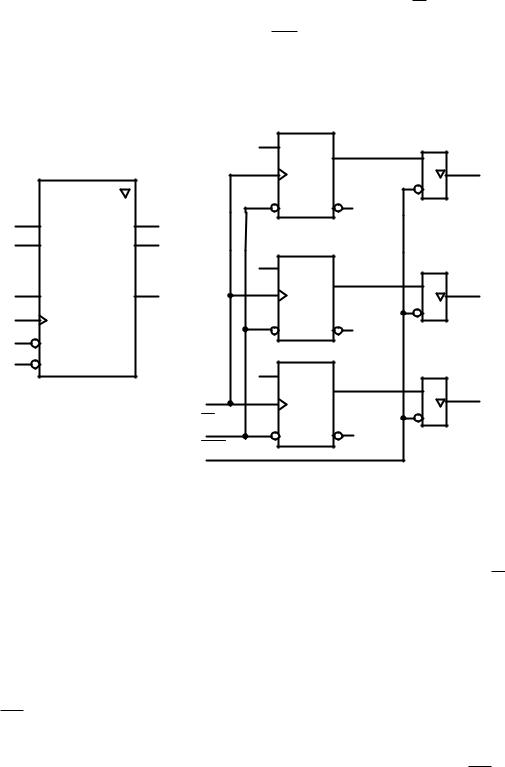
мер схемы параллельного регистра, построенного на D-триггерах с прямым ди-
намическим входом синхронизации, имеющего вход сброса R и выходы с тре-
тьим состоянием, управляемые сигналом OE , показан на рисунке 2.50. УГО регистра представляет собой прямоугольник с аббревиатурой RG (от англ. Register) во внутреннем поле (рисунок 2.50, а).
|
|
Dn-1 |
D T |
1 |
|
|
|
|
C |
Qn-1 |
|
|
|
|
|
||
RG |
|
|
|
|
|
D |
Q |
|
R. |
. . |
|
0 |
0 |
|
. |
. . |
|
1 |
1 |
|
. |
. . |
|
. . |
. |
D1 |
D T |
|
|
. . |
. |
1 |
|
||
. . |
. |
|
C |
Q1 |
|
n-1 |
n-1 |
|
|
||
C |
|
|
R |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
OE |
|
D0 |
D T |
1 |
|
а) |
|
C |
|
Q0 |
|
|
C |
|
|||
|
|
|
|
|
|
|
|
R |
R |
|
|
|
|
OE |
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
Рисунок 2.50 – Параллельный регистр на D-триггерах с прямым динамическим входом синхронизации. Условное графическое обозначение (а) и логическая схема (б)
Для сброса регистра в исходное нулевое состояние на вход сброса R (рисунок 2.50) следует подать нулевой сигнал. Кодовое слово, подлежащее записи в регистр, подается одновременно всеми разрядами на информационные входы Dn-1...D0. Запись входного слова происходит по положительному фронту сигнала синхронизации на входе C. При единичном значении сигнала на входе разрешения OE выходы буферных элементов переходят в третье состояние и регистр работает в режиме хранения. Для выдачи кодового слова на параллель-
ные выходы Qn-1…Q0 подается нулевой сигнал на вход разрешения OE . Выходные буферные элементы (повторители) обеспечивают высокую
нагрузочную способность регистра (рисунок 2.50, б). Это обеспечивает работу регистра непосредственно на шину (магистраль) без дополнительных схем интерфейса, т. е. параллельные регистры могут использоваться в качестве буферных, например, в микропроцессорных устройствах.
140
