
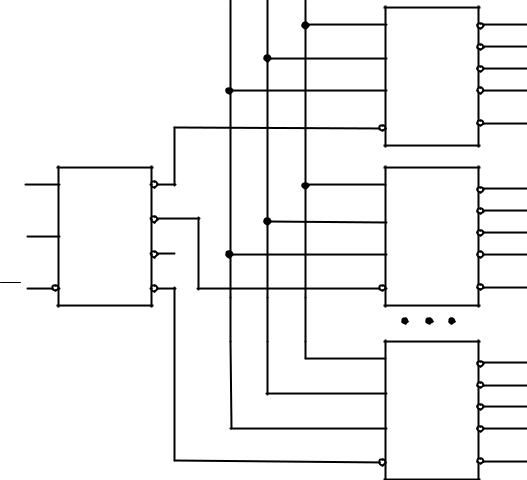
Рисунок 2.4 – Упрощенная логическая схема двухступенчатого дешифратора при n=4
На рисунке 2.5 приведена схема дешифрации пятиразрядного двоичного кода с помощью дешифраторов на три и два входа.
Для получения нужных 32 выходов составляется столбец из четырех дешифраторов «3-8». Дешифратор «2-4» принимает два старших разряда входного слова. Возбужденный нулевой выход этого дешифратора разрешает работу одного из дешифраторов столбца. Выбранный дешифратор столбца расшифровывает три младших разряда входного слова.
|
|
|
x3 |
x4 |
x5 |
|
|
|
|
|
|
0 |
0 |
1 |
|
DC |
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
3-8 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
3 |
|
|
|
|
|
1 |
|
|
... |
|
|
|
|
|
EN |
|
7 |
|
|
|
|
|
|
|
1 |
||
|
|
|
|
|
|
|
|
|
1 |
|
DC |
1 |
|
|
|
DC |
|
|
|
|
|
|
|
|||
x2 |
1 |
2-4 |
0 |
|
|
1 |
0 |
|
|
|
3-8 |
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
2 |
|
2 |
|
|
|
|
|
|
|||
x1 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
4 |
|
3 |
0 |
|
|
0 |
|
1 |
|
|
... |
EN |
|
|
EN |
|
|
|||
EN |
5 |
3 |
|
|
2 7 |
|||
|
|
|
|
|
1 |
1 |
DC |
0 |
|
|
|
|
|
|
3-8 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
4 |
|
3 |
|
|
|
|
|
|
|
||
|
|
|
|
|
0 |
|
|
... |
|
|
|
|
|
EN |
|
|
|
|
|
|
|
|
|
4 |
7 |
|
|
|
|
|
|
|
|
|
|
1
1
1
1
...
1
1
1
1
1
...
1
1
0
1
1
...
1
y0
y1 y2 y3
y7
y8
yy9
10 y11
y
15
y
24
y
25 y26 y27
y
31
Рисунок 2.5 – Схема наращивания разрядности двоичного дешифратора
Каждому входному слову соответствует возбуждение только одного выхода. Например, при дешифрации слова x1x2x3x4x5=11001(2)=25(10) на входы дешифратора первого яруса поступает код 11, возбуждающий его выход номер три, что разрешает работу дешифратора DC4.
На входах DC4 действует код 001, поэтому лог. 0 появится на его первом выходе, т. е. на выходе y25 схемы в целом, что и требуется.
91

Общее разрешение или запрещение работы схемы осуществляется по входу EN дешифратора первого яруса DC5.
92
2.1.4 Шифраторы
Шифратором называется КЦУ, которое преобразует двоичные слова из унитарного кода в позиционный.
Таким образом, шифрация является операцией, обратной дешифрации. При возбуждении одного из входов шифратора на его выходе формируется двоичный код номера возбужденной входной линии. Двоичный шифратор имеет 2n входов и n выходов.
Приоритетные шифраторы выполняют более сложную операцию. При работе ЭВМ и в других устройствах часто решается задача определения приоритетного претендента на использование какого-либо ресурса. Несколько конкурентов выставляют свои запросы на обслуживание, которые не могут быть удовлетворены одновременно. Нужно выбрать того, кому предоставляется право первоочередного обслуживания. Простейший вариант решения указанной задачи – присвоение каждому источнику запросов фиксированного уровня приоритета. Например, группа восьми запросов R7…R0 (R, от англ. Request - запрос) формируется так, что высший приоритет имеет источник R7, а далее уровень приоритета уменьшается от номера к номеру. Самый младший приоритет у источника R0, он будет обслуживаться только при отсутствии всех других запросов. Если имеется одновременно несколько запросов, то обслуживается запрос с наибольшим номером. Приоритетный шифратор вырабатывает на выходе двоичный номер старшего запроса.
Принцип построения двоичных шифраторов рассмотрим на примере синтеза полного шифратора на два выхода (n = 2). УГО такого шифратора представлено на рисунке 2.6.
y0 |
|
0 |
CD |
|
|
|
1 |
|
x2 |
||
y1 |
|
1 |
|
||
|
|
||||
|
|
|
|
||
|
|
|
|
||
y2 |
|
2 |
2 |
|
x1 |
|
|
||||
y3 |
|
3 |
|
||
|
|
||||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
|
|
Рисунок 2.6 – Условное графическое обозначение двоичного шифратора
93
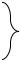
УГО шифратора представляет собой прямоугольник с буквами CD (от англ. Coder) во внутреннем поле. Принцип работы данного двоичного шифратора поясняется следующей таблицей истинности (таблица 2.2).
Таблица 2.2 – Таблица истинности двоичного шифратора
|
Логические аргументы |
|
Логические функции |
||
|
|
|
|
|
|
y0 |
y1 |
y2 |
y3 |
x1 |
x2 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
1 |
|
|
|
|
|
|
0 |
0 |
1 |
0 |
1 |
0 |
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
1 |
|
|
|
|
|
|
Из таблицы 2.2 следует, что логические функции, определяющие работу шифратора, представляют собой дизъюнкции входных аргументов yi ( i = 0,1,2,3), для которых значение функции равно единице, следовательно:
x1 = y2 ˅ y3;
(2.6)
x2 = y1 ˅ y3.
Полученный результат можно распространить на любую функцию, описывающую некоторый двоичный шифратор.
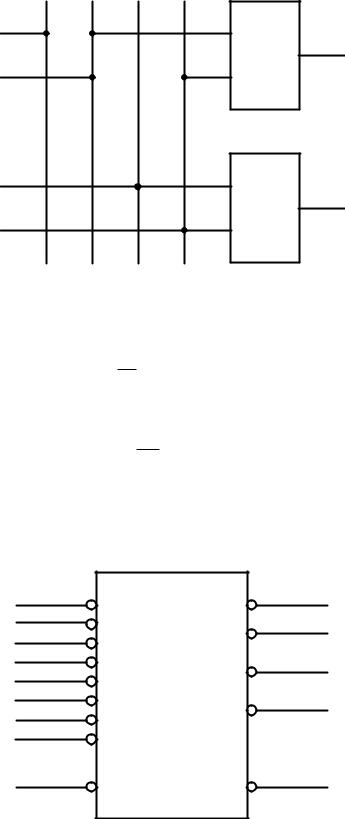
Логическая схема двоичного шифратора, построенная по функциям (2.6), показана на рисунке 2.7.
Всхеме шифратора на рисунке 2.7 проведена проверка правильности функционирования, если возбужден вход y2. Так как на выходах шифратора слово 10, то схема функционирует в соответствии с таблицей истинности (таблица
2.2).
Быстродействие такого шифратора оценивается величиной задержки одного дизъюнктора TCD = tзд. ЛЭ, а затраты оборудования ЕCD = 4 условных транзистора.
Если шифратор имеет инверсные входы, то возбужденный вход имеет нулевое значение, а все остальные – единичное.
Всериях интегральных микросхем стандартной логики имеются приоритетные шифраторы восьмиразрядных и десятиразрядных слов. Например, микросхема К555ИВ1 схемотехники ТТЛШ содержит приоритетный шифратор «8-3» (рисунок 2.8).
94
|
y0 |
y1 |
y2 |
y3 |
|
|
y0 |
0 |
|
|
0 |
1 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
x2 |
|
|
0 |
|
|
0 |
|
|
y1 |
|
|
|
|
||
|
|
|
|
|
|
1 |
1 |
1 |
|
y2 |
|
1 |
|
|
|
x1 |
|
0 |
0 |
|
|
|
|
||
y3 |
|
|
|
Рисунок 2.7 – Логическая схема двоичного шифратора
Шифратор К555ИВ1 имеет инверсные информационные входы y0 … y7 и выходы x1, x2, x3, т. е. на выходах формируется обратный код. Нулевое значение сигнала на разрешающем входе EI (от англ. Enable Input) разрешает работу данного шифратора, а единичное – запрещает. Нулевое значение сигнала на выходе G отмечает наличие возбужденного входа у данного шифратора. Нулевое значение сигнала на выходе EO (от англ. Enable Output) вырабатывается при отсутствии возбужденных входов у данного шифратора для разрешения работы следующего (младшего) шифратора при соединении нескольких микросхем с целью наращивания числа входов и выходов.
y0 |
0 |
CD |
G |
|
|
|
|||
y1 |
|
|
||
1 |
|
|
|
|
y2 |
|
1 |
x3 |
|
2 |
|
|||
|
|
|
|
|
y3 |
3 |
|
|
x2 |
y4 |
|
2 |
||
4 |
|
|||
y5 |
|
|
|
|
5 |
|
|
x1 |
|
y6 |
|
4 |
||
6 |
|
|||
y7 |
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
EI |
|
EO |
|
Рисунок 2.8 – Условное графическое обозначение микросхемы приоритетного шифратора К555ИВ1
95
2.1.5 Преобразователи кодов
Преобразователем кодов (ПК) называют КЦУ, которое преобразует n- разрядные двоичные входные слова в m-разрядные двоичные выходные слова. Иногда ПК называют n, m-преобразователями. Рассмотренные ранее дешифраторы и шифраторы являются ПК некоторых частных видов, например, их можно использовать для преобразования чисел из одной позиционной системы счисления в другую.
Для представления информации, в цифровых устройствах используются двоичные коды. Например, двоично-десятичный код 8421 (BCD-код) используется для представления десятичных чисел. Двоично-десятичный код с избытком 3, также используемый для представления десятичных цифр, образуется от соответствующих представлений цифр в коде 8421 путем прибавления двоичного числа 0011. Код с избытком 3 является самодополняющим кодом. Правила преобразования прямого кода с избытком 3 в дополнительный с избытком 3 и правила обратного преобразования такие же, как и для двоичного дополнительного кода. Поэтому код с избытком 3 удобнее использовать для выполнения арифметических операций.
Построение схемы ПК рассмотрим на конкретном примере. Пусть требуется построить преобразователь четырехразрядных двоично-десятичных цифр из кода 8421 в код с избытком 3. УГО такого ПК представлено на рисунке 2.9.
x0 |
|
1 |
X/Y 0 |
|
y0 |
|
|
||||
x1 |
|
2 |
1 |
|
y1 |
|
|
||||
|
|||||
x2 |
|
4 |
2 |
|
y2 |
|
|
||||
x3 |
|
8 |
3 |
|
y3 |
|
|
||||
|
|
|
|
|
|
Рисунок 2.9 – Условное графическое обозначение преобразователя кода 8421 в код с избытком 3
Соотношение входных и выходных слов задано таблицей истинности (таб-
лица 2.3).
96
Таблица 2.3 – Таблица истинности преобразователя кода 8421 в код с избытком 3
|
Логические аргументы |
|
Промежуточная пе- |
|
Логические функции |
|
||||||
|
|
ременная |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
x2 |
x1 |
|
x0 |
zi |
y3 |
|
y2 |
y1 |
|
y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
0 |
|
0 |
z0 |
0 |
|
0 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
0 |
|
1 |
z1 |
0 |
|
1 |
0 |
|
0 |
0 |
|
0 |
1 |
|
0 |
z2 |
0 |
|
1 |
0 |
|
1 |
0 |
|
0 |
1 |
|
1 |
z3 |
0 |
|
1 |
1 |
|
0 |
0 |
|
1 |
0 |
|
0 |
z4 |
0 |
|
1 |
1 |
|
1 |
0 |
|
1 |
0 |
|
1 |
z5 |
1 |
|
0 |
0 |
|
0 |
0 |
|
1 |
1 |
|
0 |
z6 |
1 |
|
0 |
0 |
|
1 |
0 |
|
1 |
1 |
|
1 |
z7 |
1 |
|
0 |
1 |
|
0 |
1 |
|
0 |
0 |
|
0 |
z8 |
1 |
|
0 |
1 |
|
1 |
1 |
|
0 |
0 |
|
1 |
z9 |
1 |
|
1 |
0 |
|
0 |
Имея таблицу истинности, можно использовать три подхода к синтезу ПК:
–преобразователь синтезируется как однокомпонентная минимизированная комбинационная схема с нерегулярной структурой (по общим правилам синтеза КЦУ);
–преобразователь синтезируется как слабо минимизированная комбинационная схема с частично регулярной структурой (на основе шифратора и дешифратора);
–преобразователь синтезируется как неминимизированная комбинационная схема с регулярной структурой (на основе постоянного запоминающего устройства).
Рассмотрим первый традиционный подход. По данным таблицы 2.3 заполним карты Карно (рисунок 2.10).
X1 X0 |
|
|
|
X1 X0 |
|
|
|
||
X3 X2 |
00 |
01 |
11 |
10 |
X3 X2 |
00 |
01 |
11 |
10 |
|
|
|
|
|
|
|
|
||
00 |
0 |
0 |
0 |
0 |
00 |
0 |
1 |
1 |
1 |
01 |
0 |
1 |
1 |
1 |
01 |
1 |
0 |
0 |
0 |
11 |
Ф |
Ф |
Ф |
Ф |
11 |
Ф |
Ф |
Ф |
Ф |
10 |
1 |
1 |
Ф |
Ф |
10 |
0 |
1 |
Ф |
Ф |
y3 = x3 ˅ x0 · x2 ˅ x1 · x2. |
y2 = x0 · x1 · x2 ˅ x0 · x2 ˅ x1 · x2. |
||||||||
Рисунок 2.10 – Карты Карно для преобразователя кода 8421 в код с избытком 3
97
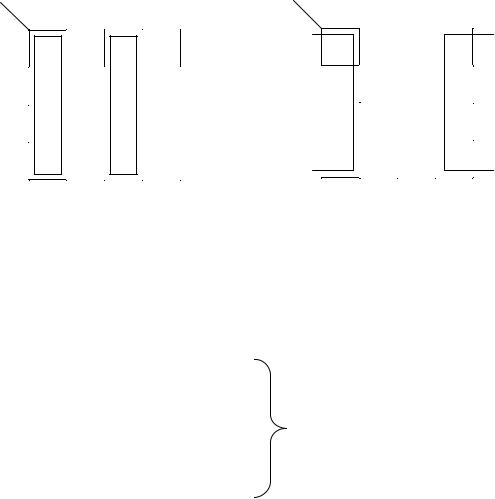
X1 X0 |
|
|
|
|
X3 X2 |
00 |
01 |
11 |
10 |
|
|
|
|
|
00 |
1 |
0 |
1 |
0 |
01 |
1 |
0 |
1 |
0 |
11 |
Ф |
Ф |
Ф |
Ф |
10 |
1 |
0 |
Ф |
Ф |
|
y1 = x0 · x1 ˅ x0 · x1. |
|||
X1 X0 |
|
|
|
|
X3 X2 |
00 |
01 |
11 |
10 |
|
|
|
|
|
00 |
1 |
0 |
0 |
1 |
01 |
1 |
0 |
0 |
1 |
11 |
Ф |
Ф |
Ф |
Ф |
10 |
1 |
0 |
Ф |
Ф |
|
|
y0 = x0. |
|
|
Окончание рисунка 2.10
Выполним соответствующие объединения заполненных клеток на рисунке 2.10 с учетом неопределенностей и запишем результаты минимизации в МДНФ:
y3 = x3 ˅ x0 · x2 ˅ x1 · x2;
y2 = x0 · x1 · x2 ˅ x0 · x2 ˅ x1 · x2;
(2.7)
y1 = x0 · x1 ˅ x0 · x1;
y0 = x0.
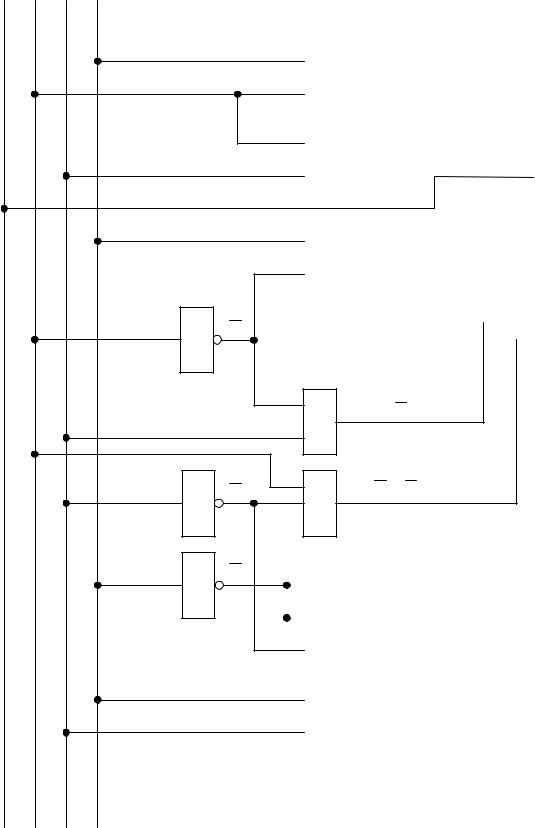
Далее по функциям системы (2.7) методом прямого замещения построим логическую схему ПК в основном базисе (рисунок 2.11).
На рисунке 2.11 проведена проверка правильности функционирования схемы для входного слова 0011. Так как на выходах схемы установилось выходное слово 0110, то ПК функционирует в соответствии с таблицей 2.3.
Кдостоинству первого подхода относится экономичность синтезируемой схемы по аппаратурным затратам, исчисляемым в условных транзисторах. Это означает, что схема будет занимать небольшую часть площади кристалла. Оценка схемы на рисунке 2.11 дает величину ЕПК (1) = 26 условных транзистора.
Кнедостатку этого подхода можно отнести то, что схема получилась нерегулярной (с неравным числом конъюнкторов в цепи каждого выхода, с перекрещивающимися связями), что делает ее нетехнологичной при изготовлении.
98
X3 X2 X1 X0
0 0 1 1
1 X2
1
1 X1
0
1 X0
0
& |
X0 |
· X2 |
|
|
|
|
|||||
|
|
|
|
|
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
1 |
|
|
|
X1 |
· X2 |
0 |
|
y3 |
|||||||
|
|
|
|||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
X0 |
· X2 |
|
|
|
|
||||||
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
y2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
&X1 · X2 1
&X0 · X1 · X2
0
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
X0 · X1 |
|
|
|
|
||||||
|
|
|
|
|
|||||||
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
y1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
X0 · X1 |
|
|
|
|
|
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
y0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2.11 – Логическая схема ПК 8421 в код с избытком 3 в основном базисе
99
Второй подход позволяет повысить регулярность структур ПК за счет некоторого увеличения аппаратурных затрат. Исходная информация для синтеза в том случае также содержится в таблице 2.3, в которой имеется столбец с промежуточной переменной zi (при первом подходе этот столбец не учитывался).
Левая и центральная части таблицы 2.3 представляют собой описание дешифратора, а правая и центральная части представляют собой таблицу кодирования некоторого шифратора. Таким образом, схема ПК в данном случае приобретает двухкомпонентную структуру вида «десятичный дешифраторшифратор» (рисунок 2.12). Она несколько сложнее схемы на рисунке 2.11 (ЕПК(2)=77 условных транзисторов), но значительно проще для обозрения.
К недостатку полученной схемы следует отнести ее специализированность, что снижает массовость выпуска подобных схем и приводит к относительно высокой цене изделия.
x0 |
|
1 |
DC |
0 |
|
0 |
CD |
0 |
|
y0 |
|
|
|
||||||||
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3 |
|
3 |
|
|
|
|
x1 |
2 |
|
|
|
1 |
|
y1 |
|||
|
|
|
|
|
|
|||||
|
|
|
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x2 |
|
4 |
|
5 |
|
5 |
|
2 |
|
y2 |
|
|
|
|
|
||||||
|
|
6 |
|
6 |
|
|
||||
|
|
|
|
|
||||||
|
|
|
||||||||
|
|
|
|
7 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x3 |
|
8 |
|
8 |
|
8 |
|
3 |
|
y3 |
|
|
|
|
|
||||||
|
|
9 |
|
9 |
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2.12 – Преобразователь кода с частично регулярной структурой
Третий подход позволяет значительно повысить регулярность структуры ПК и одновременно существенно расширить его функциональные возможности. В этом случае запрещается использовать специализированные компоненты, например, десятичный дешифратор. Таким образом, ПК должен содержать полный двоичный n-входной дешифратор и 2n-входной шифратор. В результате получается постоянное запоминающее устройство (ПЗУ). Следовательно, ПЗУ
– это n, m-преобразователь с двухкомпонентной регулярной структурой, на выходе которого включен шифратор, формирующий m-разрядные слова.
Входное слово ПК в этом случае является адресом ячейки ПЗУ, в которой хранится соответствующее выходное слово. УГО ПК на ПЗУ представлено на
100
