Archive / Конспект лекций от 02.04.12 - копия / УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА 3

4

ИЗОПРОЦЕССЫ.

УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА.

1.Изопроцессы. Графики изопроцессов.

а) Изотермический процесс.

Закон Бойля-Мариотта.

При постоянной массе газа и неизменной температуре произведение давления газа на его объём есть величина постоянная.

PV=const или P₁V₁=P₂V₂ или

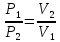
б) Изобарный процесс.

Закон Гей-Люссака.

С введением абсолютной термодинамической шкалы запись этого закона упрощается.

При постоянной массе газа и неизменном давлении отношение объёма газа к его температуре постоянно.

в) Изохорный процесс.

Закон Шарля.

С введением абсолютной термодинамической шкалы запись этого закона упрощается.

При постоянной массе газа и неизменном объёме отношение давления газа к его температуре постоянно.

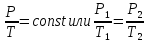
2.Уравнение состояния идеального газа или уравнение Клапейрона.

Покажем, что для двух состояний одной и той же массы газа можно записать: =

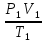Переведём газ из состояния P₁ V₁ T₁ в состояние P₂ V₂ T₂ через промежуточное состояние P₃ V₃ T₃.

Нагреем газ изобарно (переход 1-3). Для этого процесса можно записать:

=

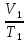Так как Р₁=Р₃, то умножим левую часть равенства на Р₁, а правую на Р₃. =

Сожмём газ изотермически (переход 3-2).

Так как P₃V₃=P₂V₂, а Т₃=Т₂, то P₃V₃ заменим на P₂V₂, а Т₃ на Т₂. Получим:

= или

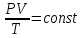
Это уравнение состояния идеального газа или уравнение Клапейрона.

При любом изменении состояния данного количества газа произведение давления на объём, делённое на абсолютную температуру, остаётся постоянным.

3.Уравнение Клапейрона-Менделеева.

Если газ находится под давлением Р₀ = 1 атм. = 1,013 10⁵ Па = 760 мм рт.ст. и при температуре Т₀ =273 К ( t⁰ = 0⁰C), то говорят, что газ находится при нормальных условиях (н.у.).

По закону Авогадро 1 моль газа при н.у. занимает объём V₀ = 22,4 л = =22, 4 10^-3 м^-3. Тогда для одного моля

На основании уравнения Клапейрона, можно утверждать, что для любого состояния одного моля идеального газа верно равенство

, где R=8,31 - универсальная газовая постоянная.

Следовательно PV = RT.

Д.И.Менделеев показал, что для ν молей

PV = νRT или

Это уравнение Клапейрона-Менделеева.

4.Температура – мера средней кинетической энергии движения молекул.

Уравнение Клапейрона-Менделеева позволяет получить ещё одну (четвёртую) формулировку основного уравнения МКТ.

Для этого, используя уравнение Клапейрона-Менделеева выразим давление

= = = nkT,

где = 1,38 10^-23 Дж/К – постоянная Больцмана.

Итак, – четвёртая формулировка основного уравнения МКТ.

Сравним это выражение со второй формулировкой . Тогда

и

= kT или

Отсюда видно, что температура – это величина, которая характеризует среднюю кинетическую энергию поступательного движения молекул идеального газа.

Последние выражения позволяют установить зависимость между среднеквадратичной скоростью поступательного движения молекул газа и его температурой.

По определению 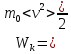, где – масса одной молекулы. Следовательно,

= kT и

=

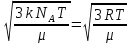
5.Закон Дальтона.

Если в сосуде имеется смесь из двух или более химически не взаимодействующих газов, то давление смеси равно сумме парциальных давлений этих газов.

Парциальным называется давление, которое оказывал бы газ на стенки сосуда, если бы находился в этом сосуде один.

Допустим, что смесь состоит из n газов. Тогда давление смеси

+…+

Где Р₁, Р₂ … Р_n – парциальные давления газов.