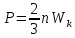Archive / Конспект лекций от 02.04.12 - копия / Идеальный газ. МКТ 1

4

МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА.

МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ.

ИДЕАЛЬНЫЙ ГАЗ. ОСНОВНОЕ УРАВНЕНИЕ МКТ.

1.Молекулярно-кинетическая теория.

Атомы имеют сложное строение, но классическая молекулярно-кинетическая теория рассматривает их как твёрдые неделимые частицы сферической формы, взаимодействующие друг с другом по законам классической механики. Это физическая модель атома.

Основные положения молекулярно-кинетической теории.

1. Все вещества состоят из мельчайших частиц – молекул (простейшие молекулы состоят из одного атома), которые находятся на определённых расстояниях друг от друга.

Доказательства – сжимаемость, диффузия.

2. Молекулы находятся в непрерывном хаотическом тепловом движении.

Доказательства – диффузия, броуновское движение.

3. Молекулы связаны друг с другом силами молекулярного взаимодействия, которые в зависимости от расстояния между молекулами являются либо силами отталкивания, либо силами притяжения.

Доказательства – трудность сжатия или растяжения твёрдых и жидких тел.

Вопрос: почему теория называется молекулярно-кинетической?

2.Относительная молекулярная (атомная) масса.

Поскольку массы атомов и молекул малы, то удобнее при расчётах в качестве единицы массы использовать не килограмм, а атомную единицу массы.

Атомной единицей массы назвали 1/12 часть массы атома углерода, т.е. 1 а.е.м.= 1/12 m_0С= 1,66 10^-27 кг.

Относительной молекулярной (атомной) массой называется отношение массы молекулы m₀ данного вещества к атомной единице массы.

Приблизительную атомную массу веществ можно определить по таблице Менделеева.

3.Количество вещества. Постоянная Авогадро.

Количество вещества, содержащегося в физическом теле, определяется числом молекул (атомов) в этом теле. Поскольку число молекул в макроскопическом теле очень велико, то количество вещества удобнее считать не отдельными молекулами, а порциями, каждая из которых содержит вполне определённое число молекул. Такая порция молекул называется один моль вещества.

1 моль – это количество вещества, содержащее столько же молекул (атомов), сколько содержится атомов в 12 г углерода ₆¹²С.

В одном моле содержится 6,02 10²³ молекул (атомов). Это число называется числом Авогадро.

N_А=6,02 10²³ моль^-1.

Количество вещества ν – это количество молей, содержащихся в веществе.

Масса одного моля называется молярной массой и обозначается буквой μ (мю).

Количество вещества ν можно найти следующим образом:

или

где m – масса вещества, N – количество молекул в этом веществе.

μ=M_r 10^-3

4.Идеальный газ.

Вещество может находиться в трёх агрегатных состояниях – газообразном, жидком и твёрдым. Переход из одного состояния в другое называется фазовым переходом. Рассмотрим самое простое из этих состояний – газообразное.

Опыт показывает, что газ собственной формы не имеет, а равномерно заполняет весь доступный ему объём. Молекулы газа могут двигаться в пространстве в самых различных направлениях, периодически сталкиваясь с другими молекулами или со стенками сосуда. На основании I-го закона Ньютона, между столкновениями молекулы движутся равномерно и прямолинейно. При столкновении направление и величина скорости молекул меняется. Получается, что молекулы совершают хаотическое движение. Это послужило причиной того, что данное состояние вещества назвали газом, что означает «хаос».

При атмосферном давлении и температуре 0⁰С среднее расстояние между молекулами ~10 нм, что гораздо меньше радиуса межмолекулярного взаимодействия (~ 1 нм). Следовательно, взаимодействие молекул газа друг с другом при обычных условиях можно не учитывать, за исключением моментов столкновения молекул, когда между ними действуют силы отталкивания.

Этот факт немецкий физик Клаузиус в середине XIX века использовал для создания модели так называемого «идеального газа».

Идеальный газ – это газ со следующими свойствами:

1. Размеры молекул малы по сравнению со средним расстоянием между ними; молекулы можно принять за материальные точки;

2. Силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях;

3. Молекулы сталкиваются друг с другом как абсолютно упругие шары, движение которых описывается законами классической механики (в этом случае принимать молекулы за материальные точки нельзя).

На основании этой модели можно объяснить, почему газ занимает весь предоставленный ему объём, лёгкую сжимаемость газов, давление, которое оказывает газ на стенки сосудов, газовые законы.

Как и любая модель, модель идеального газа имеет свои ограничения. Она применима при небольших давлениях (менее 100 атм) и не очень низких температурах.

5.Характеристики газа.

Для описания состояния газа можно воспользоваться микропараметрами. Это – масса и скорость молекул, энергия и импульс молекул, их концентрация. Данные параметры являются индивидуальными характеристиками молекул. Найти их с помощью простых измерительных приборов невозможно. Гораздо большую практическую роль играют макропараметры. Значения макропараметров определяются совместным действием огромного количества молекул, и измерить их можно, используя достаточно простые приборы.

Три макропараметра – объём, давление и температура – позволяют описать состояние любой газовой системы.

Под объёмом газа понимают объём сосуда, в котором находится газ.

Единица измерения объёма в системе СИ – 1 м³.

Давление газа – это средняя сила ударов молекул о стенки сосуда, приходящаяся на единицу поверхности стенки.

Единица измерения давления в системе СИ – 1 паскаль.

1 паскаль – это давление, при котором на площадь поверхности 1 м² действует сила в 1 Н, направленная перпендикулярно поверхности.

Внесистемная единица измерения давления – физическая атмосфера.

1 атм=10⁵ Па

5.Основное уравнение молекулярно-кинетической теории (МКТ).

Это уравнение связывает микропараметры газа с его макропараметрами.

1. n m₀<v²> ,

где n – концентрация молекул газа, m₀ – масса одной молекулы,

= - усреднённое значение квадрата скорости молекул.

Так как кинетическая энергия молекулы , то

2. 

Обозначим объём газа через V, общее количество молекул через N, а плотность газа ρ. Тогда, учитывая, что , можно записать

(3)

Получили три формулировки основного уравнения МКТ.