
- •Кратные интегралы Задачи, приводящие к двойным интегралам. Определение двойного интеграла
- •Свойства двойного интеграла
- •Вычисление двойного интеграла в прямоугольных декартовых координатах
- •Вычисление двойного интеграла в полярной системе координат
- •Тройной интеграл
- •Криволинейные интегралы второго рода Задача о вычислении работы переменной силы. Определение криволинейного интеграла второго рода
- •Криволинейный интеграл второго рода в координатной форме
- •Вычисление криволинейных интегралов второго рода
- •Формула Грина
- •Условия независимости криволинейного интеграла от пути интегрирования
- •Литература
- •«Высшая математика»
Криволинейные интегралы второго рода Задача о вычислении работы переменной силы. Определение криволинейного интеграла второго рода
Напомним, что если сила
![]() постоянна (по величине и по направлению),
а путь
постоянна (по величине и по направлению),
а путь![]() прямолинеен, то работа этой силы на
заданном пути равна скалярному
произведению векторов
прямолинеен, то работа этой силы на
заданном пути равна скалярному
произведению векторов![]() и
и![]() :
:![]() .
.
Пусть переменная сила
![]() действует вдоль кривой
действует вдоль кривой![]() ,
меняясь при этом в каждой точке приложения
как по модулю, так и по направлению, т.е.
,
меняясь при этом в каждой точке приложения
как по модулю, так и по направлению, т.е.![]() ,
где
,
где![]() ,
,![]() ,
,![]() ― непрерывные вдоль данной кривой
функции. При перемещении материальной
точки вдоль данной кривой
― непрерывные вдоль данной кривой
функции. При перемещении материальной
точки вдоль данной кривой![]() сила
сила![]() совершает некоторую работу
совершает некоторую работу![]() .
.
Чтобы найти эту работу разобьем
произвольным образом кривую на![]() частей
частей![]() ,
,![]() длиной
длиной![]() .В каждой части
.В каждой части![]() выберем произвольным образом точку
выберем произвольным образом точку![]() ,
лежащую на кривой
,
лежащую на кривой![]() .
Пусть
.
Пусть![]() ― единичный вектор касательной к кривой
― единичный вектор касательной к кривой![]() в точке
в точке![]() .
Тогда вместо участка
.
Тогда вместо участка![]() можно приближенно рассматривать вектор
можно приближенно рассматривать вектор![]()
![]() ,
равный ему по длине и приблизительно
по направлению, учитывая направление
вдоль кривой.
,
равный ему по длине и приблизительно
по направлению, учитывая направление
вдоль кривой.

Следовательно, ( если считать силу
![]() (
(![]() )
постоянной на участке
)
постоянной на участке![]() )
элементарная работа
)
элементарная работа![]() силы
силы![]() на участке
на участке![]() приближенно равна скалярному произведению:
приближенно равна скалярному произведению:
![]()
![]() .
.
Вся работа силы
![]() на криволинейном пути
на криволинейном пути![]() приближенно выражается формулой
приближенно выражается формулой
![]()
![]() .
.
Переходя к пределу при
![]() ,
где
,
где![]() ― длина наибольшей из элементарных дуг
― длина наибольшей из элементарных дуг![]() ,
получаем точное значение работы
,
получаем точное значение работы
![]()
![]() .
.
Если данная интегральная сумма имеет
предел при
![]() ,
то он называется криволинейным интегралом
второго рода от вектор - функции
,
то он называется криволинейным интегралом
второго рода от вектор - функции![]() по кривой
по кривой![]() и
обозначается
и
обозначается
![]() .
.
Таким образом, с механической точки зрения криволинейный интеграл второго рода есть работа переменной силы вдоль некоторой линии перемещения.
![]()
![]() .
.
Отметим также, что определение
криволинейного интеграла второго рода
остается в силе и когда кривая
![]() замкнутая. В этом случае начальная и
конечная точки совпадают. Криволинейный
интеграл второго рода по замкнутому
контуру
замкнутая. В этом случае начальная и
конечная точки совпадают. Криволинейный
интеграл второго рода по замкнутому
контуру![]() обозначается следующим образом:
обозначается следующим образом:
![]() .
.
Отметим два свойства криволинейного интеграла.
Свойство 1.Криволинейный интеграл определяется подынтегральным выражением, формой кривой интегрирования и указанием направления интегрирования. При изменении направления интегрирования криволинейный интеграл меняет знак на противоположный.
Свойство 2.Разобьем кривую
интегрирования![]() точкой
точкой![]() на части
на части![]() и
и![]() ,
тогда
,
тогда
![]()
![]()
![]() .
.
Криволинейный интеграл второго рода в координатной форме
При определении криволинейного интеграла
второго рода элементарная работа
![]() силы
силы![]() на участке
на участке![]() находилась как скалярное произведение
вектора
находилась как скалярное произведение
вектора![]() и вектора, приближенно равного по длине
и направлению участку
и вектора, приближенно равного по длине
и направлению участку![]() .
Вместо вектора
.
Вместо вектора![]()
![]() ,
в качестве вектора, близкого к
,
в качестве вектора, близкого к![]() можно взять вектор
можно взять вектор![]() , начало и конец которого совпадают с
началом и концом участка
, начало и конец которого совпадают с
началом и концом участка![]() .
.

Найдем скалярное произведение векторов
![]() и
и![]()
![]() в координатной форме как сумму произведений
соответствующих координат:
в координатной форме как сумму произведений
соответствующих координат:
![]()
![]()
![]()
Переходя к пределу при
![]() ,
где
,
где![]() ― длина наибольшей из элементарных дуг
― длина наибольшей из элементарных дуг![]() ,
получаем точное значение работы
,
получаем точное значение работы
![]()
![]() .
.
Следовательно, криволинейный интеграл второго рода в скалярной координатной форме имеет вид:
![]()
![]()
или, в более краткой форме
![]()
![]() .
.
Вычисление криволинейных интегралов второго рода
Пусть линия
![]() задана параметрически
задана параметрически
![]() :
:
![]() .
.
Тогда по определению дифференциала

Отметим начало дуги
![]() точкой
точкой![]() ,
конец — точкой
,
конец — точкой![]() .
В этом случае говорят, что задано
направление перемещения по кривой от
точки
.
В этом случае говорят, что задано
направление перемещения по кривой от
точки![]()
![]() к точке
к точке![]()
![]() и тем самым указано направление
ориентирующего вектора
и тем самым указано направление
ориентирующего вектора![]() .
.
Покажем, что вычисление криволинейного
интеграла второго рода по линии
![]() заданной параметрически, сводится к
вычислению однократного определенного
интеграла по параметру
заданной параметрически, сводится к
вычислению однократного определенного
интеграла по параметру![]() :
:
![]()
![]()


А в случае плоской кривой, когда
![]() ,
последняя формула примет вид:
,
последняя формула примет вид:
![]()

Замечание.Для плоской кривой,
заданной уравнением![]() ,
,![]() криволинейный интеграл второго рода в
координатной скалярной форме сводится
к определенному интегралу по переменной
криволинейный интеграл второго рода в
координатной скалярной форме сводится
к определенному интегралу по переменной![]()
![]()
![]()
![]()
(Выбрана ориентация
![]() ,
при которой
,
при которой![]() ,
,![]() соответствуют началу и окончанию пути
интегрирования.)
соответствуют началу и окончанию пути
интегрирования.)
Если кривая
![]() задана уравнением
задана уравнением![]() ,
,![]() ,
то при соответствующей ориентации
интегрирование по переменной
,
то при соответствующей ориентации
интегрирование по переменной![]() будет осуществляться от
будет осуществляться от![]() до
до![]() :
:
![]()
![]() .
.
Пример. Вычислить![]() ,
где
,
где![]() —
отрезок прямой с началом в точке
—
отрезок прямой с началом в точке![]() и концом в точке
и концом в точке![]() .
.
Решение. Изобразим на рисунке линию интегрирования.

Воспользуемся формулами параметрических
уравнений прямой с направляющим
вектором
![]() ,
проходящей через начальную точку с
координатами
,
проходящей через начальную точку с
координатами![]() :
:

Запишем параметрические уравнения
прямой, которой принадлежит отрезок
![]() ,
приняв за направляющий вектор прямой
,
приняв за направляющий вектор прямой![]() вектор
вектор![]() .
.
![]() .
.
Начальной точкой отрезка
![]() является
точка
является
точка![]() .
Следовательно, параметрические уравнения
этой прямой:
.
Следовательно, параметрические уравнения
этой прямой:

Из полученных уравнений находим, что
точке
![]() соответствует значение параметра
соответствует значение параметра![]() ,
а точке
,
а точке![]() значение
значение![]() .
.
По определению дифференциала


Подставляя в интеграл значения
![]() и
и![]() ,
а также учитывая значения параметра
,
а также учитывая значения параметра![]() и
и![]() ,
соответствующие началу и концу дуги
,
соответствующие началу и концу дуги![]() ,
получим:
,
получим:
![]()
![]()
![]()
![]() .
.
Пример. Вычислить![]() ,
где
,
где![]() —
отрезок прямой с началом в точке
—
отрезок прямой с началом в точке![]() и концом в точке
и концом в точке![]() .
.
Решение. Изобразим на рисунке линию интегрирования.

![]()
Воспользуемся формулами параметрических
уравнений прямой с направляющим
вектором
![]() ,
проходящей через начальную точку с
координатами
,
проходящей через начальную точку с
координатами![]() :
:

Запишем параметрические уравнения
прямой, которой принадлежит отрезок
![]() ,
приняв за направляющий вектор прямой
,
приняв за направляющий вектор прямой![]() вектор
вектор![]() ,
т. е.
,
т. е.![]() .
.
Начальной точкой отрезка
![]() является
точка
является
точка![]() .
Следовательно, параметрические уравнения
этой прямой:
.
Следовательно, параметрические уравнения
этой прямой:

Из полученных уравнений находим, что
точке
![]() соответствует значение параметра
соответствует значение параметра![]() ,
а точке
,
а точке![]() значение
значение![]() .
.
По определению дифференциала

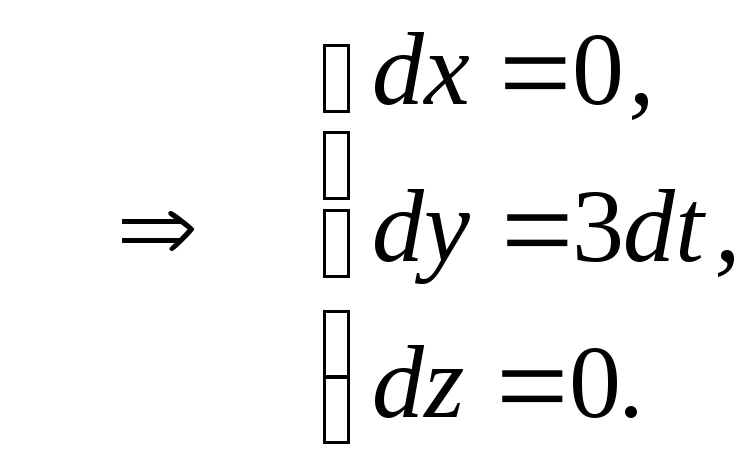
Учитывая, что
![]() и
и![]() ,
подставляем в интеграл только значения
,
подставляем в интеграл только значения![]() и
и![]() ,
а также значения параметра
,
а также значения параметра![]() и
и![]() ,
соответствующие началу и концу дуги
,
соответствующие началу и концу дуги![]()
![]()
![]() .
.
Пример. Вычислить![]() ,
где
,
где![]() —плоская
кривая, являющаяся частью параболы
—плоская
кривая, являющаяся частью параболы![]() от точки
от точки![]() до точки
до точки![]() .
.
Решение. Изобразим на рисунке линию
интегрирования![]() .
.

Воспользуемся формулой:
![]()
![]()
В данном случае
![]() соответствуют началу и окончанию пути
интегрирования,
соответствуют началу и окончанию пути
интегрирования,![]() ,
следовательно:
,
следовательно:
![]()
![]()
![]() .
.
