
- •Часть IV
- •Введение
- •Рабочая программа
- •Варианты контрольных заданий
- •Литература
- •Числовые ряды Числовой ряд. Общий член ряда
- •Сходящиеся и расходящиеся ряды
- •Основные свойства сходящихся рядов
- •Признаки сходимости числовых рядов
- •Знакочередующиеся и знакопеременные ряды Знакочередующиеся ряды
- •Знакопеременные ряды
- •Функциональные ряды Функциональный ряд и его область сходимости
- •Степенные ряды
- •Ряды тейлора и маклорена
- •Ряды фурье
- •1) Во всех точках непрерывности функции ;
- •2) Полусумме пределов функции слева и справа, т.Е., если является точкой разрыва первого рода, то .
- •Ряд Фурье в комплексной форме
- •Интеграл Фурье
- •220114 Г. Минск, Староборисовский тракт 8, к. 2.
Ряд Фурье в комплексной форме
Пусть
периодическая функция ![]() с периодом
с периодом ![]() разложена в ряд Фурье
разложена в ряд Фурье
![]() . (31)
. (31)
Из формулы Эйлера
![]() следует, что
следует, что
![]() и
и ![]() .
.
Тогда ![]() ;
;
![]() .
.
Подставив эти
выражения в (31) и отдельно группируя
слагаемые, содержащие ![]() и
и ![]() ,
получим
,
получим
![]() .
.
Если обозначить
![]() ;
;
![]() ;
;
![]() ,
то ряд примет вид
,
то ряд примет вид
![]() ,
,
а просуммировав
по отрицательным значениям ![]() ,
запишем комплексную форму ряда Фурье
в окончательном виде
,
запишем комплексную форму ряда Фурье
в окончательном виде
![]() . (32)
. (32)
Комплексные
коэффициенты Фурье ![]() вычисляются по формуле
вычисляются по формуле
![]()
![]() . (33)
. (33)
Для произвольного
периода ![]() формулы (31) и (32) принимают вид
формулы (31) и (32) принимают вид
![]() ;
; ![]()
![]() . (34)
. (34)
Модуль ![]() позволяет найти амплитуду
позволяет найти амплитуду ![]() -ой
гармоники
-ой
гармоники
![]() ;
; ![]() .
.
Комплексная форма ряда Фурье имеет более простой вид по сравнению с формулами (24, 25). Кроме того, в ряде случаев она облегчает вычисления.
В электротехнике
числа ![]() называют волновыми числами, а их
совокупность - спектром. Для ряда Фурье
спектр имеет дискретный характер.
называют волновыми числами, а их
совокупность - спектром. Для ряда Фурье
спектр имеет дискретный характер.
Пример 33. Разложить в ряд Фурье в комплексной форме периодическую функцию
![]()
Решение.
По формуле (33), интегрируя по частям,
находим коэффициент Фурье ![]() для
для ![]() .
.

Так как
![]() и
и ![]() ,
,
то ![]() .
.
Для ![]() имеем:
имеем:
![]() .
.
Используя формулу (31), получим ряд Фурье:
![]() .
.
Интеграл Фурье
Непериодическую
функцию можно представить как периодическую
с периодом ![]() .
При
.
При ![]() числа
числа ![]() будут охватывать все значения, то есть
спектр волновых чисел будет непрерывным,
и суммирование в ряде Фурье (34) заменится
на интегрирование.
будут охватывать все значения, то есть
спектр волновых чисел будет непрерывным,
и суммирование в ряде Фурье (34) заменится
на интегрирование.
Если непериодическая
функция f(t)
удовлетворяет условиям Дирихле на любом
конечном интервале и
![]() сходится, то ее можно представить
интегралом Фурье, который в комплексной
форме имеет вид
сходится, то ее можно представить
интегралом Фурье, который в комплексной
форме имеет вид
![]() (35)
(35)
где S(![]()
![]() . (36)
. (36)
![]() является аналогом коэффициента
является аналогом коэффициента ![]() (формулы 34 и 36). Однако, если
(формулы 34 и 36). Однако, если ![]() характеризует амплитуду волнового
числа
характеризует амплитуду волнового
числа ![]() ,
то
,
то ![]() - плотность распределения комплексной
амплитуды. Поэтому данную функцию
называют спектральной
плотностью или
спектральной
функцией. Ее
модуль
- плотность распределения комплексной
амплитуды. Поэтому данную функцию
называют спектральной
плотностью или
спектральной
функцией. Ее
модуль ![]() называют амплитудой спектральной
плотности или амплитудным спектром.
называют амплитудой спектральной
плотности или амплитудным спектром.
Формулу (36) называют прямым преобразованием Фурье, а формулу (35) - обратным. Вместе они составляют пару преобразований Фурье.
В точках разрыва функции интеграл Фурье как и сумма ряда Фурье равен полусумме пределов функции слева и справа.
Интеграл Фурье можно представить аналогично формулам (24-25), то есть без комплексных выражений
![]() ,
,
где ![]() ,
,
![]() .
.
Спектральная
плотность ![]() выражается через функции
выражается через функции ![]() и
и ![]() следующим образом
следующим образом
![]() . (38)
. (38)
Пример 34. Найти спектр прямоугольного импульса.
Прямоугольный
импульс (рис.5) высотой ![]() и длительностью
задан уравнениями:
и длительностью
задан уравнениями:
![]()
![]() =
=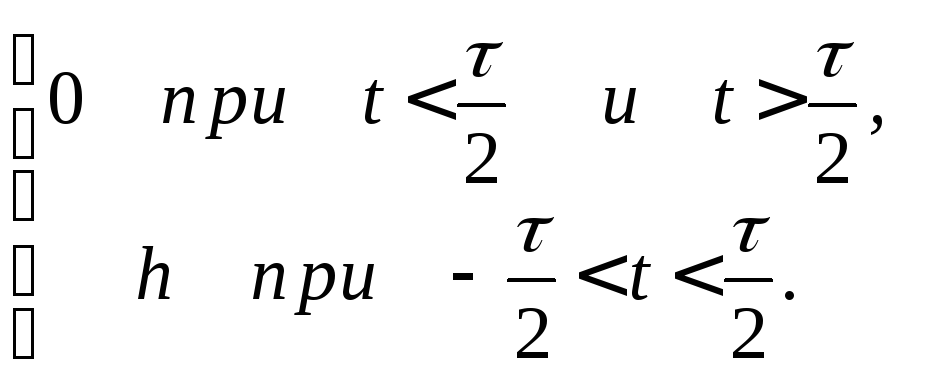

По формуле:
![]() ,
находим спектральную плотность.
,
находим спектральную плотность.

![]()

Так как ![]() -
площадь импульса, то
-
площадь импульса, то 
ВОПРОСЫ И УПРАЖНЕНИЯ ДЛЯ САМОПРОВЕРКИ
1. Что называется числовым рядом, частичной суммой, общим членом ряда, его суммой?
2. Запишите ряд в кратком виде. После записи проверьте, получаются ли из них все члены ряда:
а) ![]() ;
;
б) ![]() .
.
3. Сформулируйте необходимый признак сходимости ряда . Используя его, докажите расходимость рядов:
а) ![]() ; б)
; б)
![]() ; в)
; в)
![]() .
.
4. Сформулируйте достаточные признаки сходимости рядов с положительными членами: признак Даламбера, признаки Коши. Исследуйте на сходимость ряды:
а)![]() . Ответ:
ряд сходится .
. Ответ:
ряд сходится .
б) ![]() . Ответ:
ряд расходится .
. Ответ:
ряд расходится .
в) ![]() . Ответ:
ряд расходится .
. Ответ:
ряд расходится .
5. Сформулируйте признак Лейбница сходимости знакочередующихся рядов.
6. Дайте определение абсолютно и условно сходящихся рядов.
7. Что называется областью сходимости функционального ряда?
8. Выведите формулу для вычисления радиуса сходимости степенного ряда?
9. Как исследуется сходимость степенного ряда в граничных точках области сходимости?
10. Найти области сходимости следующих рядов:
а) ![]() Ответ.
Ответ.
![]() при x
=-2
при x
=-2
ряд сходится условно.
б) ![]() Ответ.
Ответ.
![]()
в) ![]() Ответ.
Ответ.
![]()
11.Разложить в ряд по степеням x следующие функции:
а) ![]() Ответ.
Ответ.![]()
![]()
б) ![]() Ответ.
Ответ.![]()
![]()
в) ![]() Ответ.
Ответ.![]()
![]()
Указание.
Использовать формулу ![]()
12. Вычислить
приближенно ![]() ,
воспользовавшись рядом
,
воспользовавшись рядом
![]()
и взяв сумму первых пяти членов при х=1. Какова будет величина допущенной ошибки?
Разложить функцию в ряд Фурье
а) ![]()
б) 
Ответ:
а) ![]() б)
б)
![]() .
.
14. Разложить функцию в ряд Фурье по косинусам, продолжив ее в симметричный интервал:
а) ![]() Ответ:.
Ответ:.
![]() .
.
б) ![]() Ответ:
Ответ:
![]() .
.
Написать формулу прямого и обратного преобразований Фурье.
Что называется спектральной плотностью?
Найти комплексный и амплитудный спектр функции
![]() Ответ:
Ответ:
![]() ,
,
![]() .
.
КОНТРОЛЬНАЯ РАБОТА № 4.
Исследовать знакоположительные числовые ряды (а) на сходимость и знакочередующиеся числовые ряды (б) на абсолютную и условную сходимость.
1. а) ![]() ; б)
; б)
![]() .
.
2. а) ![]() . б)
. б)
![]()
3. а) ![]() ; б)
; б)
![]() .
.
4. а) ![]() ; б)
; б)
![]() .
.
5. а) ![]() ; б)
; б)
![]() .
.
6. а) ![]() ; б)
; б)
![]() .
.
7. а) ![]() ; б)
; б)
![]() .
.
8. а) ![]() ; б)
; б)
![]() .
.
9. а) ![]() б)
б)
![]() .
.
10 а) ![]() ; б)
; б)
![]()
Найти интервал сходимости степенного ряда и выяснить вопрос о сходимости ряда на концах интервала.
Таблица 1.
-
11

16

12

17
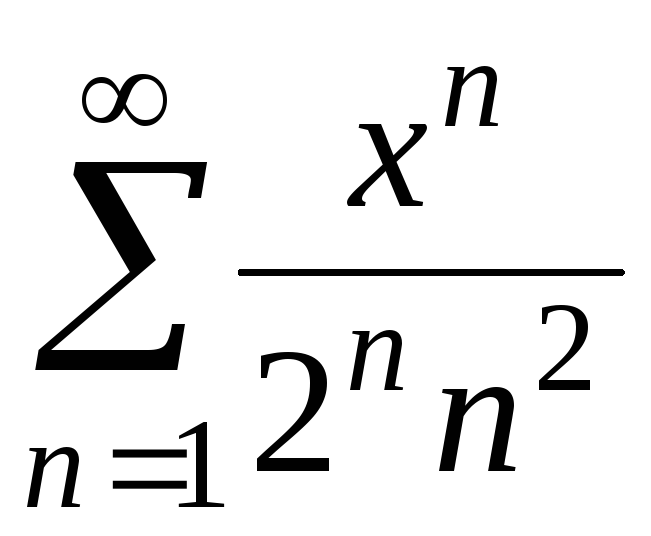
13

18
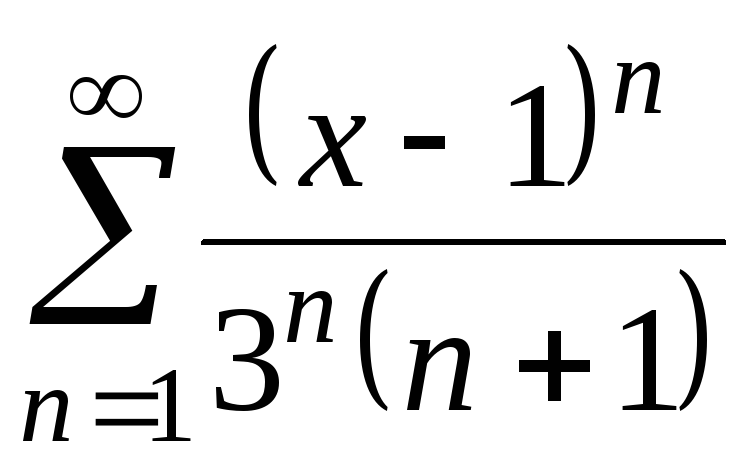
14

19

15

20

Разлагая
подынтегральную функцию в ряд, вычислить
приближенно значение определенного
интеграла ![]() с точностью до =0,001.
с точностью до =0,001.
![]()
![]() Таблица 2.
Таблица 2.
|
№ |
|
b |
№ |
|
b |
|
21 |
|
1 |
26 |
|
|
|
22 |
|
|
27 |
|
2 |
|
23 |
|
1 |
28 |
|
|
|
24 |
|
1 |
29 |
|
1 |
|
25 |
|
1 |
30 |
|
|
Разложите в ряд Фурье периодическую функцию, аналитическое выражение которой задано на промежутке длиной, равной периоду.
31. 
![]() 32.
32. 
![]()
33. 
![]() 34.
34. 
![]()
35. 
![]() 36.
36. 
![]()
37. 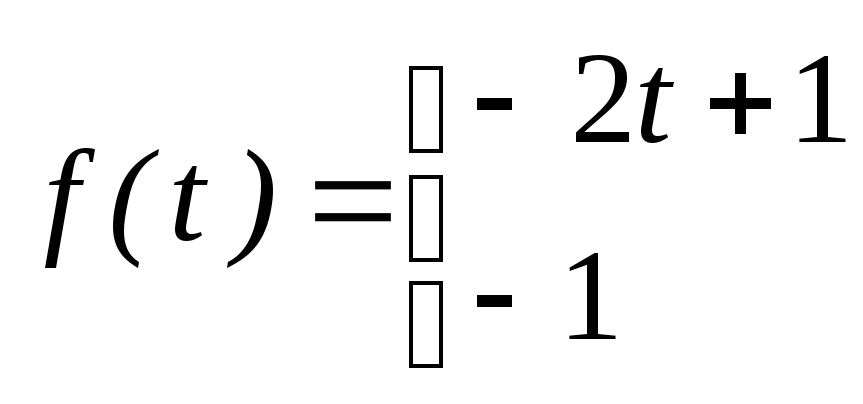
![]() 38.
38. ![]() ,
,
![]()

 Т=1. 40.
Т=1. 40.  ,
,



Разложите функцию
![]() в
ряд Фурье по синусам. Постройте график
суммы ряда.
в
ряд Фурье по синусам. Постройте график
суммы ряда.
41. 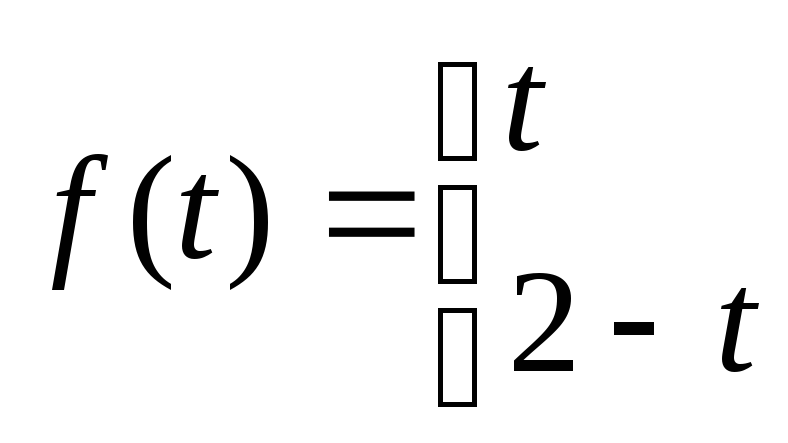
![]() 42.
42. ![]()
![]()
43. ![]()
![]() 44.
44. 

45. ![]()
![]() 46.
46. 
![]()
47. 
 48.
48. ![]()
![]()
49. ![]()
![]() 50.
50. ![]()
![]()
Найдите преобразование
Фурье функции ![]() .
.
51. 
![]() 52.
52.



 54.
54.
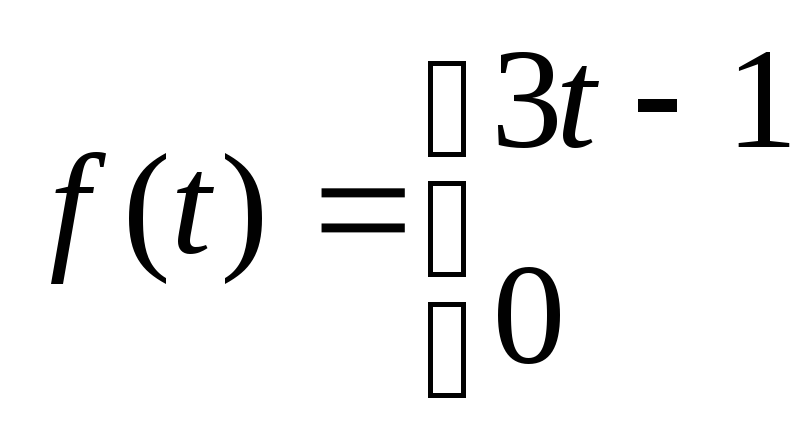


 56.
56.


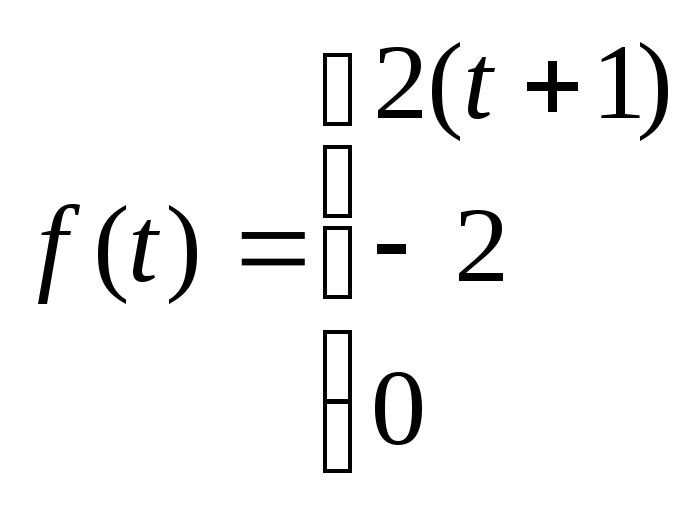
 58.
58.
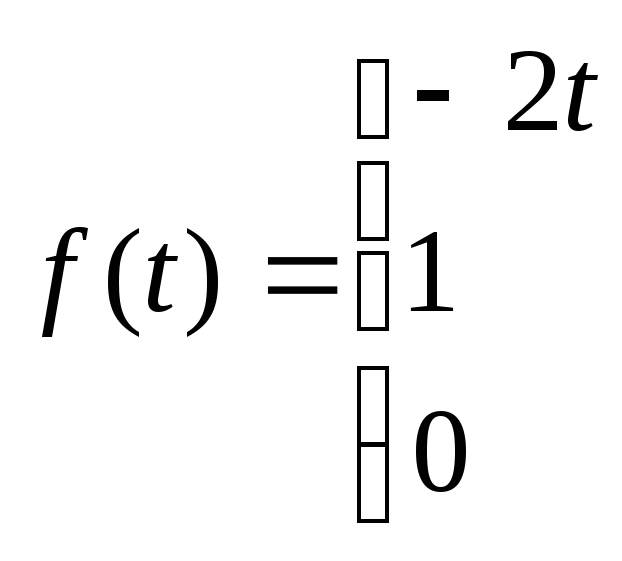


 60.
60.


С О Д Е Р Ж А Н И Е
|
Введение Рабочая программа Варианты контрольных заданий Литература Числовые ряды Числовой ряд. Общий член ряда Сходящиеся и расходящиеся ряды Основные свойства сходящихся рядов Признаки сходимости числовых рядов Необходимый признак сходимости ряда Достаточные признаки сходимости знакоположительных рядов Знакочередующиеся и знакопеременные ряды Знакочередующиеся ряды Знакопеременные ряды Функциональные ряды Функциональный ряд и его область сходимости Степенные ряды Ряды Маклорена и Тейлора Ряды Фурье Ряд Фурье в комплексной форме Интеграл Фурье Вопросы и упражнения для самопроверки Контрольная работа №4 |
3 3 4 5 6 6 6 7 8 8 9 14 14 15 18 18 19 21 24 30 32 33 36 |
План 2001/2002, поз. 31
Гладков Лев Львович
Гладкова Галина Александровна
Методические указания и контрольные задания по дисциплине «Высшая математика», часть IV для студентов уровня ВО заочной формы обучения специальности 145. 01. 03 «Сети телекоммуникаций»
Редактор Вердыш Н.В.
Подписано к печати 20.12.2002
Формат 60S84/16
Усл. Печ. Л. 2,3. Уч. - изд. Л. 2,0
Тираж 90 экз. Заказ 675.
Высший государственный колледж связи
