Дифференцируемость функции

Определение. Если для функции в точке существует предел

, (1)

то говорят, что при данном значении функция дифференцируема

или (что равносильно этому) имеет производную.

Если функция дифференцируема в каждой точке некоторого отрезка ( или интервала ), то гово­рят, что она дифференцируема на отрезке ( или на интервале ).

Связь между непрерывностью и дифференцируемостью функции в данной точке устанавливает

Теорема. Если функция дифференцируема в некото­рой точке, то она и непрерывна в этой точке.

Доказательство. Действительно, если функция дифференцируема в точ­ке , то существует предел

,

Следовательно,

,

где ― бесконечно малая функция при .

Умножим последнее равенство на

(2)

Тогда

что и означает ( по определению 3 ) непрерывность функции в точке .

⊠

Утверждение, обратное данной теореме, вообще говоря, неверно, т. е. из непрерывности функции в точке еще не следует ее дифференцируемость в этой точке.

Например, рассмотрим функцию . Очевидно, что эта функция определена и непрерыв­на на . Но в точке не имеет производной, т.к. не существует — не равны левосторонний и правосторонний пределы:

,

Замечание. Так как равенство (1) равносильно равенству (2), то часто функцию называют дифференцируемой в точке , если ее приращение может быть представлено в виде (2).

Дифференциал функции

Пусть функция дифференцируема в точке , т.е. ее прира­щение в этой точке предста­вимо в виде

,

где ― бесконечно малая функция при .

Отсюда если , то

.

Следовательно, при приращение функции и выраже­ние являются эквивалентными бесконечно малыми функци­ями, т. е. при можно приближенно считать, что ∼.

Определение. Величину , являющуюся главным (линейным) членом приращения функции в точке , называют дифференциа­лом функции и обозначают (или ).

Таким образом, по определению

=.

Найдем дифференциал функции , В этом случае и, следовательно, , т. е. дифференциал и приращение независимой переменной равны между собой. Поэтому дифференциал функции в точке можно представить в виде

=.

Следовательно, производную функции можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной:

или в более краткой записи .

На рисунке, представленном ниже, дана геометрическая интерпретация дифференциала функции . Так как , то дифференциал функции изме­ряется отрезком , т. е. диффе­ренциал функции в точ­ке изображается приращением ординаты точки касательной, про­веденной в к линии .

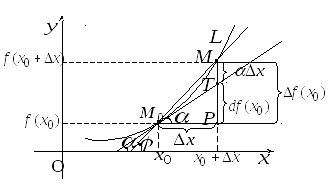
Дифференциал функции можно использовать для вычисления приближенных значений функции. Действительно, заменяя прира­щение функции в точке ее дифференциалом, получаем формулу для прибли­женных вычислений:

.

Пример. Вычислить приближенно .

Решение. Принимая , , , следовательно, , , .

Тогда : .