Точки локального экстремума функции. Необходимое и достаточные условия существования экстремума функции

Экстремум функции. Особую роль в исследовании поведения функции на множестве играют точки, разделяющие интервалы воз­растания и убывания функции

Определение. Точка называется точкой локального макси­мума (минимума) функции , если существует проколотая -окрестность точки , такая, что для всех выполняется неравенство <0 (>0) Значение называют локальным максимумом (минимумом) функ­ции и пишут

().

Точки максимума или минимума функции называют точками экстремума функции, а максимумы и минимумы функции называ­ются экстремумами функции.

Из приведенных рассуждений следует, что экстремумы функции носят локальный характер — это наибольшее или наименьшее зна­чения функции по сравнению с близлежащими ее значениями.

Если функция на имеет несколько максимумов и минимумов, то возможен случай, когда максимум функции меньше ее минимума.

Например, на рисунке точки , являются точками максимума функции , а , — точками ее минимума, но <.

Наименьшее и наибольшее значения функции на в отличие от локальных ее экстремумов называют абсолютными минимумом и максимумом функции и обозначают ,

Необходимое условие существования экстремума функции

Теорема . Если в точке функция достигает экстремума, то ее производная в этой точке равна нулю или не существует.

Доказательство. Пусть в точке достигает максимума. Тогда существует , такая, что >

>, при .

При >0,

При <0.

Если пределы левых частей этих неравенств при сущест­вуют, то это будут соответственно производные функции справа и слева:

0,

0.

Если производные функции в точке , то существует .

Если и отличны от нуля, то не сущест­вует.

Аналогично доказывается случай, когда — точка минимума.

⊠

Геометрический смысл этой теоремы заключается в следующем: в точках экстремума функции касательная к ее графику парал­лельна оси абсцисс, если в этих точках существует производная.

Точки, в которых производная функции обращается в нуль или не существует, называют критическими или точками воз­можного экстремума. Точки, в которых производная функции обращается в нуль, называют стационарными.

Не всякая критическая точка функции является точкой ее локального экстремума. Например, производная функции в точке обращается в ноль, но не является точкой локального экстремума функции. В этой точке функция возрастает.

Достаточные условия существования экстремума

Теорема. (первый достаточный признак существования экст­ремума функции). Пусть — критическая точка непрерывной функ­ции . Если при переходе через точку меняет знак с « + » на « — », то — точка локального максимума; если при переходе через точку меняет знак с « — » на « + », то — точка локального минимума; если при переходе через точку не меняет знак, то не является точкой локального экстремума.

Доказательство. Пусть — точка возможного экстремума, причем >0 и <0 .

Тогда по теореме о достаточном признаке возрастания и убывания функции функция возрастает при ( т.е. > ) и убывает при ( т.е. < ),

т. е. точка является точкой локального максимума.

Аналогично доказывается и существование точки локального

минимума.

Если сохраняет знак в окрестности точки , то в этой окрест­ности функция монотонна, т. е. точка не является точкой локаль­ного экстремума.

⊠

На рисунке дана геометрическая интерпретация точки локаль­ного максимума.

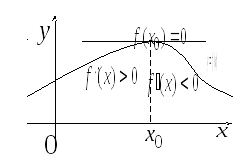
Теорема (второй достаточный признак существования экст­ремума функции). Стационарная точка функции , дважды дифференцируемой в , является точкой локального минимума , если > 0, и точкой локального максимума, если < 0.

Доказательство. Пусть выполнены условия теоремы и > 0. Тогда в возрастает, но = 0, следовательно, в при переходе через точку меняет знак с « — » на « + » . Согласно первому достаточному признаку существования экстремума функции, точка является точкой локального минимума функции .

Если <0, то в '(х) убывает, но = 0, следова­тельно, в при переходе через точку производная функции меняет знак с « + » на « — » Тогда, согласно первому достаточному признаку существования экстремума функции, точка является точкой локального максимума функции .

⊠