Поверхности (линии) уровня

Пусть в трехмерном пространстве имеется область D, в которой задана функция

.

В этом случае говорят, что в области Dзадано скалярное поле.

Если, например, функция обозначает температуру в точке, то говорят, что задано скалярное поле температур; если областьDзаполнена жидкостью или газом иобозначает давление, то имеется скалярное поле давлений и т. д.

Рассмотрим точки области D, в которых функцияимеет постоянное значение:

.

Совокупность этих точек образует некоторую поверхность. Если возьмем другое значение , то получим другую поверхность. Эти поверхности называются поверхностями уровня.

Пример. Пусть задано скалярное поле

.

Здесь поверхностями уровня будут поверхности

,

т. е. эллипсоиды с полуосями ,,.

Если функция есть функция двух переменныхи:

,

то «поверхностями» уровня будут линии на плоскости :

,

которые называются линиями уровня.

Если значения мы будем откладывать по оси, то линиями уровня на плоскостибудут проекции линий, которые получаются в пересечении поверхностис плоскостями. Зная линии уровня, легко исследовать характер поверхности.

Пример. Определить линии уровня функции.

Решение.Линиями уровня будут линии с уравнениями. Это окружности радиуса. В частности, приполучаем окружность. График данной функции, а также получаемые линии уровня изображены на рисунке.

Предел функции нескольких переменных

Приведем определение предела функции двух переменных по Коши.

Определение.Число А называется пределом функциипри, т.е. в точке, если для любогосуществует, такое, что при всех, удовлетворяющих условиями, выполняется неравенство— А.

Данное определение в символьном виде можно записать так:

Для обозначения предела функции в точкеиспользуют и другую форму записи:

.

Замечание. При определении предела функциив точкеполагают, что функция может быть и не определена в самой точке.

Пример.Доказать, пользуясь определением предела по Коши, что .

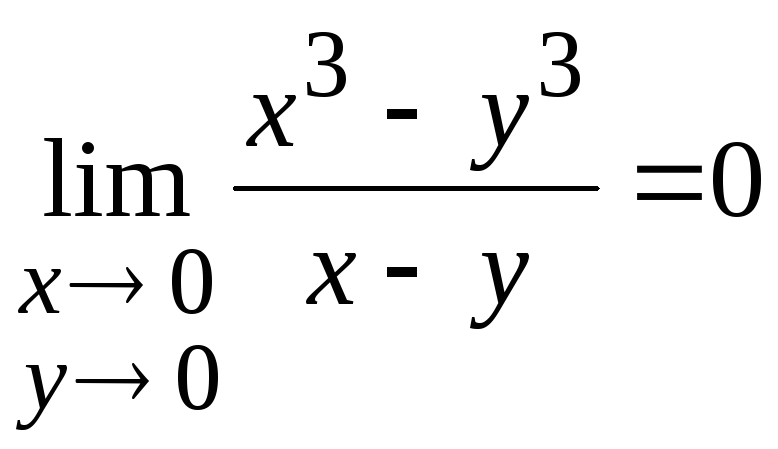Решение.Область определения данной функцииD. Выберем произвольное числои найдем, такое, что для любой точки, для которой справедливо,выполняется неравенство. Так как для любой точкиDсправедливо соотношение

,

то

.

Оценим :

.

Таким образом,

,

где — расстояние от точкидо точки.

Следовательно, для любого мы нашли число, такое, что для любой точки, принадлежащей-окрестности точки, т.е. при,будет выполняться неравенство

.

Что и требовалось доказать.

Приведенные выше определения предела функции двух переменных без труда обобщаются на случай функций трех и более переменных. Обобщим, например, определение предела по Коши на случай функции независимых переменных.

Определение.Число А называется пределом функциипри,т.е. в точке, если для любогосуществует, такое, что при всех , удовлетворяющих условиям,,…,, выполняется неравенство— А.

Пользуясь понятием предела функции, можно дать определение бесконечно малой функции при (), вывести основные свойства бесконечно малых функций, сравнить бесконечно малые функции, доказать теорему о том, что разность между функцией, имеющей предел, и ее пределом есть бесконечно малая функция, сформулировать основные теоремы об арифметических операциях над пределами. Все эти теоремы для случаябыли рассмотрены при изучении функций одной переменной.