Тройной интеграл

По аналогии с двойным интегралом вводится понятие тройного интеграла. Рассмотрим ограниченную замкнутую пространственную область и определенную в ней непрерывную функцию. Областьразобьем наэлементарных пространственных областей. Предполагается, что областьи элементарные областиимеют объемы, которые будем обозначать соответственно теми же символами. В каждой элементарной области() выберем произвольную точку, значение функции в этой точкеумножим на объем элементарной областии составим сумму всех таких произведений:

,

которая называется интегральной суммой данной функции по данному объему.

Обозначим через диаметр области. Пусть— наибольший из этих диаметров. И перейдем в последнем равенстве к пределу при.

Если предел интегральной суммы существует, то он и называется тройным интегралом от функции по пространственной области.

Итак, по определению

. (1)

Тройной интеграл от функции по пространственной областитакже обозначается следующим образом:

.

Отметим без доказательства, что если функция непрерывна в рассматриваемой замкнутой области, то предел в правой части формулы (1) существует и не зависит от способа разбиения областина элементарные и выбора точкив элементарной области.

Предположим, что в области распределено вещество, объемная плотность которого задана непрерывной функцией, тогда произведениевыражает приближенную массу элементарной области, интегральная сумма — приближенную массу всей области, а тройной интеграл — точное значение этой массы, т. е.

.

Данная формула выражает механический смысл тройного интеграла: тройной интеграл представляет массу, заполняющую область интегрирования .

Если в формуле , томы получаем формулу для вычисления объема с помощью тройного интеграла:

или

Тройной интеграл обладает свойствами, аналогичны­ми свойствам двойного интеграла.

Перейдем к вопросу о вычислении тройного интеграла в прямоугольных декартовых координатах. Предположим, что область является стандартной в направлении оси, т. е. удовлетворяющей следующим условиям:

1) всякая прямая, параллельная этой оси и имеющая с данной областью общие точки, пересекает границу области только в двух точках;

2) проекция областина плоскостьпредставляет собой стандартную область в направлении осиили оси.

Пусть стандартная область ограничена сверху поверхностью, снизу — поверхностью, тогда можно показать, что

.

Если область является стандартной в направлении осии определяется неравенствами,, то

.

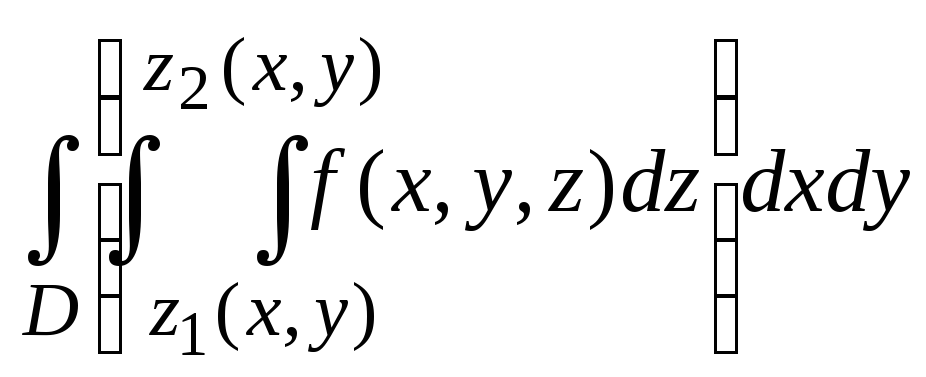
Следовательно, в этом случае

.

Замечание.Если областьявляется стандартной в направлении осии определяется неравенствами,, то

.

Замечание.Если областьявляется стандартной в направлении каждой координатной оси и ее проекции на координатные плоскости являются стандартными в направлении каждой соответствующей оси, то пределы интегрирования в трехкратном интеграле можно расставить шестью различными способами.

Пример. Вычислить тройной интегралпо области, ограниченной поверхностями,,,,,.

Решение. Изобразим область.

Эта область является стандартной в направлении оси , а проекцияобластина плоскостьпредставляет собой стандартную область в направлении оси. Следовательно,

.

Пример. Найти объем тела, ограниченного поверхностями,.

Решение.Уравнения поверхностей, ограничивающих тело имеют наиболее простой вид в цилиндрических координатах, связь которых с декартовыми осуществляется по формулам:

,,.

Первая поверхность являющаяся параболоидом вращения примет вид:

.

Уравнение плоскости в цилиндрических координатах останется без изменений.

Изобразим тело, объем которого необходимо найти, на рисунке.

Решая совместно уравнения и, получаем, что областьпроектируется в плоскостьв круг.

Следовательно,

.