11. Передаточные ачх и фчх последовательного колебательного контура, его избирательные свойства. Полоса пропускания. Прохождение через колебательный контур сигналов негармонической формы

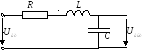
Обычно спектр частот радиосигнала составляет 2-3% от несущей частоты, поэтому можно приблизительно считать

— передаточная АЧХ последовательного контура в абсолютных координатах

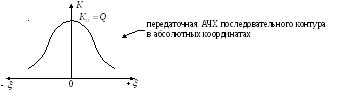
Вывод:на резонансной частоте коэффициент передачи последовательного контура максимальный:.

ФЧХ:

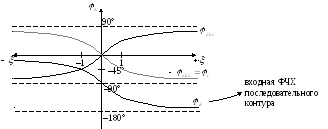
На выходе стоит конденсатор, поэтому напряжение выхода отстаёт от тока на 90°. Угол практически равен углу выходного напряжения, поэтому характеристикусдвигаем на 90° вниз:

Передаточная ФЧХ имеет линейный участок при расстройках от до.

Прохождение через колебательный контур сигналов негармонической формы. Избирательные свойства последовательного контура

Избирательность— способность цепи различать сигналы по частоте. Подадим на последовательный контур сигнал, который состоит из 5 гармоник одинаковой амплитуды.

На выходе амплитуда сигнала не резонансной частоте будет максимальной, т. к. , и на этой частоте самый большой коэффициент передачи.

Вывод:последовательный контур обладает избирательностью по напряжению. Он выделяет сигнал резонансной частоты.

Полоса пропускания контура— область частот, на границах которой модуль комплексного коэффициента передач уменьшается враз по сравнению с резонансным.

На уровне полосы пропускания коэффициент обозначается :

Нарисуем передаточную характеристику :

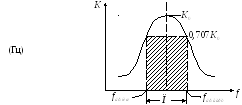
Вывод:чем выше добротность, тем уже полоса пропускания контура.

1)

2)

Кривые тока и напряжения такого вида называются резонансными.

Примечание:

При малых расстройках напряжение на катушке и конденсаторе можно рассчитать по формуле:

12. Принципиальная схема параллельного колебательного контура. Резонанс токов в параллельном колебательном контуре, условие резонанса. Свойства электрической цепи при резонансе токов. Резонансная частота, добротность

Контур называется параллельным, если катушка, конденсатор и источник соединены параллельно.

В параллельном контуре может возникнуть резонанс токов, когда напряжение и ток на входе совпадают по фазе:.

— условие резонанса токов

Проводимость индуктивная равна проводимости емкостной.

При резонансе токов сопротивление параллельного контура максимально.

Свойства цепи при резонансе токов:

1. Ток в момент резонанса:

При резонансе токов общий ток минимальный.

2. На практике ,

При резонансе токов токи ветвей приблизительно равны.

3. Построим векторную диаграмму для резонанса токов:

Если бы (контур идеальный), то токи, и общий ток был бы равен 0, но т. к. есть небольшое, то существует активная составляющая тока (маленькая) и общий ток равен этой активной составляющей.

4. Выведем формулу резонансной частоты. Для этого

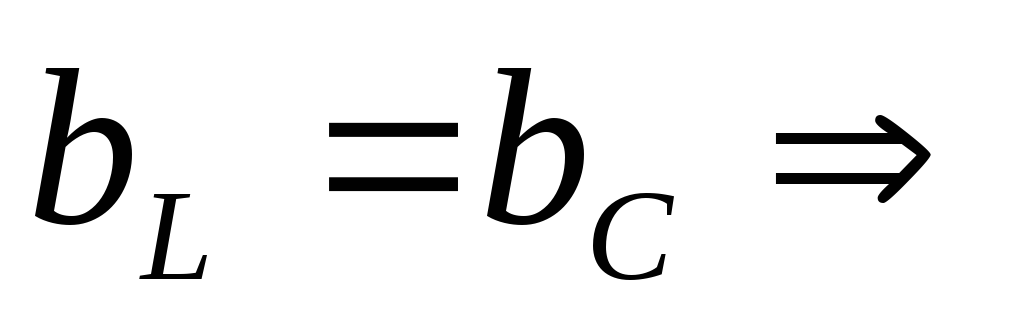
Вывод:резонанс токов наступает тогда, когда частота питающего напряжения равна частоте собственных колебаний контура.

Получить резонанс токовможно, изменяяLилиC, или частоту питающего напряжения.

5. Энергетический процесс при резонансе токов такой же, как и при резонансе напряжений:

Рассчитаем токи в момент резонанса:

Вывод:добротность в параллельном контуре показывает, во сколько раз токи ветвей больше общего тока в момент резонанса, поэтому это явление и называется резонанс тока.