Многопороговое декодирование сск

Сверточные коды способны корректировать не только случайные ошибки кратностью , но и пакеты ошибок кратностьюt_n=k₀. Для их коррекции предложен алгоритм многопорогового или многоступенчатого декодирования.

Сущность многопорогового декодирования ССК состоит в том, что после первого декодера ССК включается второй пороговый декодер ССК, далее третий декодер и т.д. Однако для практических применений, как показывают расчеты, вполне достаточно трех пороговых декодеров (ступеней декодирования), которые обеспечивают повышенную достоверность передачи данных. Обобщенная структурная схема двухпорогового декодера ССК сR=1/2 представлена на рис. 8.

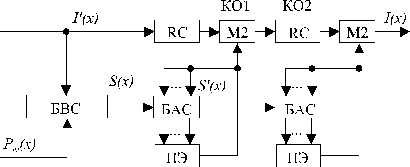
Рис. 8 Обобщенная структурная схема двухпорогового декодера ССК с R=1/2

БВС – блок вычисления синдрома; КО – корректор ошибок; БАС – блок анализа синдрома; ПЭ – пороговый элемент

Особенность многопорогового алгоритма декодирования ССК состоит в оптимальном выборе количества ступеней декодирования и величины порогов в каждой ступени декодирования. Показано, что многопороговый алгоритм декодирования применим для ССК с R1/2 и J3. При J=3 и J=4 (R1/2) в многопороговом декодере возможна реализация только двух ступеней декодирования, а при J5 – реализация трех и более ступеней декодирования. Это определяется тем, что первая ступень декодирования корректирует “случайным образом”, как правило, одиночные ошибки, а последующие ступени декодирования в зависимости от значений R и J могут быть настроены на коррекцию как одиночных, так и многократных ошибок. Корректирующая способность каждой ступени декодирования определяется выбранным значением порога декодирования. Так, например, для ССК с R=1/2 и J=3 величина порога в первой ступени декодирования двухпорогового декодера, приведенного на рис. 8, выбирается равной П₁=J=3, а во второй ступени декодирования П₂=J – 1=3 – 1=2. При J=4 порог в первой ступени декодирования выбирается равным П₁=J=4, а во второй ступени ; при J5 пороги в первой и второй ступенях декодирования выбираются соответственно равными П₁=J=5, П₂=J – 1=5 –1=4, а в третьей ступени декодирования.

Таким образом, коррекция ошибок каждой ступенью декодирования обеспечивает более высокую достоверность исправления ошибок после­дующими ступенями декодирования. Следовательно, при оптимально выбранном ко­ли­чест­ве ступеней декодирования можно обеспечить высокую достовер­ность и ско­рость обработки информации при невысоких затратах на реализа­цию декодера.

Анализ многопорогового декодирования показывает, что энерге­ти­ческий выигрыш увеличивается на 0,21 дБ при последовательном увеличении количества ступеней декодирования при R=const и J=const. При R=const и увеличении количества проверок (J+1) энергетический выигрыш увели­чи­ва­ется на 0,3 … 0,4 дБ.

Структурная схема декодера

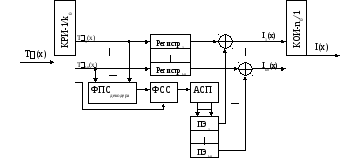
КРИ-1/k₀– коммутатор распределения информации;

ФПС_{декодера}– формирователь проверочных символов декодера;

ФСС – формирователь символов синдрома;

АСП – анализатор синдромной последовательности;

ПЭ – пороговый элемент;

КОИ-n₀/1 – коммутатор объединения информации.