- •«Теория кодирования»
- •Первичные коды и эффективное кодирование
- •Префиксные коды
- •Примерами префиксных кодов являются коды Шеннона-Фано и Хаффмана. Код Шеннона-Фано
- •Код Хаффмана
- •Кодирование факсимильных изображений. Коды кдс-1, кдс-2, кдс-3
- •Основные параметры помехоустойчивых кодов
- •Классификация помехоустойчивых кодов
- •Коды: общие сведения, основные свойства
- •Линейные блоковые коды
- •Условия и свойства формирования разрешенных кодовых последовательностей лбк
- •Задание линейных кодов с помощью порождающих и проверочных матриц
- •Кодирование информации линейным блоковым кодом
- •Синдромное декодирование
- •Мажоритарное декодирование
- •Циклические коды: общие сведения, определение
- •Свойства циклических кодов
- •Способ построения кодовых последовательностей с использованием порождающей матрицы
- •Назначение и способы построения проверочной матрицы циклического кода
- •Способ формирования кодовых последовательностей циклического кода с использованием образующего полинома
- •Многотактные фильтры
- •Кодирование информации циклическими кодами
- •Декодирование информации циклическими кодами
- •Синдромный метод декодирования цк
- •I Табличное синдромное декодирование
- •II Схемное синдромное декодирование
- •Многомерные коды: определение, классификация
- •Матричные коды: определение, принцип построения, свойства, параметры, достоинства и недостатки
- •Итеративные коды: определение, принцип построения, основные характеристики
- •Каскадные коды: определение, принцип построения, основные характеристики
- •Сверточные коды: определение, параметры, классификация
- •Задание систематических сверточных кодов
- •I. Задание систематических ск с помощью порождающей матрицы g(х)
- •II. Задание систематических ск с помощью проверочной матрицы h(х)
- •III. Задание систематических ск с помощью разностных треугольников
- •Кодирование информации сверточными кодами
- •Структурная схема кодера
- •Жесткое пороговое декодирование сск
- •Мягкое пороговое декодирование сск
- •Многопороговое декодирование сск
- •Структурная схема декодера
- •Список литературы
Кодирование информации циклическими кодами
Кодирование неразделимымциклическим кодом заключается в умножении полинома сообщения на генераторный полиномF(x)=Q(x)*P(x).
Рассмотрим кодирование неразделимым ЦК на примере: P(x)=1+x3+x4, Q(x)=1+x2+x3.
F(x)=Q(x)*P(x)=(1+x2+x4)(1+x3+x4)=1+x2+x4+x5+x7=10101101
Для реализации кодера потребуется два сумматора по модулю два и 4 триггерных ячейки (элемента задержки), т.к. 4 – это максимальная степень полинома P(x).
Кодирование будет проходить за (n+m)+1=4+3+1=8 тактов, где m и n – это максимальные степени полиномов Q(x) и P(x).
Схема кодера с вынесенными сумматорами приведена на рисунке. На вход схемы поступает многочлен Q(x), начиная с коэффициентов высших порядков.
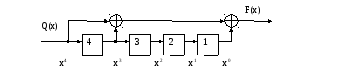
Таблица пошаговой работы схемы
|
шаг |
Q(x) |
4 |
3 |
2 |
1 |
F(x) |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
1 |
|
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
3 |
0 |
0 |
1 |
1 |
0 |
1 |
|
4 |
1 |
1 |
0 |
1 |
1 |
1 |
|
5 |
0 |
0 |
1 |
0 |
1 |
0 |
|
6 |
0 |
0 |
0 |
1 |
0 |
1 |
|
7 |
0 |
0 |
0 |
0 |
1 |
0 |
|
8 |
0 |
0 |
0 |
0 |
0 |
1 |
– начальное состояние
F(x)i=Q(x)i4i-11i-1
При кодировании разделимым кодомсуществует два варианта построения
кодирующего устройства в зависимости
от соотношения между![]() иl:
иl:
1) если k> l,
то кодер реализуется по порождающему
полиному![]() ;
;
2) если k< l,
то кодер реализуется по проверочному
полиному![]() .
.
При этом минимизируется число ячеек памяти в регистре сдвига.
Кодер, реализованный по полиному g(x)содержит![]() -разрядный
регистр сдвига и определяет остаток от
деленияQ(x)xlна генераторный полиномP(x).
-разрядный
регистр сдвига и определяет остаток от
деленияQ(x)xlна генераторный полиномP(x).
Пример: P(x)=1+x2+x3, Q(x)=1+х+x2+x3.
Схема кодера изображена на рисунке и
работает следующим образом: вначале
ключ
![]() находится в положении 1, а ключ
находится в положении 1, а ключ![]() замкнут. Информационные символы,
подаваемые на вход через ключ
замкнут. Информационные символы,
подаваемые на вход через ключ![]() ,
поступают на выход, а через ключ
,
поступают на выход, а через ключ![]() – в кодирующее устройство, где через
– в кодирующее устройство, где через![]() =4
тактов образуется
=4
тактов образуется![]() =7-4=3
проверочных символа. После этого ключ
=7-4=3
проверочных символа. После этого ключ![]() переводится в положение 2, а ключ
переводится в положение 2, а ключ![]() –
размыкается. Затем регистр делает еще
–
размыкается. Затем регистр делает еще![]() =3
такта, выдавая контрольные символы из
ячеек регистра на выход кодера.
=3
такта, выдавая контрольные символы из
ячеек регистра на выход кодера.

Таблица пошаговой работы схемы
|
шаг |
Q(x) |
z |
1 |
2 |
3 |
F(x) |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
2 |
1 |
0 |
0 |
1 |
0 |
1 |
|
3 |
1 |
1 |
1 |
0 |
0 |
1 |
|
4 |
1 |
1 |
1 |
1 |
1 |
1 |
|
5 |
0 |
0 |
0 |
1 |
1 |
1 |
|
6 |
0 |
0 |
0 |
0 |
1 |
1 |
|
7 |
0 |
0 |
0 |
0 |
0 |
1 |
– начальное состояние
zi=Q(x)i3i-1
1→2 (2i=1i-1)
3i=2i-1zi
F(x)i=Q(x)i
Перед 5-ым тактом переключаются ключи в схеме
Получили F(x)=1111111
Кодер, реализованный по полиному h(x),работает следующим образом: сначала
ключ![]() находится в положении 1, и на вход подаются
информационные символы. После
находится в положении 1, и на вход подаются
информационные символы. После![]() тактов информационные символы занимают
все
тактов информационные символы занимают
все![]() ячеек регистра. Затем ключ переводится
в положение 2, и регистр совершает ещеnтактов, при каждом из
которых на выходе появляется очередной
символ кодового слова. Уже при первом
из этих
ячеек регистра. Затем ключ переводится
в положение 2, и регистр совершает ещеnтактов, при каждом из
которых на выходе появляется очередной
символ кодового слова. Уже при первом
из этих![]() тактов в первой ячейке формируется
проверочный символ. За
тактов в первой ячейке формируется
проверочный символ. За![]() тактов весь кодовый вектор сформирован,
тактов весь кодовый вектор сформирован,![]() символов выданы на выход, а остальные
символов выданы на выход, а остальные![]() символов находятся в регистре. Ключ
возвращается в положение 1, и в регистр
вводится
символов находятся в регистре. Ключ
возвращается в положение 1, и в регистр
вводится![]() информационных символов следующего
вектора, а оставшиеся в регистре
информационных символов следующего
вектора, а оставшиеся в регистре![]() символы предыдущего вектора выводятся
на выход кодера.
символы предыдущего вектора выводятся
на выход кодера.
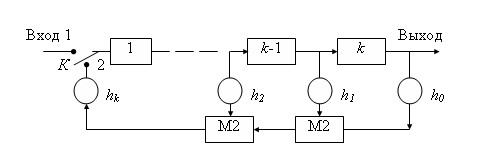
Рис. Кодер ck-разрядным регистром, реализованный по полиномуh(x)