Исходные данные для выполнения расчёта

показатель	Цифра зачетной книжки
	0	1	2	3	4	5	6	7	8	9
L1, м	4	6	8	10	12	5	7	9	11	3
L2, м	6	8	6	8	10	8	7	6	8	5
DН, мм	133	159	194	219	273	108	89	76	57	108
R, мм	500	600	600	650	650	500	350	350	200	500

При расчёте труб на компенсацию тепловых удлинений с гибкими П и S образными компенсаторами или участками самокомпенсации определяют такие их габариты, при которых продольные изгибающие компенсационные напряжения, возникающие при упругой деформации труб, не превышают допускаемых.

Схема расчётного участка дана на рис.5.2.

Рис. 5.1. Эпюра изгибающих моментов Г-образного участка трубопровода

Рис. 5.2. Г-образный участок трубопровода с углом поворота 90^оС (с учётом гибкости отвода)

Расчёт производят по формулам:

Приведённая длина осевой линии участка трубопровода

L_пр= l₁+ l₂+1,57Rk, м (5.1.)

где R – радиус оси отвода в м

k – коэффициент гибкости для гнутых гладких отводов определяют по следующим формулам:

при h≤1 – по формуле Кларка и Рейснера:

(5.2)

h – геометрическая характеристика гибкости трубы;

при h>1 – по формуле Кармана:

(5.3)

Геометрическую характеристику гибкости трубы определяют по формуле:

h = sR/r (5.4.)

где s – номинальная толщина стенки трубы в мм;

r_ср - средний радиус трубы в мм;

R – радиус оси гнутой трубы или условный радиус сварного отвода в мм;

Средний радиус трубы определяют по формуле:

r_ср мм (5.5)

Величина коэффициента k может быть определена по графику на рис. 5.3.

Координаты упругого центра тяжести:

(5.6)

(5.7)

Центральные моменты инерции относительно осей х_о и у_о

м³; (5.8.)

м³; (5.9)

Центральный центробежный момент инерции относительно осей х_о и у_о

І_хуо= 0,072R³k – L_прх_оу_о м³; (5.10)

Расчётные тепловые удлинения вдоль осей х и у:

Δх = αΔt(l₂+R) мм; (5.11.)

Δу = -αΔt(l₁+R) мм; (5.12.)

где α – коэффициент линейного расширения трубной стали в мм/м град (определяем по табл. 4.3);

Δ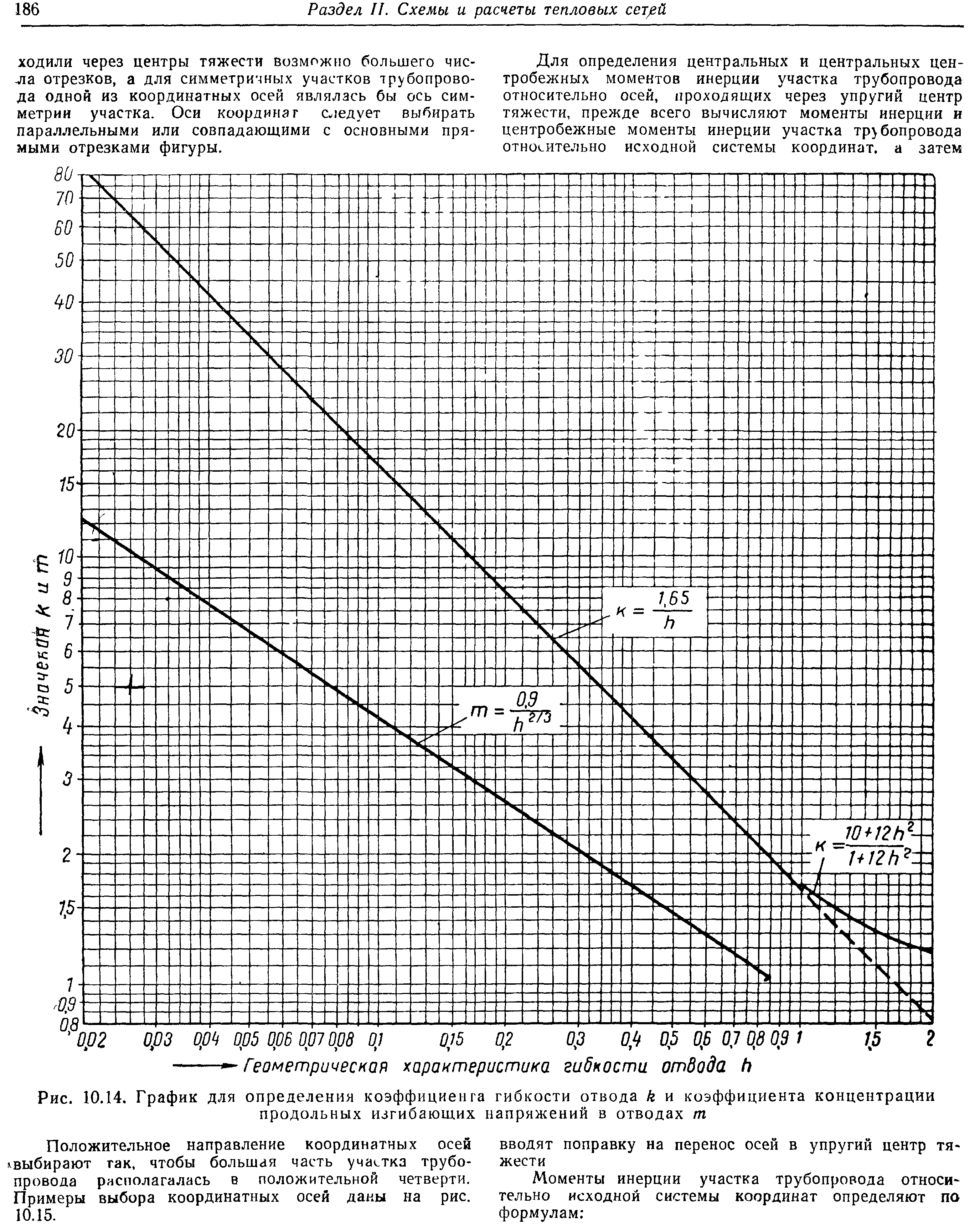t – расчётная разность температур между максимальной температурой теплоносителя и расчётной температурой наружного воздуха для проектирования отопления.

Рис. 5.3. График для определения коэффициента гибкости отвода k и коэффициента концентрации продольных изгибающих напряжений в отводах m

Силы упругой деформации, возникающие в трубопроводе при компенсации теплового удлинения, рассматривают в виде двух составляющих, направленных по осям х и у и определяют по формулам:

Н (5.13.)

Н (5.14.)

где І - момент инерции поперечного сечения стенки трубы при номинальной толщине стенки трубы в см⁴ (определяем по приложению 4) или по формуле см⁴;

где D_Н,В - соответственно наружный и внутренний диаметр трубопровода в мм (D_В ⁼ D_Н- 2S)

Е – модуль упругости трубной стали в кгс/см² (определяем по табл. 4.3);

Равнодействующую сил упругой деформации, определяют по формуле:

Р=Н (5.15.)

Максимальный изгибающий момент на прямом отрезке

при l₁≤l₂ в точке А

М_макс=( l₁+R - у_о)Р_х+х_оР_у Нм; (5.16.)

при l₁≥l₂ в точке В

М_макс= - ( l₂+R-х_о)Р_у- у_о Р_х Нм; (5.17.)

Максимальный изгибающий момент на гнутом отрезке в точке С (середина дуги)

М= - (у_о – 0,293R) Р_х+( х_о – 0,293R)Р_у Нм; (5.18.)

Изгибающие компенсационные напряжения на прямых участках трубопроводов в сварных и крутоизогнутых отводах определяют по формуле

Н/м² (Па) (5.19.)

Где W – момент сопротивления поперечного сечения стенки трубы при номинальной толщине стенки трубы в см³ определяется по формуле:

(5.20)

Изгибающие компенсационные напряжения в гнутых гладких отводах определяют по формуле

Н/м² (Па) (5.21.)

Где m коэффициент концентрации продольных изгибающих напряжений в отводах. Для гнутых гладких отводов определяют по формуле:

(5.22.)

Или по графику рис. 5.3. и учитывают только при значениях m больших единицы (при h<0,85).

Знак «минус» у изгибающего момента в точке показывает только направление этого момента и при определении напряжений не учитывается

Величины изгибающих компенсационных напряжений, полученные по формулам не должны превышать допускаемого изгибающего компенсационного напряжения, полученного по расчёту на прочность (в приближённых расчётах можно принимать σ_доп≤35 МПа).

На поворотах труб расстояния между опорами рекомендуется принимать не более 0,67 от допустимого расстояния на прямом участке трубы, а на участках последней и предпоследней опор до поворота или гибкого компенсатора – не более 0,82

Приложение 1