3. Умови Куна-Таккера

 

У попередньому розділі було встановлено, що множники Лагранжа можна використовувати при побудові критеріїв оптимальності для задач оптимізації з обмеженнями у вигляді рівностей. Кун і Таккер узагальнили цей підхід на випадок загальної задачі нелінійного програмування з обмеженнями, як у вигляді рівностей, так і у вигляді нерівностей. Розглянемо таку загальну задачу нелінійного програмування: мінімізувати (0) при обмеженнях (1) (2) Визначення: Обмеження у вигляді нерівності називається активним, або зв'язує, в точці , Якщо , І неактивним, або несвязивающім, якщо Якщо існує можливість виявити обмеження, які неактивні в точці оптимуму, до безпосереднього виконання завдання, то ці обмеження можна виключити з моделі і тим самим зменшити її розміри. Основна складність полягає при цьому в ідентифікації неактивних обмежень, що передує рішенню завдання. Кун і Таккер побудували необхідні і достатні умови оптимальності для задач нелінійного програмування, виходячи з припущення про диференційовності функцій . Ці умови оптимальності, широко відомі як умови Куна-Таккера, можна сформулювати у вигляді задачі знаходження рішення деякої системи нелінійних рівнянь і нерівностей, або, як іноді кажуть, завдання Куна-Таккера.

3.1. Умови Куна-Таккера і завдання Куна-Таккера

Знайти вектори , Що задовольняють таким умовам (3) (4) (5) (6) (7) Перш за все проілюструємо умови Куна - Таккера на прикладі. Приклад 3 Мінімізувати при обмеженнях Рішення. Записавши цю задачу у вигляді задачі нелінійного програмування (0) - (2), отримаємо Рівняння (3), що входить до складу умов Куна-Таккера, приймає наступний вигляд: звідки Нерівності (4) і рівняння (5) завдання Куна - Таккера в даному випадку записуються у вигляді Рівняння (5.16), відомі як умова доповнює нежорсткої, приймають вигляд Зауважимо, що на змінні і накладається вимога неотрицательности, тоді як обмеження на знак відсутня. Таким чином, цього завдання умови Куна-танкера записуються в наступному вигляді:

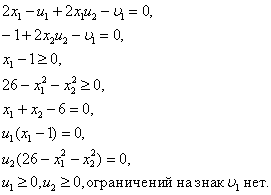
3.2. Інтерпретація умов Куна - Таккера

Для того щоб інтерпретувати умови Куна - Таккера, розглянемо завдання нелінійного програмування з обмеженнями у вигляді рівностей: мінімізувати при обмеженнях Запишемо умови Куна-Таккера (8) (9) Далі розглянемо функцію Лагранжа для задачі нелінійного програмування з обмеженнями у вигляді рівностей Для цієї функції умови оптимальності першого порядку записуються у вигляді 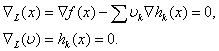Неважко бачити, що умови Куна-Таккера (8) і (9) збігаються з умовами оптимальності першого порядку для задачі Лагранжа. Розглянемо завдання нелінійного програмування з обмеженнями у вигляді нерівностей: мінімізувати при обмеженнях Запишемо умови Куна-Таккера 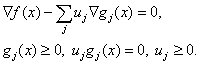Відповідна функція Лагранжа має вигляд Умови оптимальності першого порядку записуються як 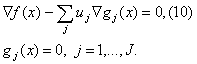Зауважимо, що - Множник Лагранжа, відповідний обмеження . Раніше було показано, що представляє неявну ціну, асоційовану з обмеженням ; Іншими словами, величина відображає зміну мінімального значення цільової функції , Що викликається одиничним збільшенням правій частині - Го обмеження. Якщо припустити, що - Е обмеження є неактивним (тобто З іншого боку, якщо -Е обмеження активне (тобто ), То відповідна неявна ціна не обов'язково дорівнює нулю, однак , Так як . Таким чином, для всіх значень . Для того щоб визначити знак (Неявній ціни, асоційованої з обмеженням ), Слід збільшити праву частину обмеження від 0 до 1. Ясно, що при цьому область допустимих рішень звужується, оскільки будь-яке рішення, яке задовольняє обмеження , Автоматично задовольняє нерівності . Отже, розміри допустимої області зменшуються, і мінімальне значення поліпшити неможливо (так як взагалі воно може тільки зростати). Іншими словами, неявна ціна , Асоційована з -М обмеженням, повинна бути неотрицательной, що відповідає умовам Куна-Таккера.