5.3.4 Нормальное распределение
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается дифференциальной функцией
.
(5.23)
Нормальное распределение определяется двумя параметрами: а и . Достаточно задать эти параметры, чтобы задать нормальное распределение. Вероятностный смысл этих параметров таков: а – математическое ожидание, – среднее квадратичное отклонение нормального распределения.
График дифференциальной функции нормального распределения называют нормальной кривой или кривой Гаусса (рис. 5.1).
Рис. 5.1.
При любых значениях параметров а и площадь, ограниченная нормальной кривой и осью х, остается равной единице.
Выясним, как влияют на форму и расположение нормальной кривой значения параметров а и .
Графики функций f(x) и f(x – а) имеют одинаковую форму; сдвинув график f(x) в положительном направлении оси х на а единиц масштаба при a > 0, или в отрицательном направлении при а < 0, получим график f(x – а). Отсюда следует, что изменение величины параметра а (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси х: вправо, если а возрастает, и влево, если а убывает.
По-иному обстоит дело, если изменяется параметр : С возрастанием максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси х; при убывании нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси у.
На рис. 5.2 изображены нормальные кривые при различных значениях и а = 0. Чертеж наглядно иллюстрирует, как изменение параметра сказывается на форме нормальной кривой.
При а
= 0 и
= 1
нормальную кривую
называютнормированной.
Рис. 5.2. Семейство нормальных кривых распределения
σ = 1; 1,5; 3; 7,5.
Для проверки нормальности распределения случайной величины на практике часто применяют правило трёх сигм.
Сущность правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратичного отклонения.
Если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то имеются основания предполагать, что изучаемая величина распределена нормально.
При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. С этой целью вводят специальные характеристики, в частности, асимметрию и эксцесс. Для нормального распределения эти характеристики равны нулю. Поэтому, если для изучаемого распределения асимметрия и эксцесс имеют небольшие значения, то можно предположить близость этого распределения к нормальному. Наоборот, большие значения асимметрии и эксцесса указывают на значительное отклонение от нормального.
Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратичного отклонения
.
(5.24)
Асимметрия положительна, если “длинная часть” кривой распределения расположена справа от математического ожидания (рис. 5.3, а); асимметрия отрицательна, если “длинная часть” кривой расположена слева от математического ожидания (рис. 5.3, б).
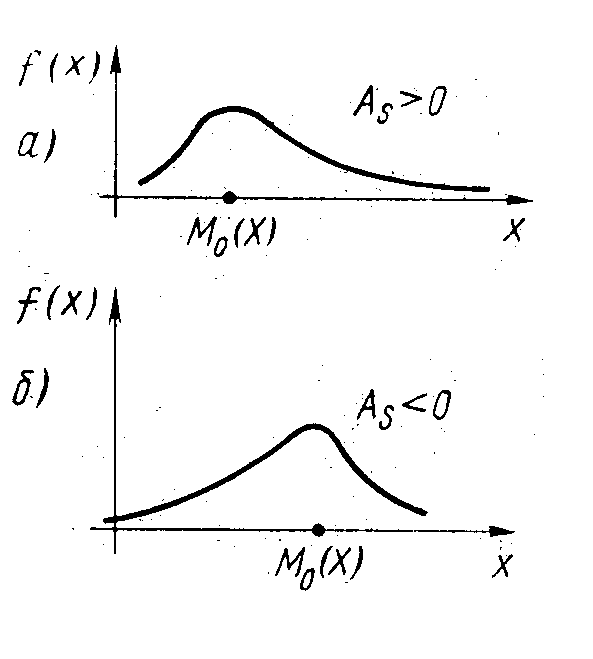
Рис. 5.3.
Для оценки «крутости», т.е. большего или меньшего подъема кривой теоретического распределения по сравнению с нормальной кривой, пользуются характеристикой, называемой эксцессом.
Эксцессом теоретического распределения называют характеристику, которая определяется равенством
.
(5.25)
Для нормального
распределения
,
и, следовательно, эксцесс равен нулю.
Поэтому, если эксцесс некоторого
распределения отличен от нуля, то кривая
этого распределения отличается от
нормальной кривой: если эксцесс
положительный, то кривая имеет более
высокую и «острую» вершину, чем нормальная
кривая (рис. 5.4, а); если эксцесс
отрицательный, то сравниваемая кривая
имеет более низкую и «плоскую» вершину,
чем нормальная кривая (рис. 5.4, б). При
этом предполагается, что нормальное и
теоретическое распределения имеют
одинаковые математические ожидания и
дисперсии.
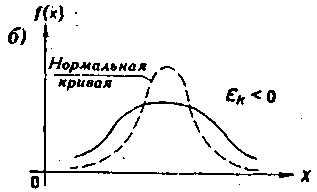
Рис. 5.4.