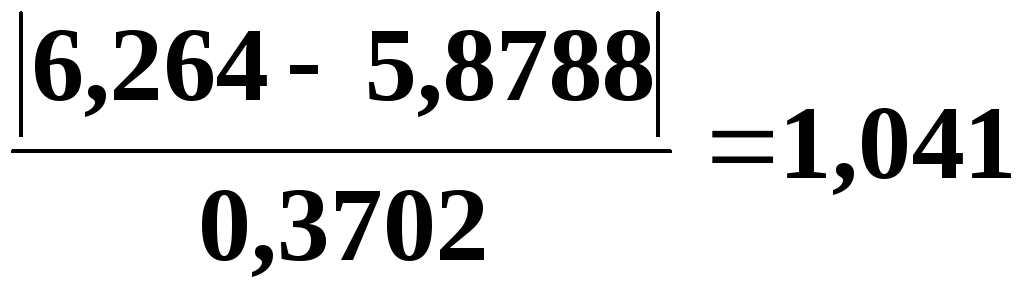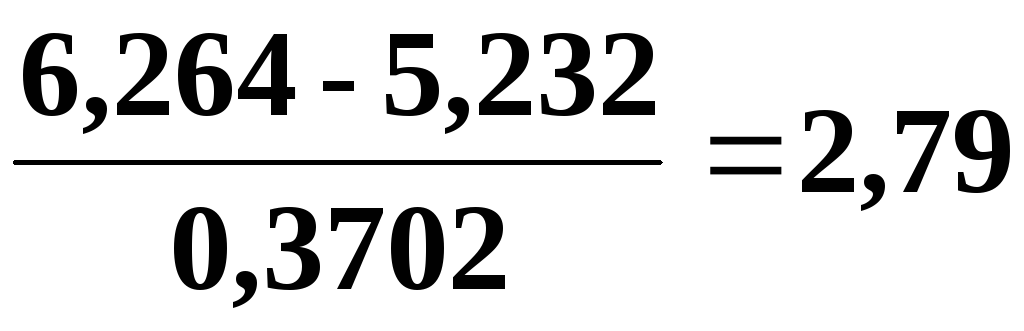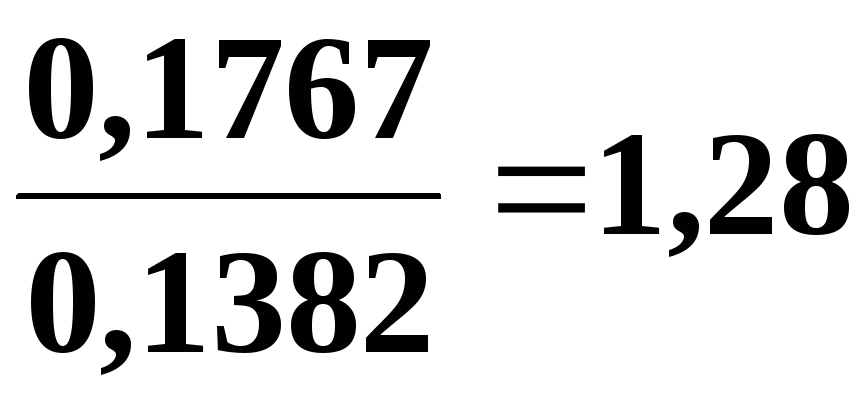5.6.1 Проверка наличия промахов в выборках
Проверку гипотезы
о наличии грубых ошибок (промахов) при
определении плотности прессовок
выполняем путём сопоставления величин
отношений 
в выборках с табличным значением
максимального (критического) относительного
отклонения 
.
Для проверки наличия промахов используем первую и пятую позиции табл. 5.4.
При
объёме выборок 
=
8
и 
= 6 табличная
величина
составляет
2,172. Сопоставление
рассматриваемых параметров представлено
в табл. 5.5.
Таблица 5.5
Данные для проверки гипотезы о наличии промахов при определении плотности прессовок
|
Выборка |
Расчёт
|
Вывод |
|
1
|
|
Выборка промахов не имеет |
|
2 |
|
Выборка промахов не имеет
|
|
3 |
|
Выборка промахов не имеет |
Итак, промахов
в выборках не обнаружено, все значения
,
приведенные в табл. 5.3., доброкачественны
и пересчёту не подлежат.
5.6.2 Определение интервальных оценок плотности прессовок
Вычисляем значения
.
При
=0,05
и 
=8
табличное
значение 
=
2,31.
В таблице 5.6 приведены интервальные оценки плотности прессовок из порошка никеля при давлениях прессования Р1, Р2 и Р3.
Таблица 5.6
Интервальные оценки плотности прессовок
|
Выборка |
|
|
|
1 |
0,1562 |
0,1912 ± 0,1562 |
|
2 |
0,3023 |
0,3702 ± 0,3023 |
|
3 |
0,1443 |
0,1767 ± 0,1443 |
±
5.6.3 Проверка гипотезы о статистической значимости различия плотности прессовок, полученных при различных давлениях прессования
Если 
,
то
различия сравниваемых плотностей
прессовок статистически значимы.
При 
=0,05
и 
=
=
=8
=14
и 
=
2,15.
Проверяем гипотезу
о статистической значимости различия
между значениями плотностей 
и
.
где
Так как 3,139
> 2,15, то
гипотеза о статистической значимости
различия плотностей
и 
принимается.
Проверяем гипотезу
о статистической значимости различия
между значениями плотностей 
и
.
где
Так как 1,122
< 2,15, то
гипотеза о статистической значимости
различия плотностей 
и 
непринимается.
Проверяем гипотезу
о статистической значимости различия
между значениями плотностей 
и
.
где
Так как 6,793
> 2,15, то
гипотеза о статистической значимости
плотностей
и 
принимается.
5.6.4 Проверка нормальности распределения ошибок измерений плотности в выборках
В таблице 5.7.
приведены результаты необходимых
расчётов для проверки гипотезы о
нормальном распределении ошибок
измерений плотности прессовок в выборках.
Согласно справочным данным, нижняя и
верхняя границы отношения 
равны 2,50
и 3,999,
соответственно.
Таблица 5.7
Данные для проверки гипотезы о нормальном распределении ошибок измерений плотности прессовок
|
Выборка |
|
|
|
|
|
1
|
|
|
2,05 |
0,99 |
|
2 |
|
|
2,22 |
0,44 |
|
3 |
|
|
2,53 |
0,22 |
Согласно данным, приведённым в табл. 5.7, можно принять гипотезу о нормальном распределении ошибок измерения плотности прессовок в выборках 1-3.
Действительно:
отношения исправленных стандартных и среднеарифметических отклонений Sиmв выборках близки по величине к 1,25;
отношения размахов варьирования R к выборочным стандартным отклонениям S находятся внутри интервала между нижней и верхней критическими границами при выбранном уровне значимости α = 0,05;
отношение выборочных значений коэффициентов асимметрии
и эксцесса 
к их стандартным ошибкам 
и 
меньше
критических, т.е. 3
и 5,
соответственно.