
- •Содержание
- •ПредислоВие
- •Введение
- •1. Основные понятия и принципы автоматического управления
- •Понятие об управлении и регулировании
- •1.2. Объект автоматического управления. Алгоритм управления
- •1.3. Принципы автоматического управления
- •1.3.1. Принцип разомкнутого управления
- •1.3.2. Принцип управления по возмущению
- •1.3.3. Принцип управления по отклонению
- •1.4. Классификация автоматических систем
- •2. Модели линейных асу и их элементов
- •2.1. Понятие о моделях асу
- •2.2. Общие сведения о статических и динамических характеристиках асу и ее звеньев
- •2.3. Передаточная функция
- •2.4. Переходная и весовая функции
- •2.5. Частотная передаточная функция
- •Воспользовавшись известными записями формулы Эйлера
- •2.5. Типовые динамические звенья
- •2.5.1. Апериодическое звено первого порядка
- •2.5.2. Звенья второго порядка
- •Апериодическое звено второго порядка
- •Колебательное звено
- •Консервативное звено
- •2.5.3. Интегрирующее звено
- •3. Устойчивость линейных асу
- •3.1. Основные понятия устойчивости
- •3.2. Связь устойчивости с корнями характеристического уравнения
- •3.3. Критерии устойчивости
- •Литература
2.4. Переходная и весовая функции
Изображение выходной величины непосредственно следует из определения передаточной функции:
![]() . (2.8)
. (2.8)
Переходная
функция может быть найдена с применением
обратного преобразования Лапласа при
![]()
![]() . (2.9)
. (2.9)
Подставив (2.8) в (2.9), получим
![]() .
.
Если
входной сигнал ![]() ,
то его изображение
,
то его изображение  и тогда
и тогда
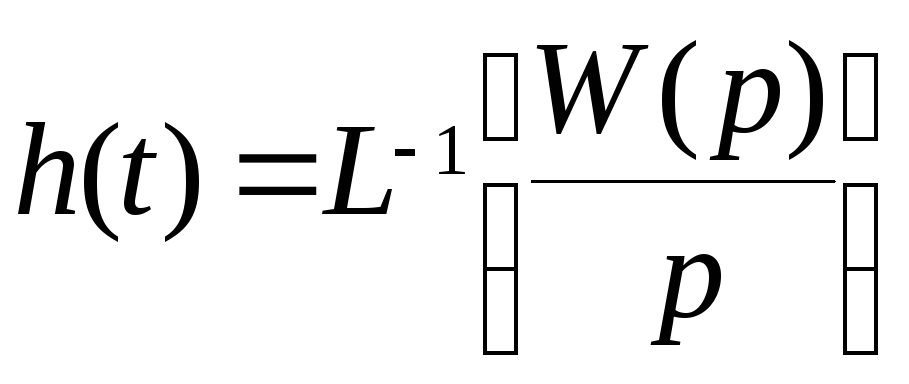 .
.
Весовую
функцию ![]() определяют также с применением обратного
преобразования Лапласа при
определяют также с применением обратного
преобразования Лапласа при ![]()
![]() .
.
Так
как ![]() ,
a
,
a ![]() ,
то изображение входа
,
то изображение входа ![]() и следовательно
и следовательно
![]() .
.
Это
равенство дает второе определение
передаточной функции: это изображение
выходной величины при нулевых начальных
условиях при подаче на вход ![]() функции.
функции.
Таким образом, импульсная переходная функция (функция веса) есть обратное преобразование Лапласа передаточной функции
![]() .
.
2.5. Частотная передаточная функция
Как
уже отмечалось в разд. 2.2, частотные
характеристики это графики, показывающие
зависимость отношения амплитуд
![]() на
выходе и входе звена и сдвига фазы
на
выходе и входе звена и сдвига фазы![]() от
частоты при поступлении на вход
гармонического сигнала
от
частоты при поступлении на вход
гармонического сигнала![]() и установившемся
сигнале на выходе
и установившемся
сигнале на выходе ![]() .
.
Воспользовавшись известными записями формулы Эйлера
![]() (2.10)
(2.10)
и
![]() , (2.11)
, (2.11)
можем представить синусоидальный сигнал выражением
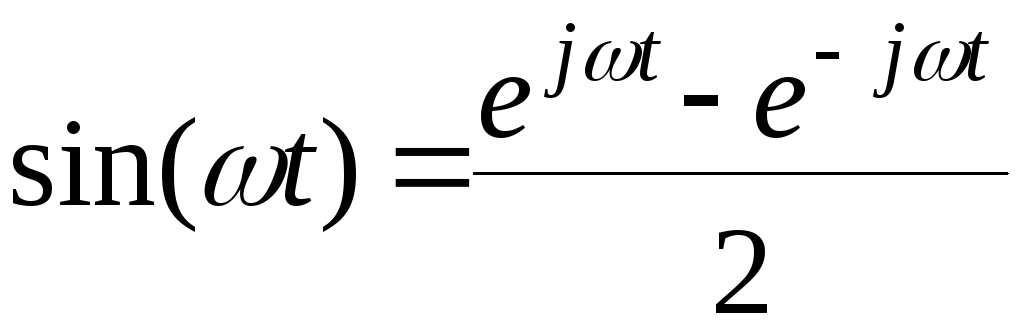 .
.
Тогда входную и выходную переменные можно представить в виде суммы экспоненциальных функций
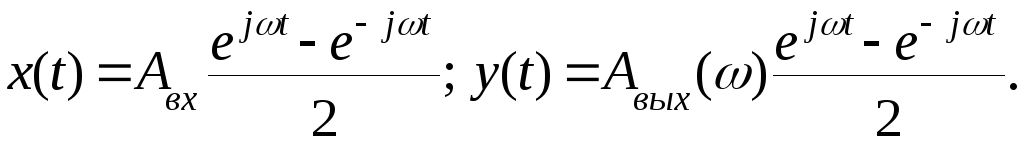
На основании принципа суперпозиции прохождение через звено каждой составляющей сигнала можно рассматривать отдельно. Поэтому, обычно, пользуются символической записью гармонической функции
![]()
Тогда ![]() (2.12)
(2.12)
![]() (2.13)
(2.13)
Отношение выходного сигнала к входному называется частотной передаточной функцией (её иногда называют просто частотной)

Пусть, например, звено описывается уравнением
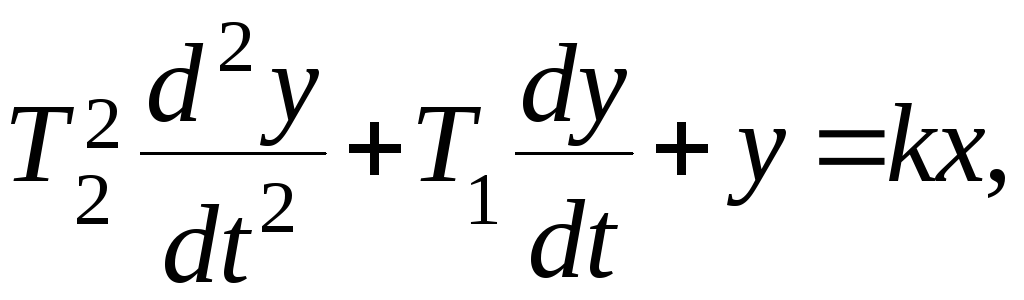 (2.14)
(2.14)
которое соответствует передаточной функции
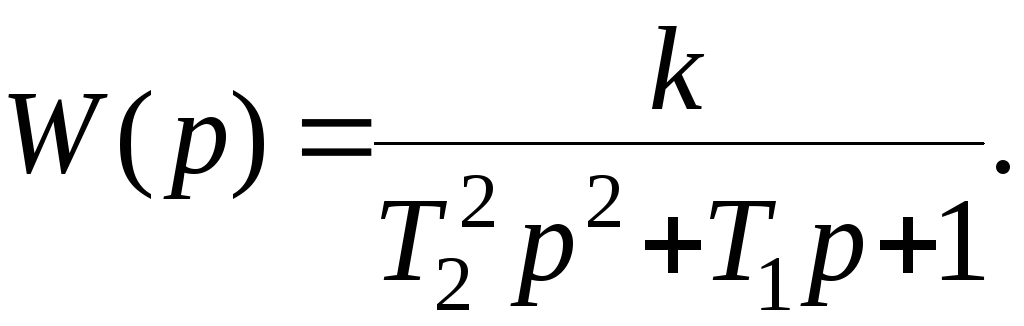
С учетом (2.13) запишем
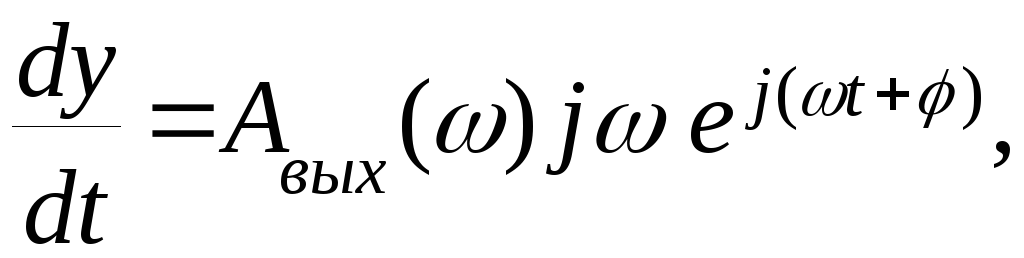
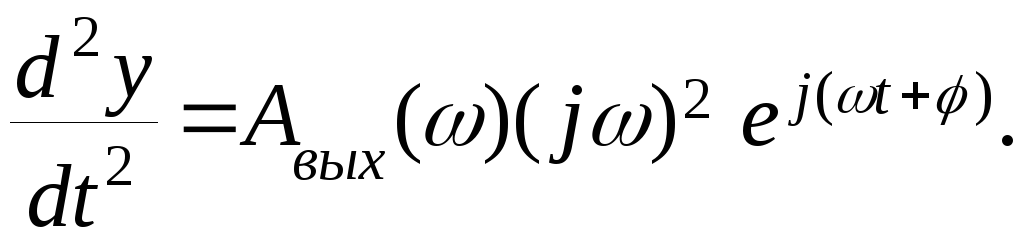
После подстановки этих выражений в уравнение (2.14) получим
![]()
Отсюда частотная функция звена
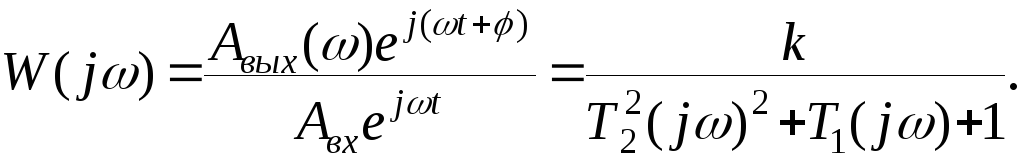
Сравнение
частотной функции с обычной показывает,
что она может быть получена путём
формальной замены оператора![]() на
на![]() .
.
Частотную функцию можно представить в виде
![]() ,
,
или в показательной форме
![]() .
.
В
этих выражениях ![]() и
и ![]() соответственно действительная и мнимая
части частотной функции;
соответственно действительная и мнимая
части частотной функции; ![]() –
модуль частотной функции (обозначают
также
–
модуль частотной функции (обозначают
также ![]() ),
а
),
а ![]() –
её фаза. Легко показать (рис. 2.14), что
модуль можно найти из выражения
–
её фаза. Легко показать (рис. 2.14), что
модуль можно найти из выражения
![]() ,
,
а фазу из выражения
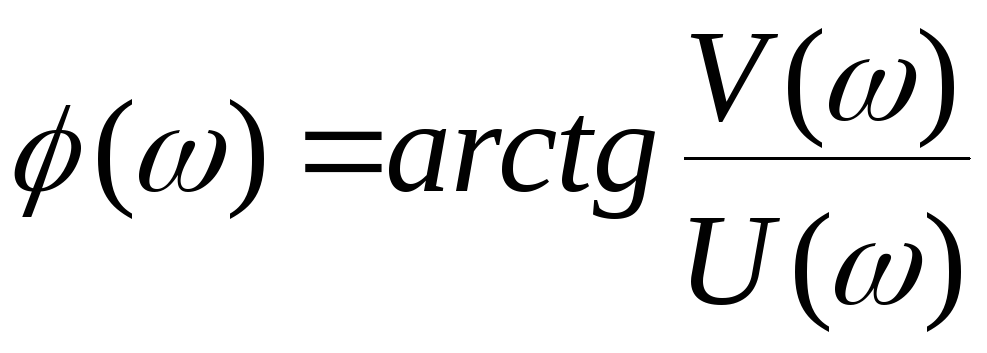 .
.
На
комплексной плоскости (рис. 2.14) частотную
передаточную функцию определяет годограф
вектора
![]() ,
длина (модуль) которого равна
,
длина (модуль) которого равна![]() ,
а аргумент (угол, образованный этим
вектором с действительной положительной
полуосью)
,
а аргумент (угол, образованный этим
вектором с действительной положительной
полуосью) ![]() .
Кривую, которую описывает конец вектора
при изменении частоты от 0 до ∞, называют
амплитудно-фазовой характеристикой
(АФХ). Таким образом, АФХ – это совмещённые
АЧХ и ФЧХ.
.
Кривую, которую описывает конец вектора
при изменении частоты от 0 до ∞, называют
амплитудно-фазовой характеристикой
(АФХ). Таким образом, АФХ – это совмещённые
АЧХ и ФЧХ.

Рис. 2.14. Построение АФХ по частотной функции
Итак, передаточная функция полностью определяет как статические, так и динамические свойства системы (звена). Она показывает, по какому закону тот или иной сигнал, поступивший на вход, преобразуется в выходной сигнал системы или звена.
2.5. Типовые динамические звенья
Любую систему можно представить в виде соединения звеньев – условно выделенных преобразователей сигнала направленного действия. Зная математические модели отдельных звеньев, можно получить модель всей системы.
Направленность действия означает, что сигнал передаётся от входа звена к выходу, а подключение других звеньев не оказывает влияния на свойства звена. Другими словами, включение звена в систему не изменяет его математической модели.
Типовые звенья описываются уравнениями не выше второго порядка, имеют один вход и один выход и являются элементами направленного действия.
Звено не обязательно соответствует функциональному элементу АСУ. Сложный элемент можно представить в виде соединения простых звеньев (не выше 2-го порядка), а соединение простых элементов – объединить в одно звено. Например, несколько последовательно соединённых усилителей заменяют одним с коэффициентом передачи, равным произведению коэффициентов усиления всех усилителей, входящих в соединение.
Рассмотрим вначале наиболее часто встречающиеся типовые звенья, а затем обратимся к особенностям их соединения и правилам преобразования структурных схем.
