3. Найбільше і найменше значення функції

Якщо функція неперервна на відрізку, то вона досягає на ньому найбільше і найменше значення. Їх позначаютьтана відрізкуі називають глобальним максимумом та глобальним мінімумом відповідно. Ці значення можуть досягатися у точках локального екстремуму або на кінцях проміжку (рис. 6).а                                                                     б

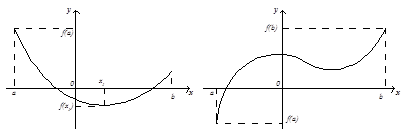в                                                                     г Рис. 6. Найбільше і найменше значення функції на відрізку

Схема знаходження найбільшого і найменшого значень функції на відрізку. 1. Знайти похідну. 2. Визначити всі критичні точки на, тобто точки, в якихабо не існує. 3. Обчислити значення функції в цих критичних точках та на кінцях відрізка і вибрати з них найбільшета найменше. Приклад 3.1. Знайти найбільше і найменше значення функціїна відрізку. á 1.. 2., звідки критичні точки. 3. Значення функції в критичних точкахі на кінцях відрізкаі. Отже,,.

4. Опуклість і увігнутість функції. Точки перегину

Означення 4.1. Функція  називається опуклою (опуклою вгору) на інтервалі , якщо для довільних двох точок  з цього проміжку відрізок, що з’єднує точки  і , розміщений під графіком цієї функції (рис. 7).

Означення 4.2. Функція  називається увігнутою (опуклою вниз) на інтервалі , якщо для довільних двох точок  з цього проміжку відрізок, що з’єднує точки  і , розташований над графіком цієї функції (рис. 8).

           Рис. 7.Опукла функція                        Рис. 8. Увігнута функція

Теорема 4.1. (достатня умова опуклості та увігнутості функції). Нехай функція  двічі диференційована на інтервалі . Тоді: 1)якщо  на , то функція увігнута на цьому інтервалі; 2) якщо  на , то функція опукла на цьому інтервалі. Означення 4.3. Точкою перегину графіка неперервної функції називається точка, яка відокремлює інтервали, на яких функція опукла і увігнута.

Теорема 4.2. (ознака точки перегину). Якщо  і , переходячи через точку , змінює знак, то  є точкою перегину графіка функції .

Приклад 4.1. Визначити інтервали опуклості та увігнутості, точки перегину графіка функції . á Знайдемо другу похідну:,. Корені рівняння–та.на інтервалахі, отже, на цих інтервалах функція увігнута;

Рис. 9. Точки перегину функції

на інтервалі , отже, функція на ньому опукла, аіє точками перегину (рис. 9). Значення функції в точках перегину.

5. Асимптоти графіка функції

Досі ми розглядали характерні точки графіка функції: точки екстремуму, точки перегину. Тепер розглянемо характерні лінії.

Означення 5.1. Асимптотою графіка функції  називається пряма, яка має таку властивість: відстань від точки  до цієї прямої стає як завгодно малою за необмеженого віддалення точки графіка від початку координат.

Розрізняють вертикальні (рис. 10, а) та похилі (зокрема горизонтальні) (рис. 10, б, в) асимптоти. а) вертикальна асимптота;                        б) похила асимптота;в) горизонтальна асимптота

Рис. 10. Асимптоти графіка функції

Визначення асимптот графіка функції ґрунтується на таких твердженнях.

Теорема 5.1. Пряма  є вертикальною асимптотою графіка функції , якщо  або .

Наприклад, графік функції має вертикальні асимптоти(див. додаток). Теорема 5.2.Якщо існують скінченні границі  і , то  є похилою асимптотою графіка функції .

Якщо обидві границі скінченні лише коли , то пряма  є відповідно тільки правосторонньою (лівосторонньою) похилою асимптотою графіка функції .

Приклад 5.1. Визначити асимптоти графіка функції . á З області визначення  “випадає” точка. Знайдемо границю функції, якщо:, звідки– вертикальна асимптота. Визначимо похилу асимптоту... Отже,– похила асимптота графіка функції.