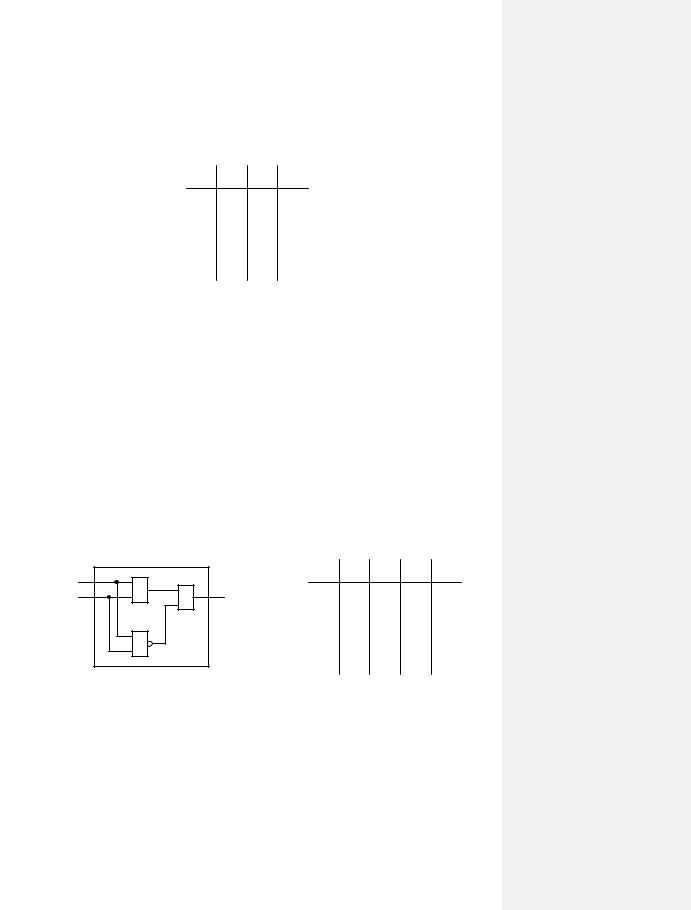
1.5.3Побудова суматора
Розглянемо будову простого однорозрядного суматора. Щоб краще зрозуміти його роботу, пройдемо поступово весь шлях, як у п. 1.3.2У результаті ми повинні отримати схему, якій відповідає таблиця істинності наведена на рис. 2.37.
Рис. 2.37. Таблиця істинності півсуматора
Як видно у схеми повинні бути два входи ( та ) і два виходи ( та , де – це ознака перенесення в старший розряд).
Схема півсуматора
Почнемо з простої схеми (рис. 2.14), у якої є тільки один вихід ( ) та дотримано лише перші три правила таблиці істинності. Порівняння з розглянутими вище логічними елементами показує, що схемі (рис. 2.14) відповідає логічний елемент АБО (рис. 2.28).
Ускладнимо завдання й спробуємо сформувати логічний еквівалент схеми (рис. 2.15). Необхідно так модифікувати схему (рис. 2.28), щоб у випадку наявності сигналів на обох його входах, на виході сигналу не було. Цього можна досягнути логічним перемноженням сигналів, отриманих на виходах елементів АБО та І-НІ (рис. 2.28).
Рис. 2.38. Схема, що відповідає усім правилам логічного додавання (а) та її таблиця істинності (б)
Якщо переглянути таблицю істинності різних логічних функцій (табл. 2.8), видно що складена нами схема еквівалентна логічній функції ВИКЛЮЧНЕ АБО (рис. 2.35). Саме тому цей елемент є основним у схемах суматорів.
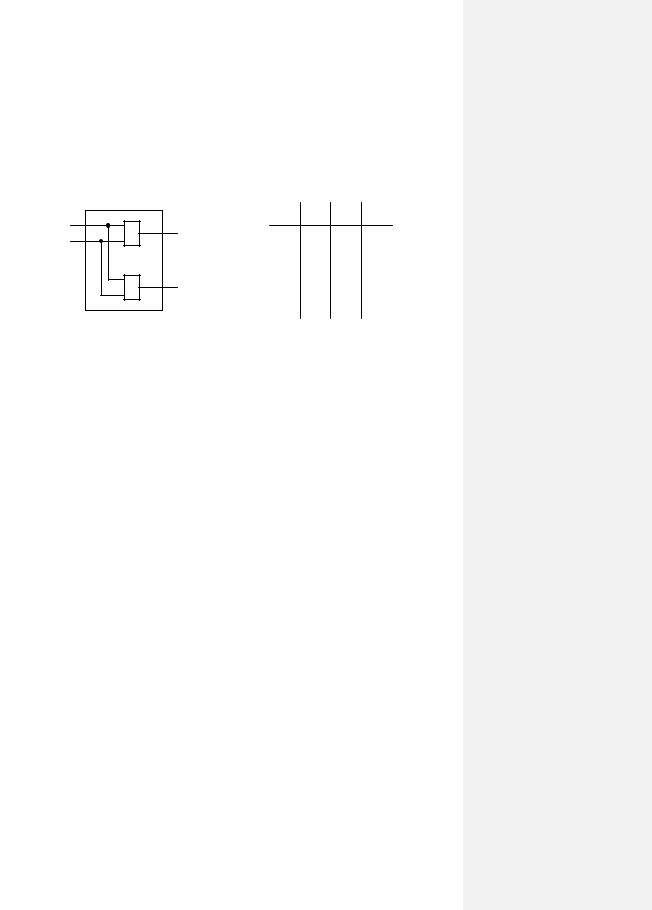
Тепер залишається скласти еквівалент схеми (рис. 2.16), що однозначно відповідає таблиці істинності (рис. 2.37). Цю схему називають півсуматор і її можна скласти з двох логічних елементів:
•ВИКЛЮЧНЕ АБО – вихід цього елементу дасть результат суми,
•І – вихід цього елементу дасть ознаку перенесення.
Повністю схема півсуматора та його таблиця істинності наведені на рис. 2.39.
Рис. 2.39. Схема півсуматора та таблиця істинності
Схема суматора
Як зазначалося в п. 1.3.2у суматорі, окрім двох доданків необхідно також враховувати одиницю перенесення з молодшого розряду в старший. Тому схема суматора повинна містити не два входи а три. Таблиця істинності такого елементу наведена на рис. 2.40.
x1 |
x2 |
c |
|
y |
p |
|
|
|
|
|
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
Рис. 2.40. Таблиця істинності суматора
Схема, що відповідає такій таблиці істинності наведена на рис. 2.41. Як видно у його склад входять два півсуматори та один елемент АБО