Як і у звичайній математиці, логічні формули можна певним чином перетворювати. Деякі перетворення логічних формул подібні на перетворення формул у звичайні алгебрі (винесення спільного множника за дужки, використання знаків тощо). Тут застосовують такі правила:

•правило комунікативності – в операціях логічного множення чи додавання змінні можна переставити місцями,

•правило асоціативності – якщо у виразі використовуються лише операції логічного множення чи логічного додавання то можна знехтувати дужками чи довільно переставляти змінні,

•правило дистриб’ютивності – в алгебрі висловлювань можна

виносити за дужки як спільні множники так і спільні доданки. Інші логічні перетворення базуються на властивостях, які відсутні у

звичайній алгебрі. Основними з них є

•розподілювальний закон для кон’юнкції,

•закон поглинання,

•закон склеювання,

•правила де Моргана.

Усі ці правила необхідні для спрощення вихідних логічних рівнянь з метою побудови найпростішої схеми, покликаної реалізовувати цю функцію. Детально правила перетворювання логічних функцій та їх практичного застосування для побудови обчислювальних пристроїв вивчаються в курсі схемотехніки.

1.5.2Основні логічні елементи

Оскільки в основі виконання основних математичних операцій ЕОМ лежать логічні функції, значить технічно основні блоки ЕОМ повинні складатися із елементів, що реалізують ці функції. Такими елементами є десятки і сотні тисяч логічних вентилів (логічних пристроїв), об’єднаних згідно з правилами та законами (аксіомами) логічної алгебри в цілісні схеми.

Логічний вентиль працює за принципом крану (звідси й назва), відкриваючи чи закриваючи шлях сигналам, згідно з правилами тієї логічної функції, що ним реалізована.

Для реалізації перших двох функцій не потрібні спеціальні апаратні затрати, оскільки перша (константа 0) відповідає розриву кола переда-

наведено на рис. 2.26, а призначений він для розв’язки кіл і узгодження навантажень в схемі.

Рис. 2.26. Схемне позначення та таблиця істинності буфера

На рис. 2.26,а наведене позначення, що використовується у вітчизняній та рекомендовано ГОСТ, а на рис. 2.26,б – що використовується в англомовній літературі.

На рис. 2.26,в наведена таблиця істинності буфера (вона відповідає таблиці істинності логічної функції , табл. 2.7).

Інвертор – функція заперечення

Функцію заперечення реалізує так званий інверсний буфер чи інвертор. Його схемне позначення та таблицю істинності наведено на рис. 2.27 (таблиця істинності відповідає таблиці істинності логічної функції , табл. 2.7).

Рис. 2.27. Схемне позначення та таблиця істинності інвертора

АБО – функція логічного додавання

Функція логічного додавання реалізується логічним елементом АБО. Його схемне позначення наведено на рис. 2.28,а (вітчизняний стандарт) та на рис. 2.28,б (англомовна література), а на рис. 2.28,в наведена його таблиця істинності.

Рис. 2.28. Схемне позначення та таблиця істинності елементу АБО

Як видно сигнал на його виході, що відповідає логічній одиниці, зявляється у випадку, коли аналогічний сигнал присутній хоча б на одному з його входів. Якщо ж на обох входах сигнали нульові, вихід також приймає значення 0.

Слід зауважити, що поняття АБО можна поширити на елементи з входами (рис. 2.29).

Рис. 2.29. Елемент АБО з входами

І – функція логічного множення

Функція логічного множення реалізується логічним елементом І. Його схемне позначення наведено на рис. 2.30.а та на рис. 2.30.б, а на рис. 2.30.в наведена його таблиця істинності.

Рис. 2.30. Схемне позначення та таблиця істинності елементу І

На відміну від схеми АБО на виході елементу І одиничний сигнал з’являється лише у тому випадку, якщо аналогічні сигнали присутні одночасно на його двох входах. Якщо ж хоча б на одному вході елементу І сигнал нульовий, вихід також приймає значення 0.

Як і в попередньому випадку поняття І можна поширити на елементи

звходами.

Елемент АБО-НІ

Графічне позначення елементу, що реалізує функцію АБО-НІ (стрілка Пірса), а також його таблицю істинності зображено на рис. 2.31.

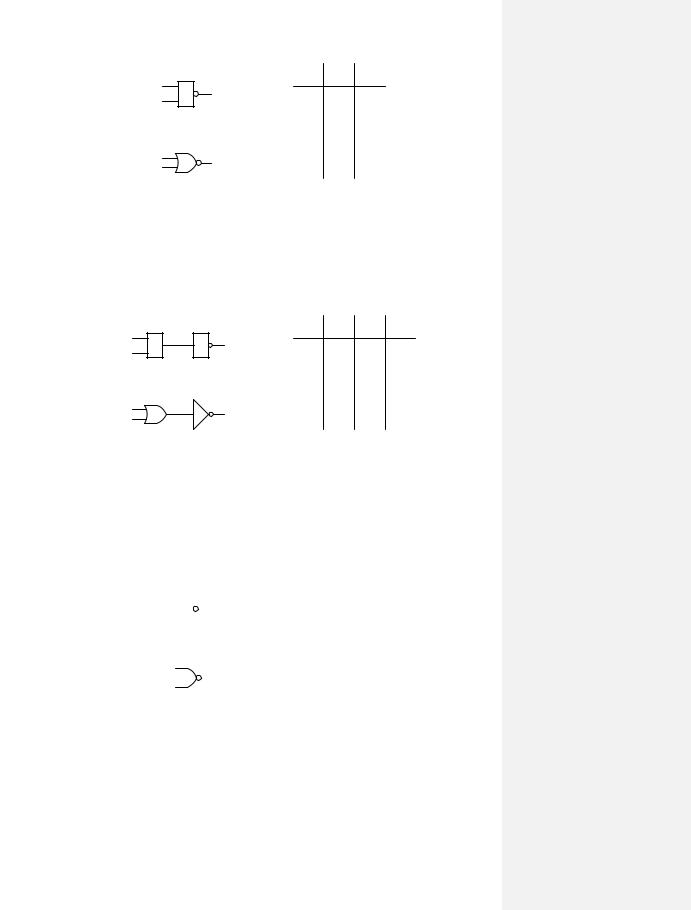
Рис. 2.31. Схемне позначення та таблиця істинності елементу АБО-НІ

Подібно до того як функцію АБО-НІ можна виразити через функції АБО та заперечення

логічний елемент АБО-НІ можна побудувати через два логічні елементи АБО та інвертор (рис. 2.32,а чи рис. 2.32,б).

Рис. 2.32. Побудова елементу АБО-НІ через елементи АБО та інвертор

На рис. 2.32.в наведено таблицю істинності для кожного з виводів схеми (у тому числі й проміжних).

Елемент І-НІ

Графічне позначення елементу, що реалізує функцію І-НІ (штрих Шефера), зображено на рис. 2.33

Рис. 2.33. Схемне позначення та таблиця істинності елементу І-НІ

Цей логічний елемент можна реалізувати через логічні елементи І та інвертор (рис. 2.34)