1.2.2Векторна графіка.
Векторна графіка (також геометричне моделювання чи об’єктноорієнтована графіка) створення зображення з сукупності геометричних примітивів (точок, ліній, кривих, полігонів), тобто об’єктів які можна описати математичним рівнянням.
Тут кожне зображення складається з окремих, незалежних один від одного геометричних об’єктів, які можна редагувати як окремо один від одного так і в комплексі. Кожен об’єкт описується математичною моделлю, що складається з контуру та його внутрішньої області. Кожна з цих складових характеризується своїми параметрами, від яких залежить зовнішній вигляд зображення, – це тип і товщина контурної лінії, вид заповнення внутрішньої області тощо.
Оскільки кожний векторний об'єкт є незалежною системою, його можна переміщати і багато разів змінювати його властивості, зберігаючи при цьому первинну якість і чіткість зображення і не впливаючи на інші об'єкти ілюстрації. Ці властивості роблять векторну графіку дуже зручним інструментом для ілюстративного і тривимірного моделювання, де в процесі роботи часто вимагається створювати окремі об'єкти, видозмінювати їх, компонуючи загальне зображення.
Векторна графіка широко використовується в інженерній та науковій діяльності, тому розглянемо її основи дещо детальніше.
Математичні основи векторної графіки
Векторні об'єкти завжди мають шлях, що визначає їх форму. Шлях уявляє собою маршрут, що з'єднує початкову та кінцеву точку. Якщо шлях є замкненим, тобто кінцева точка співпадає з початковою, об'єкт має внутрішню ділянку, яка може бути заповненою кольором або іншими об'єктами. Всі шляхи містять дві компоненти: сегменти та вузли.
сегмент – окрема частина шляху, може бути як прямою, так і кривою лінією,
вузол – початкова або кінцева точка сегмента.
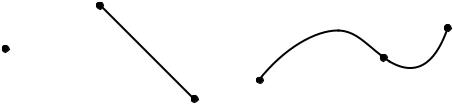
Кожен елемент векторної графіки містить ці основні елементи і дозволяє їх редагування. А основними математичними об’єктами векторної графіки є точка, лінія, сегмент (відрізок) та сплайн.
точка |
лінія |
сплайн |
|
Рис. 1.1. Основні графічні примітиви
Точка – об'єкт на площині, що представляється двома числами відносно початку координат.
Пряма лінія – їй відповідає рівняння
(1.1)
Вказавши параметри та можна створити пряму лінію у відомій системі координат.
Сегмент прямої (відрізок) – для опису потрібно додатково вказати параметри та , відповідно початку та кінця відрізку.
Сплайн. Важливим об’єктом векторної графіки є сплайн. Сплайн – це крива (ІІ чи ІІІ порядку), за допомогою якої описується та чи інша геометрична фігура. На сплайнах побудовані сучасні шрифти TrueType і PostScript.
Крива лінія ІІ порядку – характеризується тим що не має точок перегину і описується рівнянням
(1.2)
Для побудови відрізка кривої додатково потрібні ще два параметри початку та кінця відрізку.
До кривих ліній ІІ порядку відносять еліпси, круги, параболи, гіперболи тощо. Пряма лінія є також випадком кривої ІІ порядку. У свою чергу крива ІІ порядку є частковим випадком кривих ІІІ порядку.
Крива лінія ІІІ порядку – у неї наявні точки перегину, що дозволяє відобразити різноманітні об'єкти. Рівняння кривої ІІІ порядку має вигляд
(1.3)
Для опису відрізка потрібні ще два параметри початку та кінця відрізку.
Криві Без'є. Спрощений вид кривих ІІІ порядку. Метод побудови кривих Без'є заснований на використанні пари дотичних, що проведені до відрізка лінії в його закінченні. На форму кривої лінії впливає кут нахилу дотичної та довжина її відрізка. Таким чином, дотичні відіграють роль віртуальних важелів, за допомогою яких керують формою кривої.
Їх творцем ще у 1968 році став французький вчений, математик і інженер П’єр Без’є. Тоді вони розроблялись для потреб важкої промисловості. П’єру було поставлено завдання: навчитися за допомогою мінімальних машинних ресурсів максимально просто і узагальнено описувати будь-які складні плоскі форми. Це необхідно було для машин з оброблення листового металу, які вирізали з нього необхідні деталі.
Без’є справився не просто добре, а геніально. Його система кривих, базується лише на тригонометричних формулах. Вона виявилась настільки простою і зручною, що лягла в основу не тільки графічних, а й багатьох інших програм.
Математично цю криву описують формулою (параметричне задання)
|
∑ |
|
[ |
] |
|
(1.4) |
де |
– опорні вершини, |
( ) |
|
– поліноми Берштейна, |
||
які є базисними функціями кривої Без’є. |
|
|
|
|
||
|
Існує також рекурсивна формула побудови кривих Без’є |
|
||||
|
|
|
|
|
|
(1.5) |
|
Залежно від значення змінної рівняння розрізняють лінійну, |
|||||
квадратичні та кубічну криву Без’є. У випадку лінійної кривої, коли |
, |
|||||
крива є відрізком від точки |
до точки |
(лінійна |
інтерполяція). Її |
|||
рівняння спрощується до вигляду |
|
|
|
|
|
|
|
|
|
|
[ ] |
|
(1.6) |
|
Квадратична крива Без’є ( |
) задається трьома опорними точками |
||||
, |
та . Її рівняння має вигляд |
|
|
|
|
|
|
|
|
|
[ |
] |
(1.7) |
|
Тут лінія починається у |
точці |
і |
закінчується у точці |
не |
|
проходячи через а точку , яка використовується лише для визначення
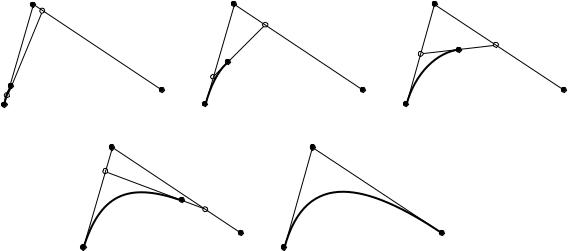
шляху лінії. Графічно це добре видно на рис. 1.2. Тут точка |
призначена |
||||||
лише для побудови |
відрізків |
і |
в межах яких |
будується |
|||
допоміжний відрізок |
. |
|
|
|
|
|
|
а) |
P1 |
б) |
P1 |
|
в) |
P1 |
|
Q1 |
|
|
|
|
|||
|
|
|
Q1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q0 |
|
Q1 |
|
|
|
|
|
B |
|
|
|
|
|
B |
|
|
|
|
|
|
Q0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Q0 |
B |
|
|
|
|
|
|
|
P2 |
|
|
P2 |
|
P2 |
|
|
|
|
|
|
|||
P0 |
|
P0 |
|
|
P0 |
|
|
г) |
P1 |
|
д) |
|
|
||
|
Q0 |
|
|
|
|
B |
Q1 |
|
|
|
P2
P0 |
P0 |
P1 |
P2
Рис. 1.2. Побудова лінії Без’є другого порядку
Крива рисується починаючи з точки (рис. 1.2,а). В міру руху точки по відрізку (який у свою чергу рухається в межах відрізків і ) вимальовується крива (рис. 1.2,б-рис. 1.2,г). Завершений її вигляд
показано на рис 1.2,д.
Відмітимо, що саме сплайни з квадратичних кривих Без'є використовуються для описування форми символів в шрифтах TrueType.
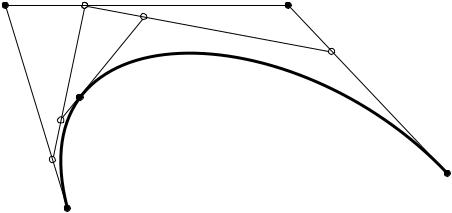
Кубічна крива Без’є ( ) – чотири опорні точки , , та , задані в 2-х чи 3-мірному просторі визначають форму кривої. Рівняння кривої має вигляд
|
|
[ ] |
(1.8) |
|
|
|
|
Тут уже дві точки |
та |
є допоміжними, призначеними лише для |
|
визначення шляху (напрямку руху). Відповідно система допоміжних відрізків та побудова цієї кривої в цілому дещо складніші (рис. 1.3).
|
|
Q |
|
|
|
P |
|
1 |
|
P |
2 |
1 |
|
|
|||
|
|
|
|||
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
1 |
|
Q |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
R0 |
B |
|
|
|
|
Q |
|
|
|
|
|
0 |
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
P |
|
|
|
|
|
0 |
|
|
|
|
Рис. 1.3. Побудова лінії Без’є третього порядку
Найбільше значення мають криві Без’є другого та третього степеня (квадратичні і кубічні). Криві вищих степенів під час оброблення вимагають значно більшого обсягу обчислень й на практиці застосовуються рідше.
Для побудови складних за формою ліній окремі криві Без’є об’єднують послідовно одна з одною в сплайн Без’є. Для цього, щоб забезпечити гладкість лінії у місці з’єднання двох кривих, суміжні опорні точки обох кривих повинні лежати на одній лінії. В програмах векторної графіки подібні фрагменти відомі під назвою шляхів» (path).
Основні примітиви та їх елементи
Зазвичай від користувача приховані математичні основи векторної рафіки. Для цього у спеціалізованих редакторах йому надається набір простих геометричних фігур, так званих примітивів – лінія, дуга, прямокутник, еліпс, ламана тощо.
За допомогою цих примітивів можна рисувати складніші рисунки, для чого певним чином необхідно змінювати параметри базових
примітивів. Ці параметри можна розподілити на просторові, контуру (лінії) та заповнення.
Просторові параметри. В першу чергу тут мова йде про координати окремих точок примітивів (у першу чергу їх початку та кінця) а також про коефіцієнти рівняння, яким вони описані (про що мова йшла вище).
Явно можна задавати лише кординати вершин ліній (це можна зробити як за допомогою мишки так і з клавіатури). Коефіцієнти ж рівняння явно н фігурують, для їх задання примітивам надають спеціальні інструменти – напрямні.
Окрім цього векторні графічні редактори дозволяють застосовувати до примітивів (та до груп примітивів) такі операції як переміщення, обертання, розтягування, відображення, викривлення тощо.
Параметри контуру (лінії). Залежно від можливостей графічного редактора для зміни можуть бути доступні такі параметри:
товщина контуру,
колір контуру,
стиль контуру – неперервна чи перервна (штрихова, штрихпунктирна тощо) лінія,
вибір одного із варіантів кутів та завершень ліній;
вибір стрілок, які будуть розташовані на початку і/чи в кінці ліній,
нахил і форма пера, що формує контур,
Окрім цього сам контур можна розташовувати над чи під заповненням.
Параметри заповнення. За допомогою кривих створюється контур об'єкта, всередині якого може бути заповнення (любий колір, штрихування або зображення). Заповнений об'єкт трактується як єдиний елемент, тобто при змінюванні форми об'єкта, заповнення заповнює всю його внутрішню ділянку.
Заповнення можна розбити на 4 категорії:
однорідне заповнення одним кольором або штрихуванням;
градієнтне, при якому кольори або тіні поступово змінюються (лінійна, радіальна, конічна, прямокутна тощо);
візерункове, при якому об'єкт заповнюється повторювальними зображеннями (двоколірними або повноколірними);
текстурне заповнення – художні зображення.
Цікаво, що текстурне заповнення є заповнення є растровим, таким чином можна поєднувати векторну та растрову графіки.
Текст. Ще одним примітивом у векторних редакторах є текст. Зазвичай до елементів тексту можна застосовувати ті ж ефекти, що й у