
Лекції 9 -10. Похідні та елементи поведінки функцій (монотонність, екстремум, опуклість, кривина). Асимптоти. Загальна схема дослідження функцій за допомогою похідної. Практичні задачі на екстремум
1. Зростання і спадання функцій
Нагадаємо, що функція y = f (x) |
називається зростаючою (спадною) на інтервалі (a; b) , якщо для |
довільних x1, x2 (a;b) при x2 > x1 |
виконується нерівність f (x2 ) > f ( x1 ) ( f (x2 ) < f (x1 )) . |
Теорема 1 (достатня умова монотонності). Припустимо, що функція y = f (x) диференційовна на
(a; b) . Якщо |
′ |
|
|
f (x) зростаюча на (a; b) ; якщо |
f |
′ |
для всіх |
f (x) > 0 для всіх x (a; b) , то |
(x) < 0 |
||||||
x (a; b) , то |
f (x) |
спадна на(a; b) . |
|
|
|
|
|
Зауваження. Якщо |
f ( x) ≡ 0 на (a;b) , то |
f ( x) |
стала на (a;b) . |
|
|
|
|
|
|
′ |
|
|
|
|
|
. |
|
|
|
|
|
|
|
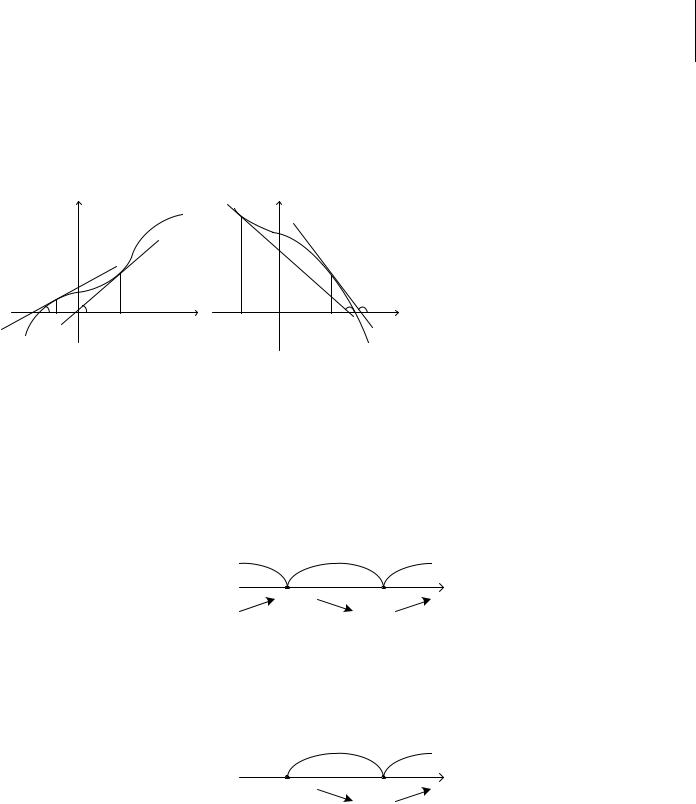
Геометрична інтерпретація умови монотонності функції наведена на рисунку 1. |
|
|
|
||||
y |
|
y |
|
|
|
|
|
α |
α1 |
|
|
|
α1 |
α2 |
2 |
|
x |
|
|
|
x |
x1 0 |
x2 |
x1 |
0 |
x2 |
а) |
б) |
|
Рис. 1. Зростаюча та спадна функція |
Якщо дотичні до кривої на деякому проміжку направлені під гострими кутами до осі абсцис (рис.1 а), то функція зростає, якщо під тупими (рис.1 б), то спадає.
Приклад 1. Знайти інтервали монотонності функцій:
а) y = x3 −6x2 +9x −2 ; |
|
б) y = 2x2 − ln x . |
|
|
|
||||||||||
а) Областю визначення даної функції є множина D( y) = (−∞;+∞). |
|
||||||||||||||
Знаходимо похідну функції: |
y′ = 3x2 −12x +9 . Очевидно, що y′ > 0 при |
x <1 та x > 3 і y′< 0 при |
|||||||||||||
1 < x < 3 , тобто функція зростає на інтервалах (−∞;1) |
і (3;+∞) |
та спадає на інтервалі (1;3) (рис. 2.) |
|||||||||||||
|
|
|
|
y' |
|
+ |
|
|
|
|
- |
|
+ |
|
|
|
|
|
|
y |
|
|
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2. |
|
|
|
б) Функція y = 2x2 − ln x |
визначена на множині D( y) = (0;+∞). |
|
|
||||||||||||
Знаходимо похідну: y |
′ |
1 |
= |
4x2 |
−1 |
= |
(2x −1)(2x +1) |
. |
|
|
|||||
= 4x − x |
|
x |
x |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язуючи нерівності y′ > 0 |
і |
y′< 0 |
методом інтервалів, |
отримаємо, |
що дана функція зростає |
||||||||||
при x |
1 |
; +∞ і спадає при x |
0; |
1 |
|
(рис. 3). |
|
|
|
||||||
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
y' |
|
|
|
|
|
|
- |
|
+ |
|
|
|
|
|
|
y |
|
|
|
|
|
0 |
|
1/2 |
|
|
|
Рис. 3.

2. Екстремум функції
Означення 1. Точка x1 називається точкою максимуму функції f (x) , якщо в деякому околі точки x1 виконується нерівність f (x) ≤ f ( x1 ) (рис. 4).
Означення 2. Точка x2 називається точкою мінімуму функції f (x) , якщо в деякому околі точки x2 виконується нерівність f (x) ≥ f ( x2 ) (рис. 4).
Точки максимуму і мінімуму називаються точками екстремуму функції. Значення функції в точках x1 і x2 називаються відповідно максимумом і мінімумом функції. Максимум і мінімум функції
об’єднуються під загальною назвою екстремуму функції. Екстремум функції часто називають локальним екстремумом, підкреслюючи той факт, що поняття екстремуму пов’язане з достатньо малим околом точки екстремуму. Так що на одному проміжку функція може мати декілька точок максимуму і мінімуму.
y
|
x2 |
x1 0 |
x |
Рис. 4. Екстремуми функції
Теорема 2 (необхідна умова екстремуму). Якщо функція y = f (x) має в точці x0 екстремум, то її похідна в цій точці дорівнює нулю ( f ′(x0 ) = 0) або не існує.
Іншими словами, функція f (x) може мати екстремум тільки в тих точках, в яких похідна
дорівнює нулю або не існує. Точки, в яких похідна функції дорівнює нулю або не існує, називаються критичними (або стаціонарними) точками. Звертаємо увагу на те, що ці точки повинні входити в область визначення функції. Однак легко переконатись, що критична точка зовсім не обов’язково є
точкою екстремуму. Наприклад, функція y = x3 зростає на всій числовій осі. Похідна y′=3x 2 в точці x = 0 дорівнює нулю, тобто y′(0) = 0 , але екстремуму в цій точці немає.
Таким чином, для знаходження екстремумів функції потрібно додатково досліджувати критичні точки. Іншими словами, потрібно знайти достатню умову екстремуму.
Теорема 3 (перша достатня умова екстремуму). Якщо при переході через точку x0 похідна диференційовної функції y = f (x) змінює свій знак з плюса на мінус, то точка x0 є точкою максимуму функції y = f (x) , а якщо з мінуса на плюс, то x0 – точка мінімуму.
Схема дослідження функції y = f (x) на екстремум.
1.Знайти область визначення функції D( f ) .
2.Обчислити похідну y′ = f ′(x) .
3.Знайти критичні точки функції, тобто точки, в яких f ′(x) = 0 або не існує.
4.Дослідити знак похідної зліва і справа від кожної критичної точки і зробити висновок про наявність екстремумів функції.
5.Знайти екстремуми функції, обчисливши значення функції в точках екстремуму.
Приклад 2. Дослідити на екстремум функцію y = 3x−+x22 .
1. Область визначення даної функції D( y) = (−∞;−2) (−2;+∞) .

2.Обчислюємо похідну функції |
y |
′ |
= |
−2x(x + 2) −(3 − x2 ) |
= − |
x2 + 4x +3 |
. |
(x + 2)2 |
(x + 2)2 |
||||||
|
|
|
|
|
|
|
3. Прирівнюємо похідну до нуля і знаходимо критичні точки функції:
y′ = 0 x 2 +4x +3 = 0 x1 = −1, x2 = −3 .
Зауважимо, що в точці x = −2 похідна y′ не існує, але ця точка не є критичною, оскільки вона не
входить в область визначення функції.
4. На числову вісь наносимо область визначення функції і критичні точки (рис.5).
y' |
- |
+ |
+ |
- |
y |
|
-3 |
-2 |
-1 |
|
Рис. 5. |
|
|
|
|
|
Для визначення знаку похідної зліва і справа від критичної точки x = −3 |
виберемо, наприклад, |
|||||
значення x = −4 і x = −2,5 і знайдемо |
y (−4) = −0, 75 < 0 і y (−2,5) = 3 > 0 ; отже, |
y |
|
< 0 при |
x (−∞;−3) і |
|
|
′ |
′ |
|
′ |
|
|
y′ > 0 при x (−3;−2) . |
|
|
|
|
|
|
Аналогічно встановлюємо, що y′ > 0 |
на інтервалі (−2;−1) |
і y′< 0 при x (−1;+∞) . |
|
|||
Згідно з достатньою умовою x = −3 – точка мінімуму даної функції, а x = −1 – точка максимуму. 5. Знаходимо ymin = y(−3) = 3−−3(−+3)2 2 = 6 , ymax = y(−1) = 3−−1(+−1)2 2 = 2 .
Теорема 4 (друга достатня умова екстремуму). Якщо функція y = f (x) двічі диференційовна і
f ′(x0 ) = 0 , а f ′′(x0 ) > 0 , то x0 є точкою мінімуму функції; якщо f ′′(x0 ) < 0 , то x0 є точкою максимуму.
Схема дослідження на екстремум функції y = f (x) за допомогою другої достатньої умови
аналогічна в цілому до наведеної вище схеми. Різниця в п.4, який встановлює наявність екстремуму: тут необхідно знайти другу похідну f ′′(x) і визначити її знак в кожній критичній точці.
Приклад 3. |
Функції, |
що описують залежність загального доходу TR і загальних витрат TC |
|||||
фірми від |
кількості |
одиниць |
Q |
продукції мають вигляд: |
TR(Q) = −0,2Q 2 + 260Q |
(гр.од.) |
і |
TC(Q) = 0,1Q 2 − 40Q +12000 (гр.од.). |
Знайти обсяг Q0 продукції, |
який максимізує прибуток, |
і |
||||
максимальний прибуток. |
|
|
|
|
|
||
Функція прибутку π(Q) є різниця між функцією загального доходу і функцією загальних |
|||||||
витрат, тобто |
|
|
|
|
|
|
|
π(Q) = TR(Q) −TC(Q) = −0,3Q2 +300Q −12000 . |
|
|
|
||||
Значення Q0 , яке максимізує прибуток, є точкою максимуму функції прибутку π(Q) . Знайдемо |
|||||||
критичні точки цієї функції: |
|
– критична точка. |
|
|
|
||
′ |
|
= 0 Q0 =500 |
|
|
|
||
π (Q) = −0,6Q +300 |
|
|
|
||||
|
Оскільки π (Q) = −0,6 < |
0 , то функція π(Q) при Q0 =500 має максимум; |
|
|
|||
|
|
′′ |
|
|
|
|
|
|
πmax (Q) = π(500) = −0,3 500 2 + 300 500 −12000 = 67000 |
(гр.од.). |
|
|
|||
3. Найбільше і найменше значення функції |
|
|
|
||||
Якщо функція |
y = f (x) |
неперервна |
на відрізку [a; b] , то вона досягає на цьому |
відрізку |
|||
найбільшого і найменшого значень. Найбільше і найменше значення функції на відрізку [a; b]
позначають max f (x) та min f (x) і називають глобальним максимумом та глобальним мінімумом
[a;b] [a;b]
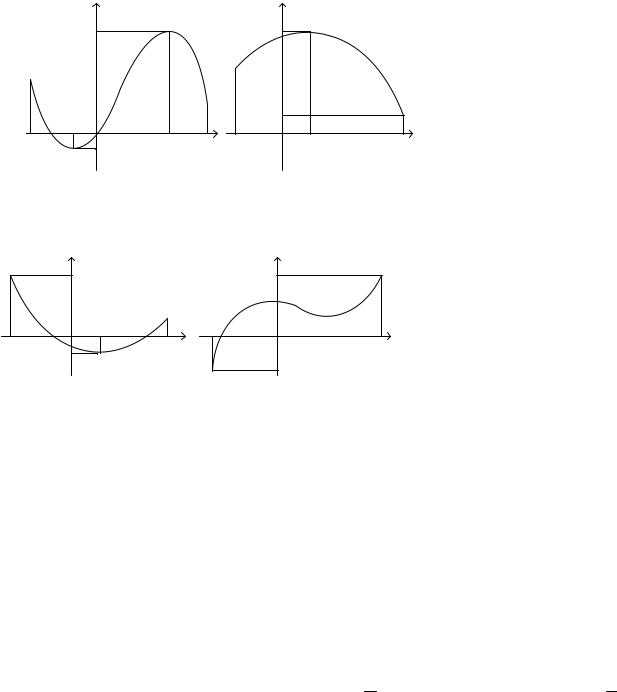
відповідно. Ці значення можуть досягатися у точках локального екстремуму або на кінцях проміжку
(рис. 6).
y |
y |
f(x2) |
f(x1) |
|
|
x1 |
x2 |
f(b) |
|
|
|
|
x1 |
|
||
a |
0 |
b x a |
0 |
b x |
|
|
|
f(x1) |
|
|
|
|
|
|
|
|
|
|
max f (x) = f (x2 ) |
|
|
|
|
|
|
|
[a;b] |
|
|
|
|
max f (x) = f (x1 ) |
|
|
|
|
|
|
|
[a;b] |
|
|
|
|
min f (x) = f (x1) |
|
|
|
min f (x) = f (b) |
||
|
[a;b] |
|
|
|
|
|
[a;b] |
y |
|
|
|
y |
|
|
|
f(a) |
|
|
|
f(b) |
|
|
|
|
|
|
|
|
|
|
|
0 |
x1 |
x |
|
0 |
|
x |
|
a |
b |
a |
|
b |
|
||
f(x1) |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
f(a) |
|
|
max f (x) = f (a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[a;b] |
|
|
|
|
max f (x) = f (b) |
|
|
|
|
|
|
|
[a;b |
] |
|
|
|
min f (x) = f (x1 ) |
|
min f (x) = f (a) |
||||
|
[a;b] |
|
|
|
|
[a;b |
] |
Рис. 6. Найбільше і найменше значення функції на відрізку
Схема відшукання найбільшого і найменшого значень функції y = f (x) на відрізку [a; b] .
1.Знайти похідну f ′(x) .
2.Знайти всі критичні точки на [a; b] , тобто точки, в яких f ′(x) = 0 або не існує.
3.Обчислити значення функції в цих критичних точках та на кінцях відрізка і вибрати з них
найбільше max f ( x) та найменше min f ( x) .
[a;b] [a;b]
Приклад 4. Знайти найбільше і найменше значення функції y = (x − 2)2 e−x на відрізку [0;5] .
1.f ′(x) = 2(x − 2)e−x − (x − 2) 2 e−x = −e−x (x − 2)(x − 4) .
2.f ′(x) = 0 , звідки критичні точки x1 = 2, x2 = 4 (x1, x2 [0;5]) .
3.Значення функції в критичних точках f (2) = 0, f (4) = e44 і на кінцях відрізка f (0) = 4 і f (5) = e95 .
Отже,
max(x −2)2 e−x = f (0)= 4 , |
min(x −2)2 e−x = f (2)= 0 . |
|
|
|
|
[0;5] |
|
[0;5] |
|
|
|
4. Опуклість і вгнутість функції. Точки перегину |
|
|
|
||
Означення 3. Функція y = f (x) |
називається опуклою (опуклою вверх) на інтервалі (a; b) , якщо для |
||||
довільних двох точок |
x1 , x2 з цього проміжку відрізок, |
що |
з’єднує точки |
A(x1 ; f (x1 )) і |
|
B(x2 ; f (x2 )) , розміщений під графіком цієї функції (рис. 7). |
|
|
|
||
Означення 4. Функція y = f (x) |
називається вгнутою (опуклою вниз) на інтервалі (a; b) , якщо для |
||||
довільних двох точок |
x1 , x2 з цього проміжку відрізок, |
що |
з’єднує точки |
A(x1 ; f (x1 )) і |
|
B(x2 ; f (x2 )) , розміщений над графіком цієї функції (рис. 8).
