
- •1. Множини. Дії над множинами
- •2. Множина дійсних чисел та її підмножини
- •3. Поняття функції дійсної змінної
- •3.1. Способи задання функції
- •3.2. Обернена функція
- •3.3. Складена функція
- •4. Елементи поведінки функції
- •4.1. Обмеженість функції
- •4.2. Монотонність функції
- •4.3. Парність, непарність, періодичність
- •5. Елементарні функції
- •6. Числові послідовності
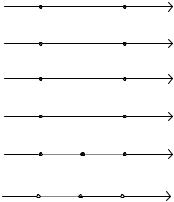
Півінтервали: (a;b] ={x | a < x ≤b} ; [a;b) ={x | a ≤ x <b} .
Інтервал: (a;b) ={x |
| a < x <b} . |
|
|
|
|
||
Поряд |
з |
ними |
розглядаються |
нескінченні |
інтервали |
та |
півінтервали: |
(−∞;a), (b, +∞), (−∞, +∞), (−∞;a], [b; +∞) . Усі вказані множини часто об’єднують терміном проміжок X . Далі будемо мати справу зі спеціальною підмножиною множини дійсних чисел, а саме
ε -околом |
точки |
x0 : |
Uε ( x0 ) ={x |
| x0 −ε < x < x0 +ε} |
(рис. |
3 |
г)). |
Множину |
||||||||
U ε (x0 ) =Uε (x0 ) \ {x0 }називають проколотим ε -околом точки x0 . |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
a) |
|
b |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
b |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
б) |
|
b |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
в) |
|
b |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x0 |
|
|
|
|
|
|
+ε |
|
|
|
|
||
|
|
|
-ε |
|
x0 |
x0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
г) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x0 |
|
|
x |
|
|
+ε |
|
|
|
|
|||
|
|
|
-ε |
|
0 |
x0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
д) |
|
|
|
|
|
|
|
||
|
|
|
Рис. 3. Підмножини множини |
: |
|
|
|
|||||||||
|
|
|
а) відрізок; б) півінтервали; в) інтервал; |
|
|
|
||||||||||
|
|
|
г) ε -окіл; |
д) проколотий ε -окіл |
|
|
|
|||||||||
Звернемо увагу, що відрізок [a;b] і інтервал (a;b) на перший погляд відрізняються дуже мало:
перша підмножина “багатша” за другу всього на дві точки – кінці відрізка. Однак така різниця є дуже принциповою і надзвичайно важливою в математиці. Справа в тому, що будь-яка точка інтервалу
(a;b) є внутрішньою точкою, тобто і лівіше, і правіше від цієї точки знаходяться інші точки інтервалу.
3. Поняття функції дійсної змінної
Сталою називається величина, яка зберігає одне і те ж значення. Наприклад, відношення довжини кола до його діаметру є величина стала і дорівнює π .
Змінною величиною називається величина, яка може набувати різних числових значень.
Наприклад, |
якщо |
тіло рухається рівномірно, |
то s =vt , де шлях s і |
час |
t – змінні величини, |
швидкість v |
– стала величина. |
|
|
|
|
Означення 6. Якщо кожному елементу x X |
ставиться у відповідність певний єдиний елемент |
||||
y Y , то говорять, що на множині X задана функція y = f (x) . |
|
|
|||
При цьому x |
називають незалежною змінною (або аргументом), а |
y |
– залежною змінною. |
||
Символ f означає закон відповідності між x і y . |
|
|
|||
Множину |
X |
називають областю визначення функції і позначають |
D( f ) , а множину Y – |
||
областю значень функції (позначатимемо її E( f ) ). Якщо множина D( f ) спеціально не описана, то вона визначається як множина тих значень x , для яких y = f (x) має зміст.
Зауваження. Функція, задана згідно з означенням 6, називається однозначною. Якщо у цьому
означенні |
відкинути умову єдиності елемента y E( f ) , то |
прийдемо |
до більш загального |
поняття – |
так званої багатозначної функції, яка допускає, щоб кожному значенню x D( f ) |
||
відповідало не одне, а декілька (можливо, безліч) значень |
y E( f ) . |
Надалі, говорячи про |
|
функцію, матимемо на увазі лише однозначну функцію. |
|
|
|

Приклад 3. Знайти область визначення функції
y = |
4 − x2 |
+log2 (x +1). |
|
|
|
x |
|
|
|||
|
|
|
|
|
|
Областю визначення даної функції є всі значення x , які задовольняють умови: |
|||||
4 − x2 ≥ 0 |
(x −2)(x + 2) ≤ 0 |
|
|
||
|
≠ 0 |
|
. |
|
|
x |
x ≠ 0 |
|
|||
|
+1 > 0 |
|
|
|
|
x |
x > −1 |
|
|
||
|
|
|
|
|
|
Отже, область визначення заданої функції x (−1;0) (0;2] . |
|||||
Областю визначення функції може бути вся числова вісь |
або перераховані вище підмножини |
||||
числової осі чи їх об’єднання. У наступній лекції детально познайомимось зі спеціальним класом функцій, область визначення яких – множина натуральних чисел . Такі функції називаються
числовими послідовностями.
3.1. Способи задання функції
Аналітичний спосіб. Найбільш поширеним є аналітичний спосіб, тобто задання функції за
допомогою формули. Розглянемо деякі різновиди аналітичного способу задання функції. |
|
|
|||||||||||||||||||
а) |
Якщо залежність між x і y |
задана у вигляді |
y = f (x) , то кажуть, |
що функція f |
задана явно. |
||||||||||||||||
Наприклад, |
y =3x + 2 , y = x2 +sin x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
б) Якщо змінні |
x |
і |
y пов’язані між собою рівнянням вигляду |
F(x, y) =0 , тобто не розв’язаним |
|||||||||||||||||
відносно y або x , то кажуть, що функція y = f (x) задана неявно. Наприклад, |
tg (x + y) − x − y = 0 . |
||||||||||||||||||||
Інколи рівняння |
F(x, y) =0 можна розв'язати |
щодо |
x |
або |
y |
|
і |
звести до функції, заданої |
|||||||||||||
аналітично: |
y = f (x) |
або x = g( y) . Наприклад, |
рівність |
x2 |
+ y 2 |
− 4 = 0 , що задає коло радіуса 2 |
з |
||||||||||||||
центром в початку координат, неявно визначає такі функції: |
y = |
4 − x2 , −2 ≤ x ≤ 2 (верхнє півколо) і |
|||||||||||||||||||
y = − |
4 − x2 , −2 ≤ x ≤ 2 |
(нижнє |
півколо) |
або |
x = |
4 − y2 , −2 ≤ y ≤ 2 |
(праве |
півколо) |
і |
||||||||||||
x = − |
4 − y2 , −2 ≤ y ≤ 2 |
(ліве півколо). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
в) |
Якщо |
x і y |
задаються як функції допоміжної змінної – параметра t , |
то кажуть, що функція |
|||||||||||||||||
задана параметрично. Наприклад, параметричне рівняння еліпса |
x2 |
|
+ |
|
y |
2 |
=1 має вигляд |
|
|||||||||||||
a2 |
|
b |
2 |
|
|||||||||||||||||
|
x = a cos t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
, t [0; 2π] . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
=bsin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) Функція може бути задана на окремих підмножинах різними аналітичними виразами. Зокрема,
для випадку двох підмножин |
|
|
|
|||
f |
1 |
(x), |
x D( f |
1 |
) |
. |
y = f (x) = |
|
|
|
|||
f2 (x), |
x D( f2 ) |
|
||||
Тут областю визначення функції f (x) буде D( f ) = D( f1 ) D( f 2 ) , причому D( f1 ) ∩ D( f 2 ) = .
Табличний спосіб. Важливим способом задання функції є табличний, коли значення x та відповідні їм значення y задаються у вигляді таблиці:
x |
x1 |
x2 |
… |
xi |
xi+1 |
… |
xn |
y |
y1 |
y2 |
… |
yi |
yi+1 |
… |
yn |
Табличний спосіб задання функції часто використовується в економіці, коли інформація про незалежну змінну та функцію подається у вигляді зліченної кількості точок. Якщо Вас цікавить значення функції всередині проміжка [xi , xi+1 ] , то можна застосувати один із багатьох способів
інтерполяції. Наприклад, якщо застосувати лінійну інтерполяцію, то для кожного x [xi , xi+1 ]
