
lectures / Kospekt_Ch2
.pdf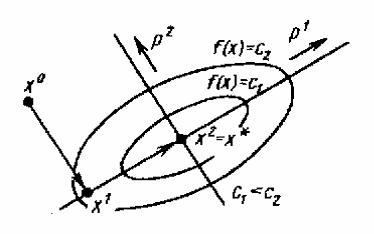
Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”
5.8.Метод спряжених напрямків (метод Пауела)
Всі описані вище прямі методи мінімізації вимагають нескінечного числа ітерації для точного визначення точки оптимуму цільової функції. Це відноситься і до дуже випуклих квадратичних функцій, питання мінімізації, які добре вивчені.
Однак існують прямі ітераційні методи, які призводять до точки оптимуму (мінімуму) дуже випуклої квадратичної функції за скінченне число кроків. Як вже відзначалось, від таких методів розумно очікувати високої ефективності і в випадку випуклої не квадратичної цільової функції. Опишемо один з них.
|
Рис. 5.20. Графічна інтерпретація ідеї методу Пауела |
|||
Нехай |
p1 і p2 – |
напрями головних осей цих еліпсів (рис.5.20, вони |
||
можуть бути знайдені як ортонормований базис із власних векторів матриці A |
||||
квадратичної |
функції). |
Якщо |
з довільної точки x0 E 2 |
виконати ітераційну |
процедуру xk |
x k pk , |
k = l, |
2, де величина кроку k |
знаходиться із умов |
вичерпного спуску, то, очевидно, потрібно не більше двох кроків для пошуку точки х*.
71
Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації” |
|
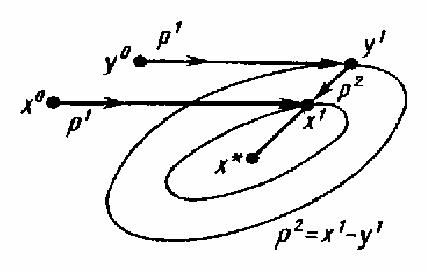
Виберемо деякий напрям p1 та дві точки x0 і y0 такі, щоби вектори x0 |
– |
y0 і p1 були неколінеарні. Виконавши вичерпний спуск з точок x0 і y0 |
в |
напрямі p1 , отримаємо точки x1 і y1 . По властивості вичерпного спуску в точках x1 і y1 . має місце дотику відповідних прямих (напрямів зниження) і еліпсів
(ліній рівня цільової функції).
Так як еліпси відрізняються гомотетією з центром в точці х*, то точки х*, x1 і y1 розміщені на одній прямій. Тому, припустимо p2 x1 y1 і розв’язуючи задачу f (x1 αp2 ) min , ми знаходимо точку х*. Таким чином, і в цьому випадку розв’язання задачі мінімізації квадратичної дуже випуклої функції буде отримано за скінчене число кроків.
Рис. 5.21. Особливості реалізації методу Пауела
Крок 1. Вибрати початкову точку x0 E 2 .
Крок 2. Припустимо p1 |
e1 . |
Знайти точку x1 за допомогою вичерпного |
||
спуску з точки x |
0 |
за напрямом |
p : |
f (x1 ) = min f (x0 + αp1 ) . |
|
|
1 |
α R |
|
|
|
|
|
|
Крок 3.
а) припустимо y x c ;
72

Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”
б) знайти точку у з умови вичерпного спуску з точки y0 за напрямом p1 :
f (y1 ) = min f (y0 + αp1 ) ,
α R
в) припустимо p |
2 |
x |
y , знайти точку |
x |
2 |
з умови f (x2 )= min f (x0 |
+ αp2 ) . |
|
1 |
1 |
|
α R |
|
||
|
|
|
|
|
|
|
Крок 4. Розрахунки завершити, припустити х*=x2 .
Пошук точки мінімуму проводиться за так званими спряженими напрямами.
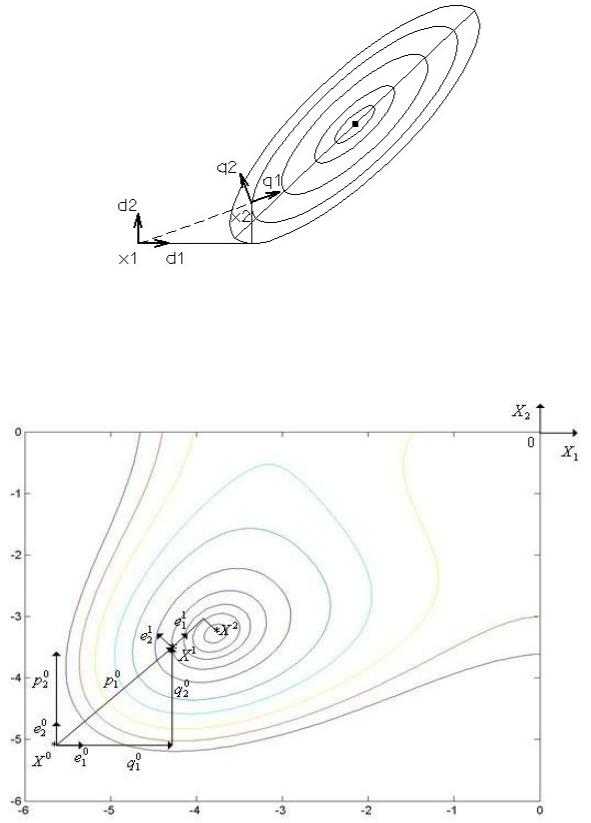
Рис.5.22. Схема реалізації методу Пауела Наведемо приклад реалізації методу спряжених градієнтів
73

Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”
Інший приклад застосування методу спряжених напрямків зображено на рис.5.23.
Рис.5.23. Приклад розв’язання оптимізаційної задачі з використанням методу спряжених напрямків
1.Метод спряжених напрямків найчастіше використовується для розв’язання оптимізаційних задач у порівнянні з іншими методами нульового порядку;
2.В процесі практичного застосування необхідно доповнити алгоритм процедурами перевірки сходимості та лінійної незалежності системи напрямів;
3.Якщо ЦФ квадратична та містить мінімум, то точка мінімуму знаходиться за n кроків, де n – число змінних ЦФ. В іншому випадку за більшу кількість кроків.
5.9.Метод Розенброка
При розв’язанні задачі методом Розенброка (метод обертових координат)
використовується перетворення на кожній ітерації системи координат таким чином, щоб у новій системі координат одна з осей співпадала з напрямком
74
Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”
попереднього кроку. Інші осі нової системи координат звичайно знаходять за допомогою процедури ортогоналізації Грамма-Шмидта.
Рис.5.24. Ідея методу Розенброка
Траєкторія пошуку мінімуму функції Хімельблау методом Розенброка
(рис.5.25). min f (x, y)= λ(x2 + y 11)2 + (x + y2 7)2 .
Рис.5.25
75
Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”
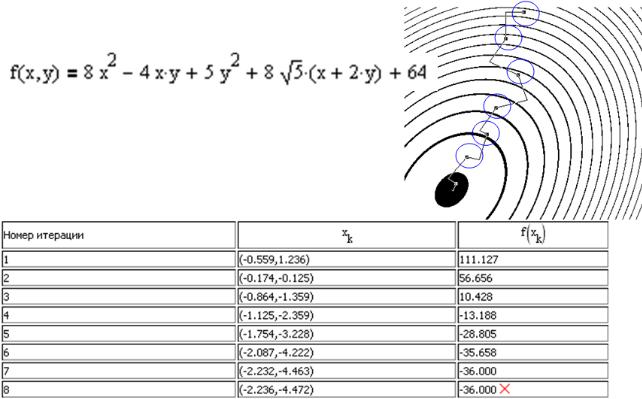
Інший приклад застосування методу Розенброка зображено на рис.5.26.
Рис.5.26. Результат розв’язання задачі
У порівнянні з методом Хука-Дживса метод Розенброка володіє, як правило, більш високою ефективністю для функцій у формі ярів з не прямолінійною формою ярів та впадин.
На відміну від інших методів нульового порядку алгоритм Розенброка орієнтований на відшукання оптимальної точки в кожному напрямку, а не просто на фіксоване зрушення в усіх напрямках. Величина кроку в процесі пошуку безупинно змінюється в залежності від рельєфу поверхні рівня.
Сполучення обертання координат з регулюванням кроку робить метод Розенброка ефективним при розв’язання складних задач оптимізації.
На завершення опису методів нульового порядку наведемо результати розв’язання оптимізаційної задачі з використанням усів вищерозглянутих методів в залежності від точності отриманих результатів. Під ефективністю будемо розуміти кількість обчислень значень цільової функції. З отриманих даних слідує, що найбільш ефективним є метод Розенброка. Трохи гіршими
76
Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”
параметрами ефективності, в області високих точностей, володіє метод Пауела,
хоча при менших точностях метод Пауела є ефективніший навіть за метод Розенброка. Досить хорошим значенням ефективності володіє метод Хука-
Дживса та метод координатного спуску.
Слід зауважити, що отримані результати дещо змінюються в залежності від початкової точки та виду цільової функції.
Результати порівняння ефективності методів нульового порядку Таблиця 5.2
Метод |
Метод по |
Метод |
Метод |
Метод |
Метод |
|
координатного |
Нелдера- |
Хука- |
Пауелла |
Розенброка |
Точність |
|||||
|
спуску |
Міда |
Дживса |
|
|
|
|
|
|
|
|
0.1 |
4 |
15 |
6 |
2 |
3 |
|
|
|
|
|
|
0.01 |
5 |
19 |
8 |
2 |
5 |
|
|
|
|
|
|
0.001 |
6 |
24 |
10 |
2 |
6 |
|
|
|
|
|
|
0.0001 |
7 |
27 |
12 |
4 |
8 |
|
|
|
|
|
|
0.00001 |
8 |
30 |
!!! |
249 |
9 |
|
|
|
|
|
|
5.10. Контрольні запитання та завдання для самостійного розв’язання
22.Яка оптимізаційна задача називається задачею безумовної оптимізації?
23.Яка ідея методу пошуку по симплексу?
24.Яка перевага методу пошуку по симплексу?
25.Які недоліки методу пошуку по симплексу?
26.Які основні кроки включає алгоритм пошуку оптимуму з використанням методу пошуку по симплексу?
27.Яка ідея методу Нелдера-Міда?
28.Яка перевага методу Нелдера-Міда?
29.Які недоліки методу Нелдера-Міда?
30.Які основні кроки включає алгоритм пошуку оптимуму з використанням методу Нелдера-Міда?
31.Яка ідея методу Хука-Дживса?
32.Яка перевага методу Хука-Дживса?
77
Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”
33.Які недоліки методу Хука-Дживса?
34.Які основні кроки включає алгоритм пошуку оптимуму з використанням методу Хука-Дживса?
35.Яка ідея методу Пауела?
36.Яка перевага методу Пауела?
37.Які недоліки методу Пауела?
38.Які основні кроки включає алгоритм пошуку оптимуму з використанням методу Пауела?
39.Яка ідея методу Розенброка?
40.Яка перевага методу Розенброка?
41.Які недоліки методу Розенброка?
42.Які основні кроки включає алгоритм пошуку оптимуму з використанням методу Розенброка?
22. Розв’язування задачі багатопараметричної оптимізації методами прямого пошуку
№ |
|
|
Функція |
|
Метод розв’язку |
|
п.п. |
|
|
|
|||
|
|
|
|
|
|
|
1. |
x2 xy 3y2 12x 15y 2 |
|
Знайти мінімум за допомогою |
|||
|
|
|
|
|
|
симплекс-методу |
2. |
x2 2xy 5y2 12x 15y |
|
Знайти максимум методом |
|||
|
|
|
|
|
|
Нелдера-Міда |
3. |
x2 4xy 2y2 |
6x 8y |
|
Знайти мінімум методом |
||
|
|
|
|
|
|
Хука-Джівса |
4. |
x2 xy 3y2 |
12x 11y 6 |
|
Знайти максимум за |
||
|
|
|
|
|
|
допомогою симплекс-методу |
5. |
x2 2xy y2 3x 14y |
|
Знайти мінімум методом |
|||
|
|
|
|
|
|
Нелдера-Міда |
6. |
3x2 2xy 4y 2 |
3x 2y 5 |
|
Знайти мінімум методом |
||
|
|
|
|
|
|
Хука-Джівса |
7. |
3x2 2xy 2y2 2x 10y |
|
Знайти мінімум за допомогою |
|||
|
|
|
|
|
|
симплекс-методу |
8. |
2x2 |
2xy 2y2 |
12x 12y 3 |
|
Знайти максимум методом |
|
|
|
|
|
|
|
Хука-Джівса |
9. |
2x2 |
5xy 2y2 |
20x 15y 2 |
|
Знайти максимум за |
|
|
|
|
|
|
|
допомогою симплекс-методу |
10. |
x2 xy 2y2 5x 10y 10 |
|
Знайти мінімум методом |
|||
|
|
|
|
|
|
Нелдера-Міда |
|
|
|
|
|
78 |
|
Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”
№ |
|
|
|
Функція |
Метод розв’язку |
п.п. |
|
|
|
||
|
|
|
|
|
|
11. |
x2 4y2 xy 6x 4y 2 |
Знайти мінімум за допомогою |
|||
|
|
|
|
|
симплекс-методу |
12. |
4x2 |
2xy y2 |
16x 10y 2 |
Знайти максимум методом |
|
|
|
|
|
|
Хука-Джівса |
13. |
2x2 |
5xy 4y2 3x 5y 6 |
Знайти максимум за |
||
|
|
|
|
|
допомогою симплекс-методу |
14. |
4x2 2xy 2y2 |
12x 2y 4 |
Знайти мінімум методом |
||
|
|
|
|
|
Нелдера-Міда |
15. |
2x2 2y2 xy 16x 10y 2 |
Знайти мінімум за допомогою |
|||
|
|
|
|
|
симплекс-методу |
16. |
2x2 |
xy y2 |
12x y6 5 |
Знайти максимум методом |
|
|
|
|
|
|
Хука-Джівса |
17. |
2x2 |
xy 4y2 |
20x 12y 4 |
Знайти максимум за |
|
|
|
|
|
|
допомогою симплекс-методу |
18. |
x2 xy 3y2 12x 14y 6 |
Знайти мінімум методом |
|||
|
|
|
|
|
Нелдера-Міда |
19. |
x2 2xy 4y2 |
3x 6y 8 |
Знайти мінімум за допомогою |
||
|
|
|
|
|
симплекс-методу |
20. |
x2 xy 3y2 |
10x 14y 2 |
Знайти максимум методом |
||
|
|
|
|
|
Хука-Джівса |
21. |
4x2 xy 5y2 |
50x 60y 5 |
Знайти мінімум за допомогою |
||
|
|
|
|
|
симплекс-методу |
22. |
3x2 3xy 2y2 |
10x 8y 5 |
Знайти мінімум методом |
||
|
|
|
|
|
Хука-Джівса |
23. |
8x2 |
4xy 6y2 16x 10y 2 |
Знайти максимум за |
||
|
|
|
|
|
допомогою симплекс-методу |
24. |
5x2 xy y2 10x y 5 |
Знайти мінімум методом |
|||
|
|
|
|
|
Нелдера-Міда |
25. |
4x2 |
4xy 2y2 2x 10y 8 |
Знайти максимум методом |
||
|
|
|
|
|
Хука-Джівса |
26. |
x2 3xy y2 10x 12y 6 |
Знайти мінімум за допомогою |
|||
|
|
|
|
|
симплекс-методу |
27. |
2x2 |
xy 5y2 |
4x 5y 6 |
Знайти максимум методом |
|
|
|
|
|
|
Нелдера-Міда |
28. |
5x2 3xy y2 |
3x 4y |
Знайти мінімум методом |
||
|
|
|
|
|
Хука-Джівса |
29. |
x2 3xy 2y2 |
x 5y 3 |
Знайти максимум за |
||
|
|
|
|
|
допомогою симплекс-методу |
30. |
5x2 3xy 4 y2 |
5x y 4 |
Знайти мінімум методом |
||
|
|
|
|
|
Нелдера-Міда |
79
Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”
Література
1.Таха Х. Введение в исследование операций: В 2-х кн. Кн. 1. Пер. с англ.
-М.: Мир, 1985. - 479 с.
2.Таха Х. Введение в исследование операций: В 2-х кн. Кн. 2. Пер. с англ.
-М.: Мир, 1985. - 496 с.
3.Теслюк В.М., Андрійчук М.І. Конспект лекцій з курсу «Методи синтезу та оптимізації» для студентів базового напряму «Комп’ютерні науки», Ч.1. -
Львів, 2005 – 64 с.
4.Теслюк В.М., Загарюк Р.В. Методи багатокритеріальної оптимізації: Ч.1. Конспект лекцій з курсу ―Методи багатокритеріальної оптимізації‖ для студентів спеціальності 8.05010103 ―Системне проектування‖. – Львів: Видавництво Львівської політехніки, 2012. – 52 с.
5.Mykola Medykovskyy, Vasyl Teslyuk, Oleh Shunevych The Gomory method applying for wind farm structure determination // Proc. of the VI-th Intern. Conf. of Computer Science & Information Technologies 2011 (CSIT’2011). – Lviv – P. 290 - 291.
6.Halych K.V., Tesluyk V.M. Development of system for automation of optimal menu forming in preschool educational institutions // Proc. of the III-d Intern. Conf. of Computer Science & Engineering, (CSE’2011). – Lviv – P. 70 – 71.
7.Теслюк В.М., Зелінський А.Я., Хамза Алі Юсеф Аль Шавабкех, Застосування методу гілок та границь для зменшення потужності множини альтернативних рішень при розв’язанні задач синтезу МЕМС // Моделювання та інформаційні технології. Зб. наук. пр. ІППМЕ ім.Г.Є.Пухова НАН України. –
Київ, 2009, Вип. 50. – С.157 - 165.
8.Схрейвер А. Теория линейного и целочисленного программирования: в 2-х томах.; перевод с английского. 1991г. 360с.
9.Ху Т. Целочисленное программирование и потоки в сетях.; перевод с английского. 1974г.
10.Кузнецов А.В., Сакович В.А., Холод Н.И. Высшая математика: Математическое программирование. Ученик - 2-е издание. 2001г. 351с.
11.Карманов В.Г. Математическое программирование: Учебное пособие – 5-е издание, стереотип-М:ФИЗМАТ, 2001г.-264с.
12.Белоусов Е.Г. Введение в выпуклый анализ и целочисленное программирование. М.:Издательство МГУ, 1977г.
13.Федосеев В.В., Гармаш А.Н., Дайитбегов Д.М.: Экономикоматематические методы и прикладные модели: Учеб.пособие для вузов/ЮНИТИ, 1999г.-391с.
14.Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н.; под ред. Проф.Н.Ш.Кремера. : Исследование операций в экономике; учеб. Пособие для вузов.
15.Реклейтис Г., Рейвиндрон А., Рзгсдед К. Оптимизация в технике: В 2-х кн. Кн. 1. Пер. с англ. - М.: Мир, 1986. - 349 с.
16.Реклейтис Г., Рейвиндрон А., Рзгсдел К. Оптимизация в технике: В 2-х
кн. Кн.2. Пер. с англ. - М.: Мир, 1986. - 320 с.
80
