lectures / Kospekt_Ch2

Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”

Метод Гоморі у порівнянні з методом гілок та границь потребує набагато

менший обсяг обчислень.

4.6.Контрольні запитання та завдання для самостійного розв’язання

1.Яка оптимізаційна задача називається задачею цілочисельного програмування?

2.Яка задача називається задачею цілочисельного лінійного програмування?

3.Які методи для розв’язання задач цілочисельного програмування Ви знаєте?

4.Які значення приймають проектні параметри в ЗЦП?

5.Яка перевага розв’язання ЗЦП з використанням методу перебору варіантів рішень?

6.Які недоліки розв’язання ЗЦП з використанням методу перебору варіантів рішень?

7.Які основні кроки включає алгоритм розв’язання ЗЦП з використанням методу перебору варіантів рішень?

8.Яка перевага розв’язання ЗЦП з використанням графічного методу?

9.Які недоліки розв’язання ЗЦП з використанням графічного методу?

10.Які основні кроки включає алгоритм розв’язання ЗЦП з використанням графічного методу?

11.Яка перевага розв’язання ЗЦП з використанням методу гілок та границь?

12.Які недоліки розв’язання ЗЦП з використанням методу гілок та границь?

13.Які основні кроки включає алгоритм розв’язання ЗЦП з використанням методу гілок та границь?

14.Яка перевага розв’язання ЗЦП з використанням методу Гоморі?

15.Які недоліки розв’язання ЗЦП з використанням методу Гоморі?

16.Які основні кроки включає алгоритм розв’язання ЗЦП з використанням методу Гоморі?

41

Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”

17.Який з вищеперерахованих методів найефективніший?

18.На заводі виконують зборку двох видів приладів, які використовують три види мікросхем А, В і С. На виготовлення першого приладу використовується одна мікросхема А, дві мікросхеми В і одна мікросхема С. Для другого приладу витрати мікросхем, відповідно, рівні 4, 2, 3. Запас мікросхем А, В і С - 65, 30 і 40 шт. Скільки приладів кожного типу потрібно зібрати для отримання максимального прибутку, якщо ціна першого приладу складає 15 у.о., а другого - 20 у.о.?

19.На придбання обладнання для нової виробничої дільниці є капіталовкладення в розмірі 45 тис. у.о,, а для його розміщення виділена площа в 75 м2. Можна придбати обладнання трьох видів. Одиниця обладнання першого вигляду займає 9 м2 і вартує 6 тис. у.о. Для обладнання 2-го І 3-го видів ці дані такі: 4 м2 і 3 тис. у.о., 3 м2 і 1.5 тис. у.о. Прибуток від одиниці нового обладнання кожного виду становить 4.5, 2 і 1 тис. у.о., відповідно. Скільки треба придбати нового обладнання кожного виду, щоб отримати найбільший прибуток і, при цьому, повністю витратити виділені капіталовкладення?

20.Редакційно-видавничий відділ (РВВ) в даному місяці має ліміт на папір 850 кг, а підготовлені до видання посібники а, b, с вимагають витрат відповідно 50, 70 і 80 кг на 100 примірників. Трудомісткість виготовлення 100

примірників рівна 80, 60 і 90 нормо-год, а місячний трудовий ресурс РВВ становить 940 нормо-год. Ціна одного посібника а, b, с 0,9, 1 і 2 у.о. відповідно.

Знайти місячний план випуску літератури, максимізуючий її сумарну вартість при умові повного використання трудового ресурсу РВВ?

21.Для озеленення периметра площі, довжина якого рівна 120 м, можуть бути використані жоржини, бегонії і айстри. На один погонний метр може бути висаджено або 3 кущі жоржин, або 5 бульб бегонії, або 10 кущів айстр. Вартість куща жоржин 2 у.о., бульби бегонії 1 у.о., куща айстр 0,2 у.о. В наявності є 60

кущів жоржин, 280 бульб бегоній і 500 кущів айстр. Знайти такі кількості рослин кожного виду для забезпечення озеленення з найменшою сумарною вартістю квітів?

42

Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”

РОЗДІЛ 5. МЕТОДИ РОЗВ’ЯЗАННЯ ЗАДАЧ БЕЗУМОВНОЇ ОПТИМІЗАЦІЇ З ВИКОРИСТАННЯМ МЕТОДІВ НУЛЬОВОГО ПОРЯДКУ

5.1 Поняття багатопараметричної оптимізації

Переважна більшість реальних задач оптимізації, які представляють практичний інтерес, є багатовимірними: в них цільова функція залежить від декількох аргументів (проектних параметрів), причому, іноді їх число може бути надзвичайно великим, десятки, сотні і навіть тисячі.

Математична постановка таких задач аналогічна їх постановці в одновимірному випадку, а саме: необхідно знайти такі значення проектних параметрів, які забезпечують найменше (найбільше) значення цільової функції,

забезпечуючи виконання заданих обмежень на проектні параметри.

Як і в одновимірному випадку, характер задачі і, відповідно, можливі методи її розв’язання істотно залежать від тієї інформації про цільову функцію,

яка нам доступна в процесі дослідження. В одних випадках цільова функція задається аналітичною формулою, будучи при цьому диференційованою функцією. Тоді можна обчислити її похідні, отримати явний вираз для градієнта функції, який можна визначити в кожній точці області визначення та отримати напрям максимального зростання чи спадання функції, і використати цю інформацію для розв’язання поставленої задачі багатовимірної оптимізації.

Вінших випадках ніякої формули чи виразу для цільової функції немає, а

єлише можливість визначити її значення в будь-якій точці області визначення,

шляхом проведення експериментів. В таких задачах в процесі розв’язання задачі ми фактично можемо знайти значення цільової функції лише в певному числі точок, і по цій інформації необхідно наближено встановити її найменше значення для всієї області, що досить часто зустрічається на практиці.

Багатовимірні задачі, природно, є більш складними і трудомісткими, ніж одновимірні, причому, труднощі при їх розв’язанні зростають при збільшенні

43

Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”

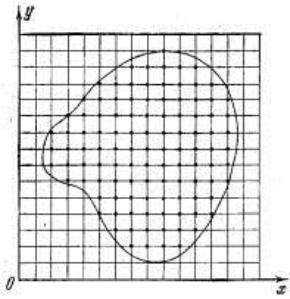
розмірності. Для того, щоб краще відчути це, візьмемо найпростіший по своїй ідеї наближений метод пошуку найменшого значення функції, який обговорювався для одновимірних задач оптимізації (метод загального перебору). Покриємо область, що розглядається сіткою з кроком h (Рис. 5.1) і

визначимо значення цільової функції в її вузлах. Порівнюючи отримані числа між собою, знайдемо серед них найменше і приймемо його за найменше значення цільової функції для всієї області.

Рис. 5.1. Побудова сітки з кроком h і вибір "пробних" точок у вузлах сітки для наближеного визначення найменшого значення цільової функції двох змінних

Як ми вже обговорювали вище, цей метод використовується для розв’язання одновимірних задач оптимізації. Іноді він застосовується також для розв’язання двовимірних, рідше тривимірних задач. Однак для задач більшої розмірності він практично непридатний через величезні затрати ресурсів ПК,

які необхідні для проведення обчислень в процесі розв’язання оптимізаційної задачі.

Припустимо, що цільова функція залежить від п'яти змінних, а область визначення є п’ятивимірним кубом, кожну сторону якого при побудові сітки ми поділимо на 40 частин. Тоді загальна кількість вузлів сітки буде дорівнювати

44

Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”

108. Нехай обчислення значення функції в одній точці вимагає 1000

арифметичних операцій. У такому випадку, загальне число операцій становитиме 1011. Якщо в нашому розпорядженні є ПК з швидкодією 1 млн.

операцій в секунду, то для розв’язання оптимізаційної задачі за допомогою даного методу буде потрібно 105 секунд, що перевищує добу безперервної роботи. Додавання ще однієї незалежної змінної збільшить цей час в 40 разів.

Проведена оцінка показує, що для великих задач оптимізації метод суцільного перебору непридатний. Іноді суцільний перебір замінюють випадковим пошуком. В цьому разі точки сітки переглядаються не підряд, а у випадковому порядку. В результаті, пошук найменшого значення цільової функції істотно прискорюється, але втрачає свою надійність.

5.2 Класифікація методів нелінійного програмування

Загальним для методів нелінійного програмування є те, що їх використовують при розв’язанні оптимізаційних задач з нелінійними критеріями оптимальності та обмеженнями. Суть їх - у визначенні набору незалежних змінних (проектних параметрів), що дають найбільший чи найменший (оптимальний) приріст функції. Дана група методів застосовується як для детермінованих, так і стохастичних процесів.

Методи розв’язання задач нелінійного програмування (поділяють на

задачі умовної та безумовної оптимізації.

Взадачах безумовної оптимізації відсутні обмеження на проектні параметри, а задачі умовної оптимізації включають обмеження на проектні параметри.

Всвою чергу методи розв’язання задач безумовної оптимізації можна розділити на чотири підгрупи, а саме: методи нульового порядку, методи першого та другого порядків і квазінютоновські методи.

45

Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”

Методи нульового порядку (МНП) призначені для розв’язання задач безумовної оптимізації і використовують в процесі розв’язання оптимізаційної задачі лише значення цільової функції.

Методи першого порядку (МПП), на відміну від методів нульового порядку, використовують значення перших похідних від цільового функції і значення ЦФ.

Методи другого порядку (МДП) під час розв’язання задач безумовної оптимізації використовують значення цільової функції та перші і другі похідні від ЦФ.

Квазінютонівські методи (КМ), на відміну від методів другого порядку,

де використовуються другі похідні від ЦФ, в процесі розв’язання оптимізаційної задачі використовують апроксимацію других похідних від ЦФ використовуючи для цієї процедури перші похідні від ЦФ.

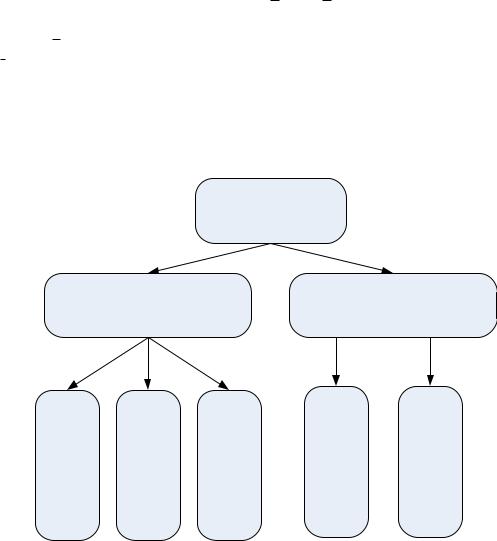
Методи безумовної оптимізації

Рис.5.2. Класифікація методів для розв’язання задач безумовної оптимізації

5.3. Особливості методів прямого пошуку

Отже, прямі методи (методи нульового порядку) не потребують інформації про цільову функцію в явному виді. В даному випадку мається на

46

Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”

увазі явний вираз для цільової функції. Вони не потребують регулярності і неперервності цільової функції та існування першої та другої похідних. Це є суттєвою перевагою при розв’язанні складних технічних і економічних задач.

При реалізації прямих методів суттєво скорочується етап підготовки до розв’язання задачі, так як немає необхідності в визначенні перших та других похідних. Прямі методи в основному носять евристичний характер. До прямих методів відноситься цілий ряд алгоритмів, які відрізняються за своєю ефективністю. Ці методи призначені для рішення задач безумовної оптимізації

(визначити мінімум цільової функції f (x) , де x належить області E n

f (x)

.

де E n - n - вимірна область рішень оптимізаційної задачі.

Методи прямого пошуку

Рис.5.3. Класифікація методів прямого пошуку

47

Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”

5.4. Метод пошуку по симплексу ( S 2 - метод)

Перші спроби розв’язання оптимізаційних задач без обмежень з використанням прямого пошуку пов'язані з використанням одновимірних методів оптимізації. Як правило, при реалізації таких методів область визначення показника якості функціонування системи (цільової функції)

міняється на дискретну множину (сіткою) точок простору керованих змінних, а

потім використовуються різні стратегії зменшення області, яка містить розв’язання задачі. Часто ця процедура виявляється еквівалентною рівномірному пошуку у вузлах сітки і, отже, непридатна для розв’язання задач з числом змінних більше від 2. Більш корисна ідея полягає у виборі базової точки і оцінці значень цільової функції в точках, які оточують базову точку.

Наприклад, при розв’язання задачі з двома змінними можна скористатися квадратним зразком, зображеним на рис. 5.4. Потім «найкраща» з п'яти точок,

які досліджують вибирається як наступна базова точка, навколо якої будується аналогічний зразок (рис.5.5). Якщо ні одна з кутових точок не має переваги перед базовою, то розміри зразка потрібно зменшити, після чого продовжити пошук. Завершується процес пошуку оптимуму, коли різниця між вузлами зразка не стане менше деякої наперед заданої величини.

Цей тип еволюційної оптимізації був використаний Боксом та іншими дослідниками для аналізу функціонування промислових підприємств, коли ефект варіювання значень змінних, які описують виробничі процеси,

вимірюється з помилкою. В задачах великої розмірності обчислення значень цільової функції проводиться в усіх вершинах, а також в центрі ваги гіперкуба,

тобто в точках так званого кубічного зразка. Якщо кількість змінних

(розмірність простору в якому ведеться пошук) рівна n , то пошук за кубічним зразком вимагає 2n 1 обчислень значень функції для одного зразка. При збільшенні розмірності задачі необхідна кількість обчислень значення цільової функції зростає надзвичайно швидко. Таким чином, незважаючи на логічну простоту пошуку за кубічним зразком, виникає необхідність використання

48

Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”

більш ефективних методів прямого пошуку для розв’язання практичних оптимізаційних задач.

Схема пошуку оптимуму оптимізаційної задачі для двовимірної області зображена на рис.5.5.

Рис. 5.4 Квадратний зразок

Рис.5.5. Схема пошуку оптимуму за квадратним взірцем

5.5. Метод пошуку оптимуму по симплексу

Одна із стратегій методу пошуку по симплексу, яка викликає особливий інтерес у дослідників (пошук по симплексу), запропонована Спендлі, Хекстом і Хімсвортом. Слід відмітити, що вказаний метод та інші подібні методи не мають відношення до симплекс-методу розв’язання задач лінійного програмування, а схожість назв носить випадковий характер. Процедура

49

Конспект лекцій Ч.2. Теслюк В.М., Пелешко Д.Д. Методи синтезу та оптимізації”

симплексного пошуку Спендлі, Хекста і Хімсворта грунтується на тому, що експериментальним зразком, який містить найменшу кількість точок, є

регулярний симплекс. Регулярний симплекс в n - мірному просторі являє собою багатогранник, утворений n 1 рівновіддаленими одна від одної точками

- вершинами.

Означення: Правильним симплексом в просторі En називається множина з n+1 рівновіддалених одна від одної точок (вершин симплекса). Відрізок, що з’єднує дві вершини, називається ребром симплекса.

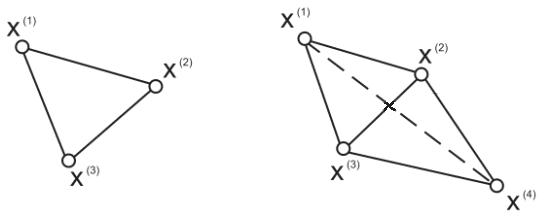
Для прикладу, в разі двох змінних симплексом є рівносторонній трикутник, а в тривимірному просторі симплекс являє собою тетраедр (рис.5.6).

Рис.5.6. Приклади симплексів для двовимірної та тривимірної областей

В алгоритмі симплексного пошуку використовується важлива властивість симплексів, згідно з чим новий симплекс можна побудувати на будь-якій грані початкового симплекса шляхом перенесення вибраної вершини на належну відстань вздовж прямої, яка проведена через центр ваги інших вершин початкового симплекса та початкову точку. Отримана таким чином нова точка є вершиною нового симплекса, а вибрана при побудові вершина початкового симплекса виключається. Неважко побачити, що при переході до нового симплекса потрібно одне обчислення значення цільової функції. Рис. 5.7

50