2.4.2. Діапазонні властивості.

Діапазон робочих частот антени являється інтервал частот від f_мін до f_макс, в якому ні один параметр не виходить за задані межі.

Інтервал називають смугою робочих частот, а частоту– середньою частотою. Смугаповинна бути не меншою ширини спектру коливань, випромінюваних антеною. Поділ антен в залежності від відносної ширини смугиприведено на рис. 2.7.

Широкодіапазонні антени також характеризують коефіцієнтом перекриття діапазону:

(2.22)

Додаток 2.1.

Потужність випромінювання та параметри , що визначаються на її основі

Потужність випромінювання. Потужність випромінювання антен представляє самостійний інтерес та є основою для визначення інших параметрів. Для її визначення доцільно розташувати антену в центрі сфери достатньо великого радіуса r (значно більшого за максимальні розміри антени та довжину хвилі, на якій використовується антена):

Рис. Д.2.1. До визначення потужності випромінювання антен

Потужність випромінювання визначається [ ] на основі методу вектора Пойтінга:

(Д.2.1)

де П_ср – середнє за період значення вектора Пойтінга; dS– добуток елемента поверхні dS і одиночного вектора нормалі до неї r_o ;

Визначивши окремі складові залежності (Д.2.1), отримаємо значення потужності випромінювання:

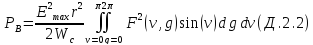
де W_c– хвильовий опір середовища (W_c = W₀ =120π, Ом – для вакууму).

Для багатьох антен нормована ДС не залежить від кута g. В даному випадку визначення потужності випромінювання спрощується:

Залежності (Д.2.2), (Д.2.3) є фундаментальними для подальшого дослідження антен.

Доведення залежності (Д.2.2). Спочатку розглянемо кожну складову залежності (Д.2.1).

Середнє за період значення вектора Пойтінга. Вказане значення визначається наступним чином:

(Д.2.4)

де – вектор Пойтінга.

Комплексний вектор Пойтінга в кожній точці вказаної сфери (радіусом r) становить:

де r_o – орт сферичної системи координат;,- спряжені значення комплексної величини магнітної та електричної складової напруженості поля, відповідно;.

Нехай на поверхні сфери радіусом r максимальне значення напруженості електричного поля становить Е_max. Тоді згідно залежності (1.??) напруженість поля в будь-якій точці поверхні сфери становить:

(Д.2.6)

На основі залежності (Д.2.4) з врахуванням (Д.2.5), (Д.2.6) отримаємо середнє значення вектора Пойтінга:

Площа елемента поверхні. Визначимо площу dS елемента поверхні сфери (рис.Д.2.1) .

Рис.Д.2.2. Визначення площі dS малої частини сферичної поверхні

Видно, що площа малої частини сферичної поверхні (при r>>1) становить:

(Д.2.8)

де, ; .

Отже, площа елемента поверхні становить:

(Д.2.9)

Вектор dS (Д.2.1) спрямований по нормалі до поверхні S, тому його напрям збігається з напрямом радіуса-вектора r. З врахуванням вказаного та залежностей (Д.2.7), (Д.2.9) отримаємо потужність випромінювання:

Представивши напруженість поля через нормовану ДС (Д.2.6) отримаємо шукану залежність (Д.2.2).

Використання Рв для визначення КСД. На основі даних про потужність випромінювання антени визначається один з найбільш важливих параметрів антен – КСД.

Доведення залежності (2.8). Врахуємо, що кутова густина потужності випромінювання антени визначається як відношення випромінюваної потужності Р_В до тілесного кута (вимірюється в стерадіанах). Тоді значення р(v,g) (2.7) можна перетворити наступним чином:

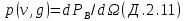
де - елемент тілесного кута.

Площа dS елемента поверхні (Д.2.9) пропорційна квадрату її віддалі r² до початку координат. Елемент тілесного кута визначимо, як нормовану (відносно r²) площу елемента поверхні:

(Д.2.12)

Враховуючи значення потужності випромінювання (Д.2.2) та залежність

(Д.2.12) отримаємо

Аналогічно для сфери радіусом r ,площа якої 4πr², тілесний кут становить 4π (4πr²/ r²). Тому для ІА отримаємо:

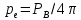(Д.2.14)

Підставляючи значення (Д.2.13), (Д.2.14) в залежність (2.7) з врахуванням потужності Р_В (Д.2.2) отримаємо шукану залежність (2.8) .

Доведення залежності (2.14). Для ізотропної антени повну потужність випромінювання антени можна визначити як добуток кутової густини потужності (Д.2.13) на просторовий кут 4π:

На основі залежності (Д.2.15) з врахуванням (2.13) визначимо:

З врахуванням того, що для вільного простору W_c=120π та F(v,g)=1 ( для напрямку максимального випромінювання) отримаємо залежність (2.14).

Розглянемо взаємозв’язок між КСД та опором випромінювання R_ВП на прикладі СВ. Прийнявши в залежності (Д.5.12, Додаток 5.1) v=π/2 та W_с=120π Ом отримаємо:

(Д.2.17)