17

Роздід 3. Елементарні випромінювачі

3.1. Призначення елементарних випромінювачів

3.2. Диполь Герца

3.3. Елемент Гюйгенса

Контрольні питання

Роздід 3. Елементарні випромінювачі

3.1. Призначення елементарних випромінювачів

В розділі 1 було показано, яке велике значення для аналізу антени має її ДС. Тому виникає питання- як визначити ДС конкретної антени, що є досить складною задачею. І в вирішенні даної проблеми неоціненну допомогу надають елементарні випромінювачі.

Загальні відомості. Елементарні випромінювачі (в чистому виді) неможливо виготовити практично, тому вони не можуть використовуватись як реальні антени. Виникає логічне питання – для чого розглядати фіктивні випромінювачі?

Елементарні випромінювачі вже згадувались при проведені класифікації антен ( рис.1.2) . Вказано, що антени з неперервним розподілом поля можна розглядати, як нескінченну сукупність елементарних випромінювачів

а) б)

Рис.3.1. Антени з неперервним розподілом поля, як сукупність нескінченної кількості елементарних випромінювачів: лінійні (а); апертурні (б)

В лінійних антенах розмір поперечного перерізу значно менший за довжину хвилі. Виготовляються лінійні антени з провідників, або у вигляді щілин у металічних поверхнях. Кожному з вказаних типів лінійних антен відповідає свій елементарний випромінювач: для провідників – електричний диполь (диполь Герца) ; для щілин – елементарний щілинний випромінювач.

В апертурних антенах випромінювання відбувається через певну уявну поверхню, яка розділяє внутрішній об’єм антени та зовнішній простір. Така поверхня є апертурою або розкривом та переважно представляє собою площину. І для апертурних антен також наявний елементарний випромінювач – елемент Гюйгенса.

Отже, основна цінність елементарних випромінювачів полягає в тому, що будь-яку реальну антену можна розглядати як сукупність великої кількості елементарних випромінювачів. Далі на основі ДС елементарних випромінювачів ( яка визначається відносно просто) можна визначити ДС реальної антени.

3.2. Диполь Герца

Будова. Його будова приведена на рис. 1.9. ДГ являє собою випромінювач, що складається з відрізкa провідника довжиною L_d та максимальним розміром поперечного перерізу S_d

а) б)

Рис. 1.9. Диполь Герца: будова (а); розміщення при визначенні ДС (б)

Віссю антен є одна (унікальна) пряма, що залежить від їх будови. Для ДГ віссю є пряма, що проходить вздовж його довжини. Отже, при визначенні ДС ДГ його вісь розміщується вздовж осі OZ, а середина (центр) ДГ –в початку осей координат.

Для ДГ повинні виконуватись три наступні умови

• довжина провідника Ld набагато менша за довжину хвилі (Ld‹‹λ);

• максимальний розмір поперечного перерізу також набагато менший за довжину хвилі (Sd‹‹λ);

• амплітуда струму одинакова вздовж його довжини (Id=const).

Очевидно, що реалізувати диполь Герца в «чистому» виді практично неможливо, тому що струм на кінцях провідника, згідно з законами збереження електрики, повинен бути рівним нулю.

Діаграма спрямованості. Як показано в Додатку 1.3 амплітуда напруженості електричного поля диполя Герца на значній віддалі r ( набагато більшій за його максимальні розміри та довжину хвиилі) визначається наступним чином

Е=n_d sin(v) (3.1)

де n_d=30kI_dL_d/r, k=2π/λ

Отже амплітудна ДС (як лише та складова, що залежить від кутів сферичної системи – в даному випадку тільки від кута v) становить sin(v), максимальне значення якої становить одиницю. В результаті отримаємо (дуже рідкий випадок) , що для диполя Герца амплітудна ДС та її нормоване значення рівні між собою

f(v) =F(v) = sin (v) – ДС за напруженістю поля (3.2,а)

fр(v) =Fр(v) = sin² (v) – ДС за потужністю (3.2,б)

Видно, що форму ДС ДГ неможливо змінити – вона не залежить від його геометричних розмірів. Графічне представлення отриманих ДС у виді просторових залежностей надає найбільш повну та наочну інформацію про характер випромінювання ДГ

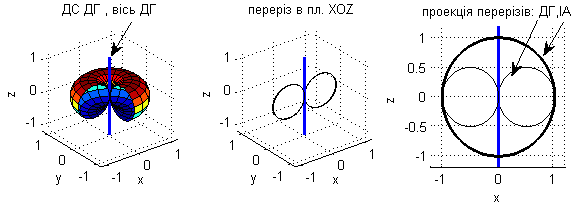
Рис.3.3. Просторова ДС ДГ в сферичній системі (нормована та ненормована) за напруженістю поля

Видно, що просторова ДС ДГ за напруженістю поля формується обертанням ДС (3.2,а) навколо його осі. Максимальне значення ДС ДГ рівне ДС ІА та становить 1. Аналогічно можна отримати просторову ДС за потужністю (3.2,б)

Рис.3.4. Просторова ДС СВ в сферичній системі (нормована та ненормована) за потужністю

Аналогічно, просторова ДС за потужністю формується обертанням ДС (3.2,б) навколо його осі. Максимальне значення ДС ДГ також рівне ДС ІА та становить 1.

Визначення ШГП. ДС ДГ (3.2,а,б) залежить від кута v, тобто є спрямованою лише у вертикальній площині (рис.3.3, рис.3.4). Вказану спрямованість можна оцінити значенням ШГП

Рис.3.5. Визначення ШГП ДГ на основі нормованої просторової ДС за напруженістю поля

Для визначення ШГП в залежності від кута v (за рівнем половинної потужності, 2v_0.5 ) також побудовано допоміжне коло радіусом 0.7. Точки перетину ДС ДГ з допоміжним колом визначають ШГП, яка в даному випадку становить, орієнтовно, 2v_0.5 ~ 90^о .

Аналогічно можна визначити ШГП на основі ДС за потужністю поля

Рис.3.6. Визначення ШГП ДГ на основі просторової ДС за потужністю поля

Для визначення ШГП (2v_0.5) побудовано допоміжне коло радіусом 0.5. Видно, що в даному випадку ШГП (2v_0.5 ) також становить орієнтовно 90^о. Отже, незважаючи на відмінності в формі ДС за напруженістю поля та потужністю, значення ШГП в обох випадках отримано одинакове.

Орієнтовне визначення коефіцієнта спрямованої дії. Враховуючи те, що ДС ДГ не залежить від кута g , то значення ШГП 2g_0.5 становить 360^о. На основі відомих значень ШГП ( 2v_0.5, 2g_0.5) для ІА та ДГ згідно залежності визначимо орієнтовно значення КСД

Кс~360*360/(360*90*2)=2 ( 3.3)

Примітка. При визначенні Кc (3.3) враховано те , що в ДС ДГ наявні дві головні пелюстки.

Значення коефіцієнта спрямованої дії. Даний коефіцієнт визначається згідно залежності за допомогою програми 3.1

Програма 3.1.

F=inline('(sin(v)).^2.*sin(v)','v')

[I,cnt]=quad(F,0,pi,10^-5)

D0=2/I

Kcd=10*log10(D0)

В результаті для диполя Герца отримаємо

Do=1.5 або Do=1.76 дБ (3.4)

Причини збільшення КСД для ДГ (порівняно з ІА) видно на основі ДС (рис.3.3, рис.3.4) - ДС для ДГ все таки мають певну (хоч і незначну) спрямованість.

Інші представлення ДС. Крім розглянутих ДС також може бути доцільним використання суміщених просторових ДС для ДГ. Такі ДС містять власне нормовану просторову ДС та її перерізи в головних площинах, але розміщення перерізів збережено в тих площинах просторової ДС, де вони були отримані

Рис.3.8. ДС (суміщена, нормована, за напруженістю поля) диполя Герца в сферичній системі та отримані на її основі ДС

Така ДС надає більш наглядну інформацію про її перерізи, тобто автоматично формує їх на площині в полярній системі. Також на проекції на площину XOZ приведено додаткове коло r=0.7, необхідне для визначення ШГП.

Нормована просторова ДС в прямокутній системі. Крім просторової ДС в полярній системі також може використовуватись аналогічна ДС в прямокутній системі

Рис.3.9. Нормована просторова ДС ДГ за напруженістю поля в прямокутній системі та її проекція на площину ( F(v), v)

Фактично проекція просторової ДС СВ на площину (F(v), v) автоматично формує ДС СВ на площині в прямокутній системі, яку немає необхідності будувати додатково. Також з отриманої ДС просто визначити ШГП 2v_0.5, яка в даному випадку становить: 2v_0.5=135^о-45^о=90^о

ДС на площині можна також отримати безпосередньо не використовуючи просторові ДС.

Нормовані ДС ДГ на площині в полярній системі. Такі ДС можуть бути представлені за напруженістю та потужністю

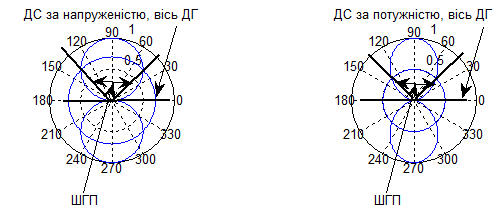
Рис.3.10. Нормовані ДС ДГ в полярній системі та визначення ШГП

Приведені ДС отримані нам основі програми 3.2.

Програма 3.2

figure ('Color','w');

v=[0:pi/115:2*pi];

subplot(2,2,1);F=abs(sin(v));polar(v,F);hold on;

rd=0.7*v./v;polar(v,rd);hold on;title('ДС за напруженістю, вісь ДГ');

subplot(2,2,2);Fp=sin(v).^2;polar(v,Fp);hold on;

rd=0.5*v./v;polar(v,rd);hold on;title('ДС за потужністю, вісь ДГ');

Видно, що ДС в обох випадках дещо відрізняються. Для визначення ШГП 2v_0.5 в ДС за напруженістю поля (потужністю) необхідно побудувати допоміжне коло радіусом 0.7 (0.5). В результаті отримаємо ШГП в обох випадках однаковою.

Нормовані ДС ДГ на площині в прямокутній системі. Такі ДС також можуть бути представлені за напруженістю та потужністю

Рис.3.8. Нормовані ДС ДГ в прямокутній системі та визначення ШГП

Приведені ДС отримані нам основі програми 3.3.

Програма 3.3

figure ('Color','w');

v1=[0:180/500:2*180]; v=pi/180*v1

subplot(2,2,1);F=abs(sin(v));plot(v1,F);hold on;

rd=0.7*v./v;plot(v1,rd);hold on; grid on;title('ДС за напруженістю, ШГП');

axis([0 360 0 1.2]);xlabel('v');ylabel('F(v)');

subplot(2,2,2);Fp=sin(v).^2;plot(v1,Fp);hold on;

rd=0.5*v./v;plot(v1,rd); grid on;hold on;title('ДС за потужністю, ШГП');

axis([0 360 0 1.2]);xlabel('v');ylabel('Fp(v)');

Видно, що ДС в обох випадках дещо відрізняються. Для визначення ШГП 2v_0.5 в ДС за напруженістю поля (потужністю) необхідно побудувати допоміжні лінії F(v)=0.7 (F(v)=0.5). В результаті отримаємо одинакове значення ШГП в обох випадках.