
- •4. Симетричний вібратор ……………………………….1
- •4. Симетричний вібратор
- •4.1. Призначення та застосування
- •4.2. Будова св та визначення дс
- •4.3 Визначення шгп
- •5.3. Вибір довжини св та коефіцієнт спрямованої дії
- •5.4. Графічне представлення дс та визначення шгп
- •5.5. Інші параметри св
- •5.5.1. Опір випромінювання
- •4.3.1. Діюча довжина
- •4.3.2. Опір випромінювання.
- •4.3.1. Опір випромінювання
- •4.3.2. Вхідний опір
- •4.3.4. Діюча довжина.
- •4.3.2. Вхідний опір
5.4. Графічне представлення дс та визначення шгп
Спочатку розглянемо ДС на площині.
Нормовані ДС в полярній системі за напруженістю поля. Розглянемо такі ДС для різних значень Ln

Рис.5.12. ДС F(v) для СВ в полярній системі при різних значеннях Ln
Приведені ДС отримані на основі програми 2.1
Програма 2.1.
figure ('Color','w');a=115;
va=0;vb=2*pi; vba=vb-va; v=(va:vba/a:vb)
for k=[1 2 3]
subplot(2,3,k);
if k==1; Ln=0.25;
elseif k==2; Ln=0.5;
else Ln=0.625;
end
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2)*sin(v);
F=abs(b3./b4);polar(v,F);
end
subplot(2,3,1);title('вісь СВ, Ln=0.25');
subplot(2,3,2);title('вісь СВ, Ln=0.5');
subplot(2,3,3);title('вісь СВ, Ln=0.625');
Видно, що при збільшені Ln ШГП стає вужчою, але виникають БП.
Нормовані ДС в полярній системі за кутовою густиною потужності. Нижче приведені такі ДС для різних значень Ln
figure ('Color','w');a=115;
va=0;vb=2*pi; vba=vb-va; v=(va:vba/a:vb)
for k=[1 2 3]
subplot(2,3,k);
if k==1; Ln=0.25;
elseif k==2; Ln=0.5;
else Ln=0.625;
end
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2)*sin(v);
F=abs(b3./b4);polar(v,F.^2);
end
subplot(2,3,1);title('вісь СВ,Ln=0.25');
subplot(2,3,2);title('вісь СВ,Ln=0.5');
subplot(2,3,3);title('вісь СВ,Ln=0.625');

Рис.5.13. ДС F2(v) для СВ при різних значеннях Ln
Видно, що ГП вужча для ДС F2(v) порівняно з ДС F(v). На основі приведених ДС можна визначити ШГП (2v0.5)
figure ('Color','w');Ln=0.5;
a=115;va=0;vb=2*pi; vba=vb-va; v=(va:vba/a:vb);
subplot(2,2,1);
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2)*sin(v);F=abs(b3./b4);
polar(v,F);hold on;polar(v,0.7*v./v,'--');title('Ln=0.5');
subplot(2,2,2);
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2)*sin(v);F=abs(b3./b4);
polar(v,F.^2);hold on;polar(v,0.5*v./v,'--');title(' Ln=0.5');

Рис.5.14. ДС для СВ при Ln=0.5: F(v) (a); F2(v) (б)
На нормованих ДС за напруженістю поля приведено допоміжне коло радіусом 0.7, а на ДС за кутовою густиною потужності - радіусом 0.5. Видно, що ДС в обох випадках ШГП (2v0.5) становить,орієнтовно, менше 60о
Нормовані ДС в прямокутній системі за напруженістю поля. ДС на площині також можуть бути приведені в прямокутній системі
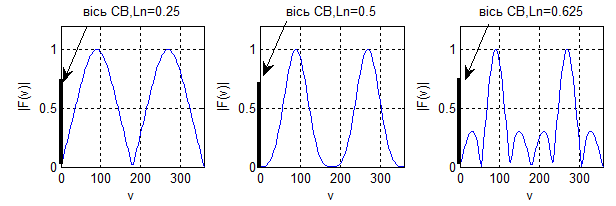
Рис.5.15. ДС F(v) для СВ в прямокутній системі при різних значеннях Ln
Приведені ДС отримані на основі програми 2.2
Програма 2.2
figure ('Color','w');a=115;
va=0;vb=360; vba=vb-va; v1=(va:vba/a:vb);v=pi/180*v1;
for k=[1 2 3]
subplot(2,3,k);
if k==1; Ln=0.25;
elseif k==2; Ln=0.5;
else Ln=0.625;
end
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2)*sin(v);
F=abs(b3./b4);plot(v1,F);axis([0 360 0 1.2]);grid on;
xlabel('v');ylabel('|F(v)|');
end
subplot(2,3,1);title('вісь СВ,Ln=0.25');
subplot(2,3,2);title('вісь СВ,Ln=0.5');
subplot(2,3,3);title('вісь СВ,Ln=0.625');
Вказані ДС можна привести в логарифмічному масштабі
figure ('Color','w');a=115;
va=0;vb=360; vba=vb-va; v1=(va:vba/a:vb);v=pi/180*v1;
for k=[1 2 3]
subplot(2,3,k);
if k==1; Ln=0.25;
elseif k==2; Ln=0.5;
else Ln=0.625;
end
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2)*sin(v);
F=10*log10(abs(b3./b4));plot(v1,F);axis([0 360 0 1.2]);grid on;
axis([0 360 -20 0.2]);xlabel('v');ylabel('|F(v)|, дБ');
end
subplot(2,3,1);title('Ln=0.25');
subplot(2,3,2);title('Ln=0.5');
subplot(2,3,3);title('Ln=0.625');

Рис.5.16. ДС F(v) для СВ в прямокутній системі та логарифмічному масштабі
На основі ДС в логарифмічному масштабі краще видно рівень БП.
Нормовані ДС в прямокутній системі за кутовою густиною потужності . Аналогічні ДС, як і за напруженістю поля, можна отримати за кутовою густиною потужності.

Рис.5.17. ДС F2(v) для СВ в прямокутній системі при різних значеннях Ln
Також аналогічні ДС можна привести в логарифмічному масштабі
figure ('Color','w');a=115;
va=0;vb=360; vba=vb-va; v1=(va:vba/a:vb);v=pi/180*v1;
for k=[1 2 3]
subplot(2,3,k);
if k==1; Ln=0.25;
elseif k==2; Ln=0.5;
else Ln=0.625;
end
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2)*sin(v);
F=20*log10(abs(b3./b4));plot(v1,F);axis([0 360 0 1.2]);grid on;
axis([0 360 -20 0.2]);xlabel('v');ylabel('|F(v)|, дБ');
end
subplot(2,3,1);title('Ln=0.25');
subplot(2,3,2);title('Ln=0.5');
subplot(2,3,3);title('Ln=0.625');

Рис.5.18. ДС F2(v) для СВ в прямокутній системі та логарифмічному масштабі
Використовуючи ДС в прямокутній системі також можна визначити ШГП (2v0.5)
figure ('Color','w');a=115;
va=0;vb=180; vba=vb-va; v1=(va:vba/a:vb);v=pi/180*v1;
subplot(2,2,1);
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2)*sin(v);
F=(abs(b3./b4));plot(v1,F);hold on;plot(v1,0.7*v1./v1);hold on;grid on;
axis([0 180 0 1.2]);xlabel('v');ylabel('|F(v)|');title('Ln=0.625');
subplot(2,2,2);
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2)*sin(v);
F=(abs(b3./b4));plot(v1,F.^2);hold on;plot(v1,0.5*v1./v1);hold on;grid on;
axis([0 180 0 1.2]);xlabel('v');ylabel('F^2(v)');title('Ln=0.625');
subplot(2,2,3);
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2)*sin(v);
F=10*log10(abs(b3./b4));plot(v1,F);hold on;plot(v1,-3*v1./v1);hold on;grid on;
axis([0 180 -20 0.2]);xlabel('v');ylabel('F(v),dB');title('Ln=0.625');
subplot(2,2,4);
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2)*sin(v);
F=20*log10(abs(b3./b4));plot(v1,F);hold on;plot(v1,-6*v1./v1);hold on;grid on;
axis([0 180 -20 0.2]);xlabel('v');ylabel('F^2(v),dB');title('Ln=0.625');

Рис.5.19. До визначення для СВ при Ln=0.625 ШГП (2v0.5) на основі ДС в прямокутній системі
ШГП (2v0.5) визначаються на основі нормованих ДС:
на рівні 0.7 – для ДС за напруженістю поля;
на рівні 0.5 – для ДС за кутовою густиною потужності;
на рівні -3dB – для ДС за напруженістю поля в логарифмічному масшабі;
на рівні -6dB – для ДС за кутовою густиною потужністю логарифмічному масшабі.
На основі ДС в лінійному масштабі видно, що 2v0.5≈106о-74о=32о.
Нормовані ДС в сферичній системі. Розглянемо далі просторові ДС, причому спочатку ДС в сферичній системі
figure ('Color','w');a=15;
gn=-pi/2; gv=pi;gvn=gv-gn; vn=0; vv=pi;vvn=vv-vn; a=15;
[g, v]=meshgrid(gn:gvn/a:gv, vn:vvn/a:vv);
for k=[1 2 3]
subplot(2,3,k);
if k==1; Ln=0.25;
elseif k==2; Ln=0.5;
else Ln=0.625;
end
b1=2*pi*Ln; b2=cos(b1);
b3=cos(b1.*cos(v))-b2;b4=(1-b2).*sin(v);F=abs(b3./b4);
x=F.*sin(v).*cos(g); y=F.*sin(v).*sin(g); z=F.*cos(v).*(g+1)./(g+1);
surf(x,y,z);hold on; xlabel('x'); ylabel('y ');zlabel('z ');hold on;
t = 0:0.01:2.4; plot3(t./t-1,t./t-1,t-1.2,'LineWidth',2 );
axis([-1.2 1.2 -1.2 1.2 -1.2 1.2]);
end
subplot(2,3,1);title('Ln=0.25');
subplot(2,3,2);title('Ln=0.5');
subplot(2,3,3);title('Ln=0.625');

Рис.5.19. ДС F(v) для СВ в сферичній системі при різних значеннях Ln
Видно, що при Ln=0.625 вже наявні БП незначного рівня.
Суміщені нормовані ДС в сферичній системі. Більш інформативними є суміщені ДС

Рис.5.20. Нормована ДС СВ в сферичній системі (суміщена, вісь СВ орієнтована вздовж осі ОZ) при Ln=0.5 та отримані на її основі ДС
Видно, що суміщена ДС містить інформацію як про просторову ДС, так про її перерізи в головних площинах (що проходять через напрям максимального випромінювання).
Але при аналізі АР можуть бути випадки, коли вісь СВ орієнтована інакше, наприклад, вздовж осі ОХ
figure ('Color','w'); Ln=0.5;
for k= [1 3 4 5 6]
subplot(2,3,k); a=150;a1=15
[g, v]=meshgrid(0:pi/a:pi/a, 0:pi/a:2*pi);
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2).*sin(v);F=abs(b3./b4);
y=F.*sin(v).*cos(g); z=F.*sin(v).*sin(g); x=F.*cos(v).*(g+1)./(g+1);
surf(x,y,z-1.2);hold on;
[g, v]=meshgrid(pi/2:pi/a:pi/2+pi/a, 0:pi/a:2*pi);
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2).*sin(v);F=abs(b3./b4);
y=F.*sin(v).*cos(g); z=F.*sin(v).*sin(g); x=F.*cos(v).*(g+1)./(g+1);
surf(x,y+1.2,z);hold on;
[g, v]=meshgrid(0:pi/a:2*pi, pi/2:pi/a:pi/2+pi/a);
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2).*sin(v);F=abs(b3./b4);
y=F.*sin(v).*cos(g); z=F.*sin(v).*sin(g); x=F.*cos(v).*(g+1)./(g+1);
surf(x+1.2,y,z);hold on;
t = 0:0.01:2.4; plot3(t-1.2,t./t-1,t./t-1,'LineWidth',2 );hold on;
xlabel('x'); ylabel('y ');zlabel('z '); axis([-1.2 1.2 -1.2 1.2 -1.2 1.2]);
end
for p= [1 2]
subplot(2,3,p); [g, v]=meshgrid(0:pi/a1:2*pi, 0:pi/a1:pi);
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2).*sin(v);F=abs(b3./b4);
y=F.*sin(v).*cos(g); z=F.*sin(v).*sin(g); x=F.*cos(v).*(g+1)./(g+1);
surf(x,y,z);hold on;
t = 0:0.01:2.4; plot3(t-1.2,t./t-1,t./t-1,'LineWidth',2 );hold on;
xlabel('x'); ylabel('y ');zlabel('z ');axis([-1.2 1.2 -1.2 1.2 -1.2 1.2]);
end
subplot(2,3,1); title('суміщена ДС');subplot(2,3,2);title('просторова ДС');
subplot(2,3,3); title('перерізи ДС');subplot(2,3,4);title('проекція на XOY');
subplot(2,3,5); title('проекція на XOZ');subplot(2,3,6);title('проекція на YOZ');

Рис.5.21. Нормована ДС СВ в сферичній системі (суміщена, вісь СВ орієнтована вздовж осі ОХ) при Ln=0.5 та отримані на її основі ДС
Аналогічно вісь СВ може бути орієнтована вздовж осі ОY
figure ('Color','w'); Ln=0.5;
for k= [1 3 4 5 6]
subplot(2,3,k); a=150;a1=15;
[g, v]=meshgrid(0:pi/a:pi/a, 0:pi/a:2*pi);
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2).*sin(v);F=abs(b3./b4);
z=F.*sin(v).*cos(g); x=F.*sin(v).*sin(g); y=F.*cos(v).*(g+1)./(g+1);
surf(x+1.2,y,z);hold on;
[g, v]=meshgrid(pi/2:pi/a:pi/2+pi/a, 0:pi/a:2*pi);
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2).*sin(v);F=abs(b3./b4);
z=F.*sin(v).*cos(g); x=F.*sin(v).*sin(g); y=F.*cos(v).*(g+1)./(g+1);
surf(x,y,z-1.2);hold on;
[g, v]=meshgrid(0:pi/a:2*pi, pi/2:pi/a:pi/2+pi/a);
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2).*sin(v);F=abs(b3./b4);
z=F.*sin(v).*cos(g); x=F.*sin(v).*sin(g); y=F.*cos(v).*(g+1)./(g+1);
surf(x,y+1.2,z);hold on;
t = 0:0.01:2.4; plot3(t./t-1,t-1.2,t./t-1,'LineWidth',2 );hold on;
xlabel('x'); ylabel('y ');zlabel('z '); axis([-1.2 1.2 -1.2 1.2 -1.2 1.2]);
end
for p= [1 2]
subplot(2,3,p); [g, v]=meshgrid(0:pi/a1:2*pi, 0:pi/a1:pi);
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=(1-b2).*sin(v);F=abs(b3./b4);
z=F.*sin(v).*cos(g); x=F.*sin(v).*sin(g); y=F.*cos(v).*(g+1)./(g+1);
surf(x,y,z);hold on;
t = 0:0.01:2.4; plot3(t./t-1,t-1.2,t./t-1,'LineWidth',2 );hold on;
xlabel('x'); ylabel('y ');zlabel('z ');axis([-1.2 1.2 -1.2 1.2 -1.2 1.2]);
end
subplot(2,3,1); title('суміщена ДС');subplot(2,3,2);title('просторова ДС');
subplot(2,3,3); title('перерізи ДС');subplot(2,3,4);title('проекція на XOY');
subplot(2,3,5); title('проекція на XOZ');subplot(2,3,6);title('проекція на YOZ');
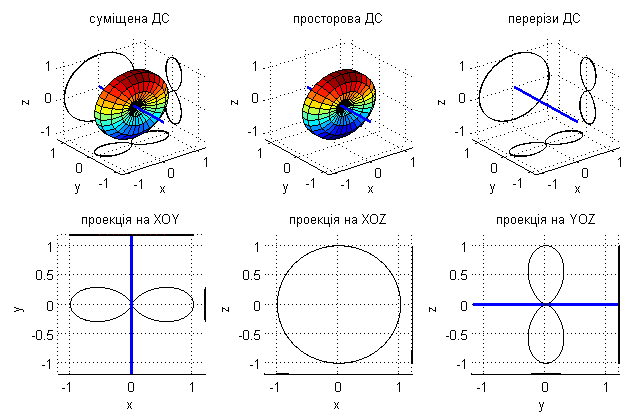
Рис.5.22. Нормована ДС СВ в сферичній системі (суміщена, вісь СВ орієнтована вздовж осі ОY) при Ln=0.5 та отримані на її основі ДС
Таким чином, сформовано набір просторових нормованих ДС СВ при орієнтації їх осі вздовж довільної осі (OX, OY, OZ) системи координат. Такі суміщені ДС з різною орієнтацією осі СВ використовуються в подальшому, при розгляді АР .
Нормовані ДС за напруженістю поля в прямокутній системі (просторові) та визначення ШГП. Використовуючи просторові ДС в прямокутній системі можна просто визначити ШГП
figure ('Color','w'); Ln=0.5;
for k=[1:3];
if k==1; Fa=0.7;a=20;
elseif k==2; Fa=0.7;a=500;
else Fa=0.7;a=500;
end
va=0;vb=360; vba=vb-va;
subplot(2,3,k);[v,g ]=meshgrid(va:vba/a:vb, va:vba/a:vb);
b1=2*pi*Ln;b2=cos(b1);b3=cos(b1.*cos(v.*pi/180))-b2;b4=(1-b2).*sin(v.*pi/180);
F=(g+1)./(g+1).*(abs(b3./b4)); surf(v,g,F);hold on;
Fd=Fa*(v+1)./(v+1).*(g+1)./(g+1); surf(v,g,Fd);
xlabel('v');ylabel('g ');
zlabel('|F(v)|');axis([0 360 0 360 0 1.2]);
end
subplot(2,3,1);title('ДС, площина F(v)=0.7');
subplot(2,3,2);title('ДС, площина F(v)=0.7');
subplot(2,3,3);title('ДС, площина F(v)=0.7');axis([50 130 0 360 0 1.2]);

а) б) в)
Рис.5.23. ДС СВ при Ln =0.625 (просторова, в прямокутній системі, з допоміжною площиною ) та її проекція на площину (v - |F(v)| ) при різних масштабах (б, в)
З приведених ДС можна визначити ШГП (2v0.5), яка становить 106о-73о=33о . Також можна визначити рівень, який становить 0.3 (при Ln=0.625) від рівня ГП.
Комбіновані ДС. Комбіновані ДС для СВ в сферичній системі приведені на рис.1.26. На основі комбінованих ДС в прямокутній системі можна визначити залежність 2v0.5=f(Ln). В нормованій ДС за напруженістю поля рівень 0.7 вказує на ШГП (2v0.5). Тому для визначення ШГП в комбінованій нормованій ДС необхідно спочатку провести допоміжну площину на рівні 0.7
figure ('Color','w');
for k=[1:2];
if k==1; a=20;Lna=0.01;Lnb=0.7;va=0;vb=360;
else a=20;Lna=0.01;Lnb=0.7;va=0;vb=90;
end
vba=vb-va;Lba=Lnb-Lna;
subplot(2,2,k);[v,Ln ]=meshgrid(va:vba/a:vb, Lna:Lba/a:Lnb);
b1=2*pi*Ln;b2=cos(b1);b3=cos(b1.*cos(v.*pi/180))-b2;b4=(1-b2).*sin(v.*pi/180);
F=abs(b3./b4); surf(v,Ln,F);hold on;
xlabel('v');ylabel('Ln ');zlabel('F(v)');axis([va vb 0 0.7 0 1.2]);
end
for k=[3:4];
if k==3; a=500;Lna=0.01;Lnb=0.7;va=0;vb=360;
else a=500;Lna=0.01;Lnb=0.7;va=40;vb=90;
end
vba=vb-va;Lba=Lnb-Lna;
subplot(2,2,k);[v,Ln ]=meshgrid(va:vba/a:vb, Lna:Lba/a:Lnb);
b1=2*pi*Ln;b2=cos(b1);b3=cos(b1.*cos(v.*pi/180))-b2;b4=(1-b2).*sin(v.*pi/180);
F=abs(b3./b4); surf(v,Ln,F);hold on;
xlabel('v');ylabel('Ln ');zlabel('F(v)');axis([va vb 0 0.7 0 1.2]);
end
for k=[1:2];
if k==1; a=20;Lna=0.01;Lnb=0.7;Fa=0.7;va=0;vb=360;
else a=20;Lna=0.01;Lnb=0.7;Fa=0.7;va=0;vb=90;
end
vba=vb-va;Lba=Lnb-Lna;
subplot(2,2,k);[v,Ln ]=meshgrid(va:vba/a:vb, Lna:Lba/a:Lnb);
Fd=Fa*(v+1)./(v+1).*(Ln+1)./(Ln+1); surf(v,Ln,Fd);hold on;
surf(v,Ln,Fd);xlabel('v');ylabel('Ln ');
zlabel('F(v)');axis([va vb 0 0.7 0 1.2]);
end
for k=[3:4];
if k==3; a=50;Lna=0.01;Lnb=0.7;Fa=0.7;va=0;vb=360;
else a=50;Lna=0.01;Lnb=0.7;Fa=0.7;va=40;vb=90;
end
vba=vb-va;Lba=Lnb-Lna;
subplot(2,2,k);[v,Ln ]=meshgrid(va:vba/a:vb, Lna:Lba/a:Lnb);
Fd=Fa*(v+1)./(v+1).*(Ln+1)./(Ln+1); surf(v,Ln,Fd);hold on;
surf(v,Ln,Fd);xlabel('v');ylabel('Ln ');
zlabel('F(v)');axis([va vb 0 0.7 0 1.2]);
end
subplot(2,2,1);title('БП,ГП, додаткова площина');
subplot(2,2,2);title('БП,ГП, додаткова площина');
subplot(2,2,3);title('БП,ГП,проекція на пл. "v,Ln"');
subplot(2,2,4);title('БП,ГП, проекція на пл. "v,Ln"');

а)

б)
Рис. 5.24. Нормована ДС СВ за напруженістю поля: комбінована, в прямокутній системі (а); проекція на площину «v-Ln» (б)
Проекція даної ДС на площину «v-Ln» (рис.5.7,б) якраз і формує графічну залежність ШГП 2v0.5=f(Ln). Видно, що при виконанні умови
0.3<Ln<0.7 (5.12)
дана залежність практично лінійна. На основі даних (рис.5.24, б) можна визначити аналітичні залежності для ШГП (як рівняння прямої, що проходить через дві точки)
(Ln- Lna)/ (Lnb - Lna) = (v0.5 - v0.5a)/ |(v0.5b - v0.5a) | ( 5.13 )
де Lna=0.3; Lnb=0.7; v0.5a~90o-53o=37o; v0.5b~90o-78o=12o
На основі залежності (5.13) отримаємо значення ШГП (2v0.5) для СВ
2v0.5= -124.9Ln +111.5 (град) при 0.3≤ Ln ≤0.7 (5.14)
Нижче приведено графічне відображення залежності (5.14)
figure ('Color','w'); Lna=0.3;Lnb=0.7; a=100; Ln=Lna:(Lnb-Lna)/a:Lnb;
s2=111.5*(1-1.12*Ln);subplot(2,1,1);plot(Ln,s2); grid on;
axis([0.25 0.75 0 90]);xlabel('Ln ');ylabel('2v_0_._5');

Рис. 5.25. Залежність ШГП від нормованої довжини Ln плеча СВ.
Видно, що для найбільш характерних видів СВ, нормована довжина Ln яких 0.5 та 0.625, ШГП (2v0.5) становить,орієнтовно, 49 та 34 градуси, відповідно.
Залежність (5.14) та її графічне представлення (рис.5.25) також враховуються при виборі значення Ln.
Визначення залежності ШГП (2v0.1) від Ln. Вище (рис. 5.7) приведена залежність для ШГП 2v0.5=f(Ln). Також представляє інтерес визначення неперервної залежності ШГП 2v0.1=f(Ln), тобто на рівні 0.1 від максимального значення
figure ('Color','w');
for k=[1:2];
if k==1; a=20;Lna=0.01;Lnb=0.7;va=0;vb=360;
else a=20;Lna=0.01;Lnb=0.7;va=0;vb=90;
end
vba=vb-va;Lba=Lnb-Lna;
subplot(2,2,k);[v,Ln ]=meshgrid(va:vba/a:vb, Lna:Lba/a:Lnb);
b1=2*pi*Ln;b2=cos(b1);b3=cos(b1.*cos(v.*pi/180))-b2;b4=(1-b2).*sin(v.*pi/180);
F=abs(b3./b4); surf(v,Ln,F);hold on;
xlabel('v');ylabel('Ln ');zlabel('F(v)');axis([va vb 0 0.7 0 1.2]);
end
for k=[3:4];
if k==3; a=100;Lna=0.01;Lnb=0.7;va=0;vb=360;
else a=100;Lna=0.01;Lnb=0.7;va=0;vb=90;
end
vba=vb-va;Lba=Lnb-Lna;
subplot(2,2,k);[v,Ln ]=meshgrid(va:vba/a:vb, Lna:Lba/a:Lnb);
b1=2*pi*Ln;b2=cos(b1);b3=cos(b1.*cos(v.*pi/180))-b2;b4=(1-b2).*sin(v.*pi/180);
F=abs(b3./b4); surf(v,Ln,F);hold on;
xlabel('v');ylabel('Ln ');zlabel('F(v)');axis([va vb 0 0.7 0 1.2]);
end
for k=[1:2];
if k==1; a=20;Lna=0.01;Lnb=0.7;Fa=0.05;va=0;vb=360;
else a=20;Lna=0.01;Lnb=0.7;Fa=0.05;va=0;vb=90;
end
vba=vb-va;Lba=Lnb-Lna;
subplot(2,2,k);[v,Ln ]=meshgrid(va:vba/a:vb, Lna:Lba/a:Lnb);
Fd=Fa*(v+1)./(v+1).*(Ln+1)./(Ln+1); surf(v,Ln,Fd);hold on;
surf(v,Ln,Fd);xlabel('v');ylabel('Ln ');
zlabel('F(v)');axis([va vb 0 0.7 0 1.2]);
end
for k=[3:4];
if k==3; a=50;Lna=0.01;Lnb=0.7;Fa=0.05;va=0;vb=360;
else a=50;Lna=0.01;Lnb=0.7;Fa=0.05;va=0;vb=90;
end
vba=vb-va;Lba=Lnb-Lna;
subplot(2,2,k);[v,Ln ]=meshgrid(va:vba/a:vb, Lna:Lba/a:Lnb);
Fd=Fa*(v+1)./(v+1).*(Ln+1)./(Ln+1); surf(v,Ln,Fd);hold on;
surf(v,Ln,Fd);xlabel('v');ylabel('Ln ');
zlabel('F(v)');axis([va vb 0 0.7 0 1.2]);
end
subplot(2,2,1);title('БП,ГП, додаткова площина');
subplot(2,2,2);title('БП,ГП, додаткова площина');
subplot(2,2,3);title('БП,ГП,проекція на пл. "v,Ln"');
subplot(2,2,4);title('БП,ГП, проекція на пл. "v,Ln"');

а) б)

в) г)
Рис.5.26. Комбіновані ДС СВ в прямокутній системі за напруженістю поля, їх переріз додатковою площиною ( при F(v)=0) та проекції даних перерізів на площину «v-Ln»
На основі даних (рис.5.17) аналогічно (5.8) можна визначити аналітичні залежності для ШГП (як рівняння прямої, що проходить через дві точки)
(Ln- Lna)/ (Lnb - Lna) = (v0.5 - v0.5a)/ |(v0.5b - v0.5a) | ( 5.15 )
де Lna=0.4; Lnb=0.68; v0.5a~90o-13o=77o; v0.5b~90o-65o=25o

Рис. 5.27. Залежність ШГП 2v0.1 від нормованої довжини Ln плеча СВ.
Видно, що для найбільш характерних видів СВ, нормована довжина Ln яких 0.4, 0.5 та 0.625, ШГП (2v0.5)становить,орієнтовно, 154, 117 та 72 градуси, відповідно.
