5.2.3. Інші види дс множника ар.
Досі розглядались ДС множника АР лише на площині – в полярній системі. Варто зауважити, що для кращого представлення та розуміння отриманих результатів використовувалось сімейство характеристик при фіксованих значеннях одного з параметрів (наприклад, dn=const – dn1…dn4). Але такому представленню ДС властиві певні недоліки:
відома форма ДС тільки в одній площині, а при визначенні результуючої ДС АР часто необхідні дані про ДС в дво-трьох площинах;
при використанні сімейста характеристик збільшується об'єм досліджень та викладеного матеріалу;
можна невдало вибрати фіксовані значення dn=const та пропустити точки найбільш характерні для даних ДС;
труднощі точного визначення малих значень ШГП (наприклад, рис.5.8).
Представлення множника АР у виді просторової ДС. Просторовим ДС множника АР властиві певні переваги.
Рис.5.18. Множник АР: просторова ДС (вікно1); її перерізи (вікно 2) та їх проекція на площину XOZ (вікно 3); дані ( hn=0, dn=0.7, N=2) для АР (вікно 4).
Приведені ДС отримані на основі script-файлу s5n2 ( Додаток 5.3). Просторові залежності ДС використовуються також при формуванні результуючих ДС АР.
Представлення ДС множника АР з використанням просторових залежностей (вікно 1) та їх перерізів в площинах XOZ, YOZ, XOY (вікно 2) являється доволі інформативним та наглядним. При необхідності з отриманих перерізів просто отримати необхідну ДС на будь-якій (XOZ, YOZ, XOY ) площині (вікно 3, в даному випадку – на площині XOZ). Видно, обі ДС (рис.5.4, вікно 2 та рис. 5.17, вікно 3) повністю співпадають. Варто зауважити , що для надання більшої інформативності отриманим графічним залежностям приведені додаткові дані (вікно 4):
значення hn, dn та N, при яких отримані дані графічні залежності;
гранична лінія, тобто залежність dn кр (hn) в площині (dn, hn), правіше якої, згідно залежності (5.8, б) наявний не один головний пелюсток, а декілька.
З отриманих залежностей видно, що наявна система поперечного випромінювання, тобто головний пелюсток направлений нормально до осі АР.
Аналогічно (script-файл s5n2) отримано дані про характер зміни ДС множника АР при збільшенні параметру hn
Рис.5.19. Множник АР: просторова ДС (вікно1); її перерізи (вікно 2) та їх проекція на площину XOZ (вікно 3); дані ( hn=1, dn=0.4, N=2) АР (вікно 4).
Видно, що в даному випадку наявна система поздовжного випромінювання при наявності бокового пелюстка. Порівнюючи ДС (рис. 5.9, вікно 3 та рис.5.19, вікно 3) видно, що вони повністю співпадають.
Також аналогічно (script-файл s5n2) отримано дані про характер зміни ДС множника АР при 0<|hn|<1
Рис.5.20. Множник АР: просторова ДС (вікно1); її перерізи (вікно 2) та їх проекція на площину XOZ (вікно 3); дані ( hn=0.5, dn=0.54, N=4) АР (вікно 4).
Видно, що в даному випадку наявна система нахиленого випромінювання при наявності бокових пелюстків. Порівнюючи ДС (рис. 5.20, вікно 3 та рис.5.14, вікно 3) видно, що вони повністю співпадають.
Таким чином, просторові ДС являються більш інформативними та наглядними.
Динамічні ДС. При використанні динамічних ДС відпадає, в принципі, необхідність використання сімейства окремих ДС.
а)
б)
Рис. 5.21. Формування динамічних ДС множника АР (N=2, hn=0 ) .
Приведені ДС отримані за допомогою графічного інтерфейса g5n1 (Додаток 5.4 ). Динамічні ДС містять просторову ДС, її перерізи в площинах XOZ , YOZ (повертання одного з них навколо осі OZ якраз і формує просторову ДС) , переріз в площині XOY та ДС в полярній системі (площина XOZ).
Особливість динамічних ДС полягає в тому, що вони будуються майже в реальному часі шляхом зміни положення повзунка (після закінчення пересування повзунка та його відпускання, рис.5.21,б). Така можливість дозволяє оперативно та послідовно розглянути всі можливі варіанти ДС та вибрати оптимальне значення dn, на основі певної форми ДС.
ДС в прямокутній системі, на площині. ДС в прямокутній системі на площині дозволяють з довільною точністю визначити малі значення ШГП.
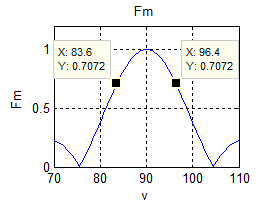
Рис.5.22. ДС множника АР в прямокутній системі (при N=8, dn=0.5, hn=0): а) повний діапазон зміни кута Ɵ; б) звужений діапазон – для визначення ШГП
Приведені ДС отримані на основі лістингу p5n2 (Додаток 5.1)
% лістинг p5n2
N=8; dn=0.5; hn=0; va=70; vb=110; n=100; var=va*pi/180; vbr=vb*pi/180;
vr = var:(vbr-var)/n:vbr; v = va:(vb-va)/n:vb;
u=pi*N*dn.*(cos(vr)-hn); Fm=abs(sin(u)./(N.*sin(u./N)));
subplot(2,2,1); plot(v,Fm); title 'F, вісь СВ '
axis([va vb 0 1.2]);grid on; hold on;
xlabel('v'); ylabel('Fm '); title (' Fm ');
Видно, що використавши звужений діапазон огляду кута Ɵ досить просто визначити будь-яке мале значення ШГП. В зв'язку з тим, що використані нормовані ДС за напруженістю поля , тому визначення ШГП здійснювалось за рівнем 0.7 та становить (96.4-83.6)=12.8, град.
Комбіновані ДС в сферичній системі . Комбінована ДС вказує на її неперервну залежність від одного з параметрів (script-файл s5n3, Додаток 5.3). .
Рис.5.23. Комбінована (при hn=0, N=2, в сферичній системі) ДС Fm (вікно 1) та її перерізи при dn1=1, dn2=0. 7, dn3=0. 5 (вікно 2); проекція одного з перерізів (dn4=0. 8) на площину ХOZ (вікно 3) .
Видно, що комбіновані ДС в сферичній системі (рис.5.23) являються більш інформативними, порівняно з ДС на площині (рис.5.7 – рис.5.16): вони надають інформацію про неперервну графічну залежність, в даному випадку, Fm(dn). Саме така інформація про неперервну графічну залежність ДС від одного з параметрів являється беззаперечною перевагою комбінованих ДС.
Комбіновані ДС в сферичній системі . Аналогічно можна використовувати (script-файл s5n4, Додаток 5.3) комбіновані ДС в прямокутній формі та її перерізи при Ɵ=const.
Рис.5.24. Комбінована (при hn=0, N=4, в прямокутній системі) ДС Fm (вікно 1) та її перерізи при Ɵ1=-90о, Ɵ2=0о, Ɵ3=45о (вікно 2) .
Такі ДС також вказують на неперервну залежність множника АР від значення dn.
Приведені ДС отримані на основі лістингу p5n2
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Основні показники досліджень множника АР полягають в наступному
а) б)
Рис. 5.21. Основні показники АР : а) частина 1; б) частина 2.
Таким чином проведена перша частина дослідження множника АР. Але також представляють інтерес інші його показники, зокрема визначення ШГП.