1.4.3. Картографічне представлення

Просторові ДС в прямокутній системі та картографічні ДС. Картографічне представлення ДС на площині може дати більш повну уяву про характер зміни ДС порівняно з звичайними ДС на площині. Для цього попередньо:

• формують просторову ДС в прямокутній системі;

• отримують на ній лінії однакового рівня ( які можна отримати, наприклад, шляхом перетину ДС площиною, для якої F(v)=Fa=const,

причому таких площин можна нанести багато

figure ('Color','w'); Ln=0.5;a=20;

for k=[1:3];

if k==1; Fa=0.3;

elseif k==2; Fa=0.5;

else Fa=0.7;

end

va=0;vb=360; vba=vb-va;

subplot(2,3,k);[v,g ]=meshgrid(va:vba/a:vb, va:vba/a:vb);

b1=2*pi*Ln;b2=cos(b1);b3=cos(b1.*cos(v.*pi/180))-b2;b4=(1-b2).*sin(v.*pi/180);

F=(g+1)./(g+1).*(abs(b3./b4)); surf(v,g,F);hold on;

Fd=Fa*(v+1)./(v+1).*(g+1)./(g+1); surf(v,g,Fd);

xlabel('v');ylabel('g ');

zlabel('F(v)');axis([0 360 0 360 0 1.2]);

end

subplot(2,3,1);title('ДС, площина F(v)=0.3');

subplot(2,3,2);title('ДС, площина F(v)=0.5');

subplot(2,3,3);title('ДС, площина F(v)=0.7');

Рис.1.36. ДС |F(v)| для СВ при Ln =0.5 в прямокутній системі, з допоміжною площиною F(v)=const

Далі здійснюється проекція отриманих перерізів на площину vOg, причому дані проекції формують картографічну ДС

figure ('Color','w'); Ln=0.5;a=200;

va=0;vb=180; vba=vb-va;

subplot(2,1,1);[v,g ]=meshgrid(va:vba/a:vb, va:vba/a:vb);

b1=2*pi*Ln;b2=cos(b1);b3=cos(b1.*cos(v.*pi/180))-b2;b4=(1-b2).*sin(v.*pi/180);

F=abs(b3./b4); [C,h] = contour(v,g,F);

set(h,'ShowText','on','TextStep',get(h,'LevelStep')*0.7);box off

colormap cool

Рис.1.37. Картографічна ДС (Fv) СВ при Ln =0.5

Варто зауважити, що в даному випадку отримано проекції перерізів на рівні 0.1k (k=1…10), причому використовуючи перерізи на рівні 0.7 можна визначити ШГП (2v_0.5)

Картографічні ДС на основі комбінованих ДС. Ще однією перевагою комбінованих ДС є створення на їх базі картографічних ДС. Спочатку, аналогічно (рис.1.35,б), здійснюється перетин комбінованої ДС декількома площинами при F(v)=const. Далі, аналогічно рис.1.37, здійснюється побудова картографічних ДС

figure ('Color','w');

a=20;Lna=0.01;Lnb=0.7;va=0;vb=180;vba=vb-va;Lba=Lnb-Lna;

subplot(2,1,1);[v,Ln ]=meshgrid(va:vba/a:vb, Lna:Lba/a:Lnb);

b1=2*pi*Ln;b2=cos(b1);b3=cos(b1.*cos(v.*pi/180))-b2;b4=(1-b2).*sin(v.*pi/180);

F=abs(b3./b4);[C,h] = contour(v,Ln,F);

set(h,'ShowText','on','TextStep',get(h,'LevelStep')*0.35);box off

colormap cool

xlabel('v');ylabel('Ln ');zlabel('F(v)');axis([va vb 0 0.7 0 1.2]);

Рис.1.38. Картографічна ДС (Fv) СВ на основі комбінованої ДС в прямокутній системі.

Приведена залежність є унікальною – вона дозволяє відслідкувати зміну ШГП на різних рівнях (від 0.1 до 0.9 з кроком 0.1) від максимального значення нормованої напруженості поля в залежності від довжини Ln для СВ. Нижче приведена аналогічна залежність на різних рівнях (від 0.1 до 0.9 з кроком 0.1) від максимального значення нормованої потужності поля

figure ('Color','w');

a=20;Lna=0.01;Lnb=0.7;va=0;vb=180;vba=vb-va;Lba=Lnb-Lna;

subplot(2,1,1);[v,Ln ]=meshgrid(va:vba/a:vb, Lna:Lba/a:Lnb);

b1=2*pi*Ln;b2=cos(b1);b3=cos(b1.*cos(v.*pi/180))-b2;b4=(1-b2).*sin(v.*pi/180);

F=abs(b3./b4);[C,h] = contour(v,Ln,F.^2);

set(h,'ShowText','on','TextStep',get(h,'LevelStep')*0.5);box off

colormap cool

xlabel('v');ylabel('Ln ');zlabel('F(v)');axis([va vb 0 0.7 0 1.2]);

Рис.1.39. Картографічна ДС ( F²(v) ) СВ на основі комбінованої ДС в прямокутній системі.

ДС (рис.1.39) більш зручні для користування (порівняно з ДС рис.1.38), тому що ШГП відраховується в рівнях (0.1, 0.5 і т.д) саме від максимального рівня кутової густини потужності.

5. Фазова діаграма спрямованості та поляризаційний вектор

Фазова діаграма. Як видно з залежності (1.2) комплексний вектор ДС, крім детально розглянутої амплітудної ДС, також містить фазову ДС. Таким чином, фазова ДС визначається, практично, аналогічно як і амплітудна ДС: це залежність фази ψ(v,g) напруженості поля в рівновіддалених від антени точках від кутів v, g сферичної системи координат.

Очевидно, що фаза поля на віддалі r від початку координат становить ψ(v,g) – kr= ψ_о . Для поверхні, де фаза фаза незмінна та становить ψ_о , повинна виконуватись умова

r(v,g)=[(ψ(v,g) –ψ_о]/k (1.8)

Якщо на антені існує така точка (фазовий центр), при розміщені якої в початку координат виконується умова ψ(v,g)=const , то r(v,g) – поверхня сфери. В даному випадку антена формує фронт хвилі у виді сфери, тобто антена випромінює сферичні хвилі.

Поляризаційний вектор. Комплексний вектор (1.2) також містить поляризаційний вектор. При розгляді поляризаційних характеристик використовують поняття площини поляризації, яка залежить від напрямку поширення хвиль та вектора напруженості електричного поля. Якщо даний вектор не змінює свого положення в просторі, то наявні лінійно-поляризовані хвилі, в іншому випадку –наявні хвилі з обертовою поляризацією, або еліптичною.

У випадку наземного зв’язку використовують поняття як вертикально- поляризованих хвиль, так і горизонтально- поляризованих.

Вертикальні лінійно-поляризовані хвилі. Для даних хвиль площина поляризації вертикальна до поверхні землі

figure ('Color','w');

for k=[1 2];

subplot(2,2,k);

a=15;xa=1;xb=3; xba=xb-xa;

[x,z ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);

surf(x-1,x./x.*z./z,z-1);hold on;

xlabel('x'); ylabel('y ');zlabel('z ');

axis([0 2.2 0 2.2 0 2.2]);

title('напрям поширення хвилі ');

end

subplot(2,2,2); [x,y ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);

T=1;w=2*pi/T; z=0.5*cos(w.*x);

surf(x-1,x./x.*y./y,z+1,'LineWidth',2);hold on;

а) б) х на t

Рис. 1.40. Вертикально-поляризовані хвилі: можливі орієнтації вектора поля (а); миттєві значення напруженості електричного поля (б)

Видно, що площина поляризації перпендикулярна до поверхні землі. Вектор електричного поля повинен бути розміщений в даній площині, але не обов’язково бути нормальним до поверхні землі. Миттєве значення напруженості поля становить

e_v=Evcos(wt) (1.9)

де Ev-амплітуда напруженості поля у вертикальній площині; w=2π/Т - кругова частота; Т – період коливань.

Горизонтальні лінійно-поляризовані хвилі. Для даних хвиль вектор електричного поля повинен бути паралельним до поверхні землі

figure ('Color','w');

for k=[1 2];

subplot(2,2,k);

a=15;xa=1;xb=3; xba=xb-xa;

[x,y ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);

surf(x-1,y-1,x./x.*y./y);hold on;

xlabel('x'); ylabel('y ');zlabel('z ');

axis([0 2.2 0 2.2 0 2.2]);

title('напрям поширення хвилі ');

end

subplot(2,2,2); [x,z ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);

T=1;w=2*pi/T; y=0.5*cos(w.*x);

surf(x-1,y+1,x./x.*y./y,'LineWidth',2);hold on;

а) б) х на t

Рис. 1.41. Горизонтально-поляризовані хвилі: можливі орієнтації вектора поля (а); миттєві значення напруженості електричного поля (б)

Видно, що можливі орієнтації вектора поляризації паралельні до поверхні землі. Можливі випадки коли площина поляризації не паралельна поверхні землі, але для горизонтально-поляризованої хвилі вектор поляризації повинен залишатись паралельним поверхні землі. Миттєве значення напруженості поля для горизонтально- поляризованих хвиль становить

e_g=E_gcos(wt +ψ) (1.10)

де E_g-амплітуда напруженості поля у горизонтальній площині; ψ – зсув фаз між векторами напруженості поля у вертикальній та горизонтальній площині.

Еліптична поляризація. Таку поляризацію можна розглядати як результат інтерференції двох лінійно-поляризованих хвиль (рис.1.40 , рис.1.41) в яких площини поляризації взаємно перпендикулярні. Коливання обох хвиль (1.9), (1.10) одинакові за частотою, але (обов’язково) зсунуті за фазою

figure ('Color','w');

for k=[1 ];

subplot(2,3,k);

a=15;xa=1;xb=3; xba=xb-xa;

[x,z ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);

surf(x-1,x./x.*z./z-1,z-2);hold on;

xlabel('t'); ylabel('y ');zlabel('z ');

axis([0 2.2 -1.2 1.2 -1.2 1.2]);

title('напрям поширення хвилі ');

end

for k=[ 1 3];

subplot(2,3,k); [x,y ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);

T=1;w=2*pi/T; z=0.8*cos(w.*x);

surf(x-1,x./x.*y./y-1,z,'LineWidth',2);hold on;

xlabel('t'); ylabel('y ');zlabel('z ');

axis([0 2.2 -1.2 1.2 -1.2 1.2]);

end

for k=[ 2];

subplot(2,3,k);

a=15;xa=1;xb=3; xba=xb-xa;

[x,y ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);

surf(x-1,y-2,x./x.*y./y-1);hold on;

xlabel('t'); ylabel('y ');zlabel('z ');

axis([0 2.2 -1.2 1.2 -1.2 1.2]);

title('напрям поширення хвилі ');

end

for k=[ 2 3];

subplot(2,3,k); [x,z ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb); q=pi/4

T=1;w=2*pi/T; y=0.4*cos(w.*x+q);

surf(x-1,y,x./x.*y./y-1,'LineWidth',2);hold on;

xlabel('t'); ylabel('y ');zlabel('z ');

axis([0 2.2 -1.2 1.2 -1.2 1.2]);

end

а) б) в)

Рис. 1.43. Вертикально-поляризована (а) та горизонтально- поляризована (б) хвилі, їх інтерференція (в)

Нижче приведено більш детальний приклад формування хвиль з еліптичною поляризацією в результаті інтерференції хвиль (рис.1.43,в)

figure ('Color','w');

for k=[1 2]

subplot(2,2,k);

a=15;xa=0;xb=2; xba=xb-xa;

[x,z ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);

surf(x,x./x.*z./z-1,z-1);hold on;

xlabel('t'); ylabel('Eg ');zlabel('Ev ');

axis([0 2.2 -1.2 1.2 -1.2 1.2]);

end

for k=[1 2 ]

subplot(2,2,k);

a=15;xa=0;xb=2; xba=xb-xa;

[x,y ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);

surf(x,y-1,x./x.*y./y-1);hold on;

xlabel('t'); ylabel('Eg ');zlabel('Ev ');

axis([0 2.2 -1.2 1.2 -1.2 1.2]);

end

for k=[1 2]

subplot(2,2,k);

a=15;xa=0;xb=2; xba=xb-xa;

[x,y ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);

surf(x,y-1,0.5*y.*x./x-0.5);hold on;

xlabel('t'); ylabel('Eg ');zlabel('Ev ');

axis([0 2.2 -1.2 1.2 -1.2 1.2]);

end

subplot(2,2,1);title('площина обертової поляризації');

subplot(2,2,2);title('площина обертової поляризації');

Рис. 1.44. Формування поляризаційного вектора

В кожен момент часу вектори Eg(t), Ev(t) характеризуються певним значенням модуля та фази, причому їх сума Ер(t)=Eg(t)+ Ev(t) формує поляризаційний вектор. Площина розміщення вектора Ер(t) (площина обертової поляризації) за один період ВЧ коливання здійснює повертання на кут 2π

йййййййййййййййййй

а) б)

в) г)

Рис. 1.45. Хвилі з еліптичною поляризацією за період ВЧ коливань: Ev(t) при Ev=1 та ψv=0 (а); Eg(t) при Eg=0.5 ψg=π/4 (б); просторова орієнтація кінця вектора Ер(t)= Ev(t)+ Eg(t) (в); область зміни поляризаційного вектора Ep (г)

Видно, що площина розміщення поляризаційного вектора нормальна до напрямку поширення хвиль, але постійно змінює свою орієнтацію відносно векторів Ev, Eg

Напрям обертання поляризаційного еліпса. Нижче приведено дані про еліптичну поляризацію аналогічні (рис.1.45), але за частину періода високочастотних коливань

figure ('Color','w');

for k=[ 1:4];

subplot(2,2,k);

a=150;xa=0;xb=1.3; xba=xb-xa;t=xa:xba/a:xb;q=pi/4;

T=2;w=2*pi/T; z1=1*cos(w.*t);y1=0.5*cos(w.*t+q);

plot3(t,y1,z1,'LineWidth',2);hold on;

xlabel('t');ylabel('Eg');zlabel('Ev');

grid on;axis([0 2.2 -1.2 1.2 -1.2 1.2]);

end

subplot(2,2,3); x=0; y=0;z=0;stem3(x,y,z,'fill');

subplot(2,2,4); x=0; y=0;z=0;stem3(x,y,z,'fill');

subplot(2,2,1);title('Ev(t)'); subplot(2,2,2);title('Eg(t)');

subplot(2,2,3);title('Ev(t)+Eg(t)'); subplot(2,2,4);title('Ev+Eg');

Рис. 1.46. Хвилі з еліптичною поляризацією за період ВЧ коливань: Ev(t) при Ev=1 та ψv=0 (а); Eg(t) при Eg=0.5 ψg=π/4 (б); просторова орієнтація кінця вектора Ер(t)= Ev(t)+ Eg(t) (в); область зміни поляризаційного вектора Ep (г)

Видно, що в даному випадку площина поляризації здійснила лише частину повного повертання. Таке повертання здійснювалось проти годинникової стрілки (вліво) при поширенні хвилі від передавача – тому вважається лівим напрямом обертання.

Але коливання е_g (1.10) може відставати за фазою від коливання е_v (1.9)

figure ('Color','w');

for k=[ 1:4];

subplot(2,2,k);

a=150;xa=0;xb=1.3; xba=xb-xa;t=xa:xba/a:xb;q=-pi/4;

T=2;w=2*pi/T; z1=1*cos(w.*t);y1=0.5*cos(w.*t+q);

plot3(t,y1,z1,'LineWidth',2);hold on;

xlabel('t');ylabel('Eg');zlabel('Ev');

grid on;axis([0 2.2 -1.2 1.2 -1.2 1.2]);

end

subplot(2,2,3); x=0; y=0;z=0;stem3(x,y,z,'fill');

subplot(2,2,4); x=0; y=0;z=0;stem3(x,y,z,'fill');

subplot(2,2,1);title('Ev(t)'); subplot(2,2,2);title('Eg(t)');

subplot(2,2,3);title('Ev(t)+Eg(t)'); subplot(2,2,4);title('Ev+Eg');

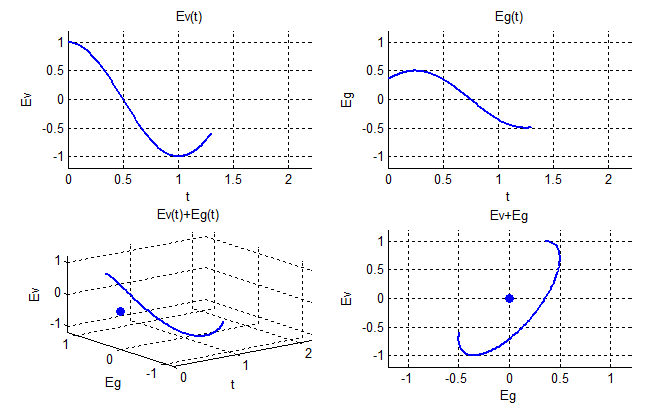
Рис. 1.47. Хвилі з еліптичною поляризацією за період ВЧ коливань: Ev(t) при Ev=1 та ψv=0 (а); Eg(t) при Eg=0.5 ψg=-π/4 (б); просторова орієнтація кінця вектора Ер(t)= Ev(t)+ Eg(t) (в); область зміни поляризаційного вектора Ep (г)

В даному випадку повертання поляризаційного вектора здійснювалось за годинниковою стрілкою (вправо) при поширенні хвилі від передавача – тому вважається правим напрямом обертання.

Вплив зсуву фаз.

figure ('Color','w');

for k=[ 1:4];

subplot(2,4,k);

a=150;xa=0;xb=2; xba=xb-xa;t=xa:xba/a:xb;q=pi/2;

T=2;w=2*pi/T; z1=1*cos(w.*t);y1=0.5*cos(w.*t+q);

plot3(t,y1,z1,'LineWidth',2);hold on;

xlabel('t');ylabel('Eg');zlabel('Ev');

grid on;axis([0 2.2 -1.2 1.2 -1.2 1.2]);

end

subplot(2,4,3); x=0; y=0;z=0;stem3(x,y,z,'fill');

subplot(2,4,4); x=0; y=0;z=0;stem3(x,y,z,'fill');

subplot(2,4,1);title('Ev(t)'); subplot(2,4,2);title('Eg(t)');

subplot(2,4,3);title('Ev(t)+Eg(t)'); subplot(2,4,4);title('Ev+Eg');

Рис. 1.47. Хвилі з еліптичною поляризацією за період ВЧ коливань: Ev(t) при Ev=1 та ψv=0 (а); Eg(t) при Eg=0.5 ψg=π/2 (б); просторова орієнтація кінця вектора Ер(t)= Ev(t)+ Eg(t) (в); область зміни поляризаційного вектора Ep (г)

figure ('Color','w');

for k=[ 1:4];

subplot(2,4,k);

a=150;xa=0;xb=2; xba=xb-xa;t=xa:xba/a:xb;q=0;

T=2;w=2*pi/T; z1=1*cos(w.*t);y1=0.5*cos(w.*t+q);

plot3(t,y1,z1,'LineWidth',2);hold on;

xlabel('t');ylabel('Eg');zlabel('Ev');

grid on;axis([0 2.2 -1.2 1.2 -1.2 1.2]);

end

subplot(2,4,3); x=0; y=0;z=0;stem3(x,y,z,'fill');

subplot(2,4,4); x=0; y=0;z=0;stem3(x,y,z,'fill');

subplot(2,4,1);title('Ev(t)'); subplot(2,4,2);title('Eg(t)');

subplot(2,4,3);title('Ev(t)+Eg(t)'); subplot(2,4,4);title('Ev+Eg');

Рис. 1.47. Хвилі з еліптичною поляризацією за період ВЧ коливань: Ev(t) при Ev=1 та ψv=0 (а); Eg(t) при Eg=0.5 ψg=0 (б); просторова орієнтація кінця вектора Ер(t)= Ev(t)+ Eg(t) (в); область зміни поляризаційного вектора Ep (г)

Вплив співвідношення амплітуд

figure ('Color','w');

for k=[ 1:4];

subplot(2,4,k);

a=150;xa=0;xb=2; xba=xb-xa;t=xa:xba/a:xb;q=pi/4;

T=2;w=2*pi/T; z1=1*cos(w.*t);y1=0.25*cos(w.*t+q);

plot3(t,y1,z1,'LineWidth',2);hold on;

xlabel('t');ylabel('Eg');zlabel('Ev');

grid on;axis([0 2.2 -1.2 1.2 -1.2 1.2]);

end

subplot(2,4,3); x=0; y=0;z=0;stem3(x,y,z,'fill');

subplot(2,4,4); x=0; y=0;z=0;stem3(x,y,z,'fill');

subplot(2,4,1);title('Ev(t)'); subplot(2,4,2);title('Eg(t)');

subplot(2,4,3);title('Ev(t)+Eg(t)'); subplot(2,4,4);title('Ev+Eg');

Рис. 1.47. Хвилі з еліптичною поляризацією за період ВЧ коливань: Ev(t) при Ev=1 та ψv=0 (а); Eg(t) при Eg=0.5 ψg=0 (б); просторова орієнтація кінця вектора Ер(t)= Ev(t)+ Eg(t) (в); область зміни поляризаційного вектора Ep (г)

figure ('Color','w');

for k=[ 1:4];

subplot(2,4,k);

a=150;xa=0;xb=2; xba=xb-xa;t=xa:xba/a:xb;q=pi/4;

T=2;w=2*pi/T; z1=1*cos(w.*t);y1=1*cos(w.*t+q);

plot3(t,y1,z1,'LineWidth',2);hold on;

xlabel('t');ylabel('Eg');zlabel('Ev');

grid on;axis([0 2.2 -1.2 1.2 -1.2 1.2]);

end

subplot(2,4,3); x=0; y=0;z=0;stem3(x,y,z,'fill');

subplot(2,4,4); x=0; y=0;z=0;stem3(x,y,z,'fill');

subplot(2,4,1);title('Ev(t)'); subplot(2,4,2);title('Eg(t)');

subplot(2,4,3);title('Ev(t)+Eg(t)'); subplot(2,4,4);title('Ev+Eg');

Колова поляризація.

figure ('Color','w');

for k=[ 1:4];

subplot(2,4,k);

a=150;xa=0;xb=2; xba=xb-xa;t=xa:xba/a:xb;q=pi/2;

T=2;w=2*pi/T; z1=1*cos(w.*t);y1=1*cos(w.*t+q);

plot3(t,y1,z1,'LineWidth',2);hold on;

xlabel('t');ylabel('Eg');zlabel('Ev');

grid on;axis([0 2.2 -1.2 1.2 -1.2 1.2]);

end

subplot(2,4,3); x=0; y=0;z=0;stem3(x,y,z,'fill');

subplot(2,4,4); x=0; y=0;z=0;stem3(x,y,z,'fill');

subplot(2,4,1);title('Ev(t)'); subplot(2,4,2);title('Eg(t)');

subplot(2,4,3);title('Ev(t)+Eg(t)'); subplot(2,4,4);title('Ev+Eg');

%%%%%%%%%%%%%%%%%%%%%%%

Висновки

1.

2.

3.

Контрольні питання

1. Що таке амплітудна ДС передавальних антен.

2. Як треба розмістити СВ для забезпечення наземного зв’язку. Привести ДС в полярній системі, яка підтверджує необхідність такого розміщення.

3. Що таке довжина хвилі. Визначити довжину хвилі для частоти 300 мГц.

4. Від чого залежить ДС СВ . Привести ДС в полярній системі для різних випадків

5. Як визначити ШГП антени на базі графічного представлення ДС

6. Як визначити КСД антени на базі графічного представлення ДС 7.

7. Класифікація антен

8. Картографічні ДС та їх визначення

9. Аналітичні залежності ( не нормовані та нормовані) для ДС ІА, СВ, ДГ, ЕГ.

Вимоги згідно Політехніки +1

Список скорочень +1

Поправити рисунки та формули +1

10 питань до розділу +1

Роздукувати розділ+1

Свої пропозиції +2

Пропущені очевидні помилки -10

Сам повине вміти пояснити (крім програм) описаний матеріал – питання до заліку

Зміст

Список літератури