1.4. Діаграма спрямованості елементарних випромінювачів
Як показано вище, форма ДС антени має велике значення при її виборі для кожного конкретного випадку. В загальному випадку ДС антени можна визначити використовуючи закони електродинаміки, що є досить складною задачею. І в вирішенні даної проблеми неоціненну допомогу надають елементарні випромінювачі, які дозволяють значно спростити визначення ДС конкретних антен.
Загальні відомості. Елементарні випромінювачі (в чистому виді) неможливо виготовити практично. Але антени з неперервним розподілом поля можна розглядати, як нескінченну сукупність елементарних випромінювачів
а) б)
Рис.1.8. Антени з неперервним розподілом поля, як сукупність нескінченної кількості елементарних випромінювачів: лінійні (а); апертурні (б)
Приведені результати отримані на основі наступного фрагменту програми
figure ('Color','w');
subplot(2,2,1);
x=[0:0.1:1]; y=x./x-1;
plot(x,y,'--rs','LineWidth',2,...
'MarkerEdgeColor','k',...
'MarkerFaceColor','g',...
'MarkerSize',10)
axis([0 1.2 0 1.2]); axis off ;
subplot(2,2,2);
x=[0:0.1:1]; y=x./x-1;
for k=[0:5]
plot(x,y+k/10,'--rs','LineWidth',2,...
'MarkerEdgeColor','k',...
'MarkerFaceColor','g',...
'MarkerSize',10); hold on;
end
axis([0 1.2 0 1.2]); axis off ;
В лінійних антенах розмір поперечного перерізу значно менший за довжину хвилі. Виготовляються лінійні антени з провідників, або у вигляді щілин у металічних поверхнях. Кожному з вказаних типів лінійних антен відповідає свій елементарний випромінювач: для провідників – електричний диполь (диполь Герца) ; для щілин – елементарний щілинний випромінювач.
В апертурних антенах випромінювання відбувається через певну уявну поверхню, яка розділяє внутрішній об’єм антени та зовнішній простір. Така поверхня є апертурою або розкривом та переважно представляє собою площину. І для апертурних антен також наявний елементарний випромінювач – елемент Гюйгенса.
Отже, будь-яку реальну антену можна розглядати як сукупність великої кількості елементарних випромінювачів. Далі на основі ДС елементарних випромінювачів ( яка визначається відносно просто) можна визначити ДС реальної антени. В цьому і полягає основна цінність елементарних випромінювачів.
Диполь Герца. Він являє собою випромінювач, що складається з відрізкa провідника довжиною Ld та максимальним розміром поперечного перерізу Sd
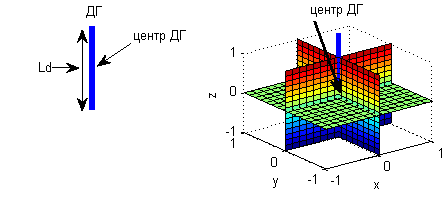
а) б)
Рис. 1.9. Диполь Герца: будова (а); розміщення при визначенні ДС (б)
Приведені результати отримані на основі наступного фрагменту програми
figure ('Color','w');
subplot(2,2,1); t = 1:0.01:2.4; plot(t./t-1,t-1.2,'LineWidth',4 );
axis([-1.2 1.2 -1.2 1.2]);title(' ДГ '); axis off
a=15;
xa=1;xb=3; xba=xb-xa;
xa=1;xb=3; xba=xb-xa;
[x,y ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);
subplot(2,2,2);surf(x-2,y-2,x./x.*y./y-1);hold on;
[y,z ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);
surf(y./y.*z./z-1,y-2,z-2);hold on;
[x,z ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);
surf(x-2,x./x.*z./z-1,z-2);
t = 1:0.01:2.4; plot3(t./t-1,t./t-1,t-0.8,'LineWidth',3 );hold on;
xlabel('x'); ylabel('y ');zlabel('z ');
axis([-1.0 1.0 -1.0 1.0 -1.0 1.0]); title('центр ДГ');
%%%%%%%%%%%%%%%%%%%%%%%%%%
Віссю антен є одна (унікальна) пряма, що залежить від їх будови. Для ДГ віссю є пряма, що проходить вздовж його довжини. Отже, при визначенні ДС ДГ його вісь розміщується вздовж осі OZ, а середина (центр) ДГ –в початку осей координат.
Для ДГ повинні виконуватись три наступні умови
довжина провідника Ld набагато менша за довжину хвилі (Ld‹‹λ);
максимальний розмір поперечного перерізу також набагато менший за довжину хвилі (Ld‹‹λ);
амплітуда струму одинакова вздовж його довжини (Id=const).
Очевидно, що реалізувати диполь Герца в «чистому» виді практично неможливо, тому що струм на кінцях провідника, згідно з законами збереження електрики, повинен бути рівним нулю.
Діаграма спрямованості. Як показано в Додатку 1.3 амплітуда напруженості електричного поля диполя Герца на значній віддалі r ( набагато більшій за його максимальні розміри та довжину хвиилі) визначається наступним чином
Е=nd sin(v) (3.1)
де nd=30kIdLd/r, k=2π/λ
Отже амплітудна ДС (як лише та складова, що залежить від кутів сферичної системи – в даному випадку тільки від кута v) становить sin(v), максимальне значення якої становить одиницю. В результаті отримаємо (дуже рідкий випадок) , що для диполя Герца амплітудна ДС та її нормоване значення рівні між собою
f(v) =F(v) = sin (v) – ДС за напруженістю поля (3.2,а)
fр(v) =Fр(v) = sin2 (v) – ДС за потужністю (3.2,б)
Видно, що форму ДС ДГ неможливо змінити – вона не залежить від його геометричних розмірів. Графічне представлення отриманих ДС у виді просторових залежностей надає найбільш повну та наочну інформацію про характер випромінювання ДГ
figure ('Color','w');
for k= [ 1 2 3 ]
if k==1; gn=-pi/2 ; gv=pi;a=15;
elseif k==2; gn=0; gv=0.01*pi; a=150;
else gn=0; gv=0.01*pi;a=150;
end
subplot(2,3,k);
gvn=gv-gn; vn=0; vv=pi;vvn=vv-vn;
[g, v]=meshgrid(gn:gvn/a:gv, vn:vvn/a:vv);
F=abs(sin(v));x=F.*sin(v).*cos(g); y=F.*sin(v).*sin(g);
z=F.*cos(v).*(g+1)./(g+1);surf(x,y,z);hold on;
t = 0:0.01:2.4; plot3(t./t-1,t./t-1,t-1.2,'LineWidth',2 );
xlabel('x'); ylabel('y ');zlabel('z ');hold on;
axis([-1.2 1.2 -1.2 1.2 -1.2 1.2]);
end
for k= [ 2 3 ];
subplot(2,3,k);
gn=pi ; gv=gn+0.01*pi;gvn=gv-gn; vn=0; vv=pi;vvn=vv-vn; a=150;
[g, v]=meshgrid(gn:gvn/a:gv, vn:vvn/a:vv);
F=abs(sin(v));x=F.*sin(v).*cos(g); y=F.*sin(v).*sin(g);
z=F.*cos(v).*(g+1)./(g+1);surf(x,y,z);hold on;
xlabel('x'); ylabel('y ');zlabel('z ');hold on;
axis([-1.2 1.2 -1.2 1.2 -1.2 1.2]);
end
subplot(2,3,3); a=150;
[g, v]=meshgrid(0:pi/a:pi/a, 0:pi/a:2*pi);F=1;
x=F.*sin(v).*cos(g); y=F.*sin(v).*sin(g); z=F.*cos(v).*(g+1)./(g+1);
surf(x,y,z,'LineWidth',2);hold on;
xlabel('x'); ylabel('y ');zlabel('z '); axis([-1.2 1.2 -1.2 1.2 -1.2 1.2]);
subplot(2,3,1); title('ДС ДГ , вісь ДГ');
subplot(2,3,2); title('переріз в пл. XOZ ');
subplot(2,3,3); title('проекція перерізів: ДГ,ІА');
Рис.3.3. Просторова ДС ДГ в сферичній системі (нормована та ненормована) за напруженістю поля
Видно, що просторова ДС ДГ за напруженістю поля формується обертанням ДС (3.2,а) навколо його осі. Максимальне значення ДС ДГ рівне ДС ІА та становить 1.
%%%%%%%%%%%%%%%
Розміщення антен при аналізі. При аналізі антен, з метою визначення аналітичних залежностей для ДС, їх центр розташовується в початку координат, а вісь – вздовж однієї з осей системи координат ( найчастіше вздовж осі OZ). Розглянемо, наприклад, розташування симетричного вібратора (СВ) при його аналізі
Рис. 1.8. СВ: будова (а); розміщення при визначенні ДС (б)
Приведені дані отримані на основі наступного фрагменту програми
figure ('Color','w');
subplot(2,2,1);
t = 0:0.01:4.0; plot(t./t-1,t-2.0,'LineWidth',1 );hold on;
t = 0:0.01:1.2; plot(t./t-1,t-1.3,'LineWidth',6 );hold on;
plot(t./t-1,t+0.1,'LineWidth',6 );hold on;
axis([-1.2 1.2 -2.2 2.2]);title(' СВ '); axis off
a=15; xa=1;xb=3; xba=xb-xa;
[x,y ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);
subplot(2,2,2);surf(x-2,y-2,x./x.*y./y-1);hold on;
[y,z ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);
surf(y./y.*z./z-1,y-2,z-2);hold on;
[x,z ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);
surf(x-2,x./x.*z./z-1,z-2);
t = 1:0.01:2.4; plot3(t./t-1,t./t-1,t-0.8,'LineWidth',3 );hold on;
xlabel('x'); ylabel('y ');zlabel('z ');
axis([-1.0 1.0 -1.0 1.0 -1.0 1.0]); title('центр CВ');
Видно, що СВ містить два плеча (довжиною L), розташованих вздовж однієї прямої – його осі. При визначенні ДС СВ його вісь розміщується вздовж осі OZ, а його середина – в початку координатних осей.
Для вказаного розміщення антен в результаті аналізу, проведеного в подальших розділах, отримано значення ДС деяких антен (табл. 1.2)
Значення ДС антен за напруженістю поля
Таблиця 1.2
|
Антена |
ДС (f) |
fмакс |
Нормована ДС |
|
ІА |
|
1 |
|
|
ДГ |
|
1 |
|
|
ЕГ |
|
2 |
|
|
СВ |
|
1-сos(2πLn) |
|
В формулах sin(v) а не sinv.
Саме на прикладі таких антен в даному розділі, буде проводитись дослідження ДС. Особливе місце серед вказаних антен займає ІА.
Ізотропна антена. Вона представляє собою точку, що розміщена в початку системи координат, причому її віссю може бути будь-яка пряма, що проходить через дану точку. ІА забезпечує одинакову інтенсивність випромінювання у всіх напрямках. Але неможливо побудувати строго ІА. Вона існує тільки в теорії та є ніби «еталоном», призначеним для порівняння з нею різноманітних реальних антен. Саме наявність результатів порівняння різних антен з «еталоном» дозволяє провести взаємне порівняння антен між собою. Ні одна реальна антена не здатна (та практично і не потрібна така антена) забезпечити однакову інтенсивність випромінювання у всіх напрямках.
Розміри антен та їх взаємозв’язок з довжиною хвилі. Розміри антен залежать від довжини хвилі, на якій вона повинна функціонувати. Довжина хвилі , тобто віддаль, яку проходить хвиля за час рівний періоду Т, визначається наступним чином
λ=сТ =с/f (1.6)
де с=3*108м/с –швидкість світла; f –частота коливань.
З залежності (1.6) видно, що довжині хвилі 1м відповідає частота 300 мГц, тобто вище частоти 300 мГц починаються дециметрові хвилі, вище частоти 3гГц – сантиметрові і т.д. В загальному випадку розміри антен повинні бути співрозмірні з довжиною хвилі високочастотних коливань, що використовуються в даній системі зв’язку.
Приклад одного з видів представлення амплітудних ДС. Нижче приведено приклад одного з видів графічного представлення ДС антен (згідно даних табл.1.2) - в полярній системі
figure ('Color','w'); Ln=0.625; v=[0:pi/115:2*pi];
subplot(2,3,1);
F=2*v./v;polar(v,F);hold on;
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=sin(v);
F=abs(b3./b4);polar(v,F);hold on;title('вісь СВ,Ln=0.625');
for k=[2:3];
if k==2; F=abs(sin(v));
else F=1+cos(v);
end
subplot(2,3,k);
F1=2*v./v;polar(v,F1);hold on;
polar(v,F);hold on;
end
subplot(2,3,2);title('вісь ДГ');subplot(2,3,3);title('вісь ЕГ');
Рис.1.9. ДС f(v) в полярній системі ( ДГ, ЕГ, СВ)
ДС для СВ (рис.1.9) отримана на основі програми 1.1
Програма 1.1.
figure ('Color','w'); Ln=0.625; v=[0:pi/115:2*pi];
subplot(2,3,1);
b1=2*pi*Ln; b2=cos(b1);b3=cos(b1.*cos(v))-b2;b4=sin(v);
F=abs(b3./b4);polar(v,F);hold on;title('вісь СВ,Ln=0.625');
Головна та бокові пелюстки ДС. В ДС антен може бути один або декілька напрямків максимального випромінювання (пелюсток). У випадку наявності декількох пелюсток, наприклад для СВ при Ln=0.625, розрізняють головну пелюстку (ГП, для якої максимальне випромінювання найбільше) та бокові (БП, для яких максимальне значення менше, порівняно з ГП).
Видно,що максимальні значення для ДС кожної антени різні. Для ДГ та СВ характерне двостороннє поперечне випромінювання (вздовж нормалі до їх осі), а для ЕГ – одностороннє поздовжне випромінювання (вздовж одного напрямку осі ЕГ). Для БП СВ характерне нахилене випромінювання.
Спрямованість антен. Для різних антен також характерна різна ширина ДС. Очевидно, що антени з меншою шириною ДС забезпечують більшу спрямованість, що в багатьох випадках є корисним. Так, наприклад антени з вузькою ДС дозволяють збільшувати напруженість поля в заданій стаціонарній точці приймання без збільшення потужності передавача, що економічно більш вигідно. Крім того, концентрація електромагнітних хвиль в необхідному напрямі приводить до зменшення взаємних перешкод різних радіотехнічних систем. Наявність приймальних антен з більш вузькою ДС веде до ослаблення прийому різних зовнішніх перешкод, тобто до підвищення якості приймання і поліпшення завадостійкості приймального пристрою. Значну спрямованість випромінювання повинні забезпечувати антени для космічного радіозв'язку, радіоастрономії, радіолокації, радіорелейних ліній. В той же час, для радіомовлення і телебачення передавальні антени повинні забезпечувати одинакове випромінювання в усіх напрямках вздовж земної поверхні (рис.1.7,а). Всі антени з точки зору оцінки випромінювання можна розбити на два основних класи:
випромінюючі енергію в значну частину простору (слабоспрямовані або неспрямовані антени);
концентруючі енергію в малому об’ємі (спрямовані антени).
Кількісно спрямованість антени характеризується , в основному, двома параметрами: коефіцієнтом спрямованої дії (КСД) та шириною ГП (ШГП).
Ширина головної пелюстки. ШГП визначається кутом (2v ) в межах ГП, в яких кутова густина потужності становить заданий рівень Sр по відношенню до максимального. Найбільш часто використовується значення Sр=0.5, яке відповідає половині потужності (при цьому ШГП позначається 2v0.5). Крім того, може визначатись ШГП (2v0.1 та 2v0) також при інших значеннях Sp (Sp=0.1 та Sp=0), які відповідають рівню 0.1 від максимального значення кутової густини потужності та нульовому рівню ГП, відповідно. Значення Sp застосовується при визначенні ШГП на основі амплітудних ДС, побудованих за кутовою густиною потужності поля.
У випадку використання для визначення ШГП амплітудних ДС, побудованих за напруженістю поля, необхідно використати значення SЕ=√Sp, тому що ДС за потужністю рівна квадрату напруженості ДС за напруженістю поля (табл..1.1). Отже, для визначення ШГП (2v0.5, 2v0.1 та 2v0) необхідно використовувати значення (SЕ=0.7, SЕ=0.32 та SЕ=0), відповідно.
Коефіцієнт спрямованої дії. Використовуючи ДС також можна орієнтовно визначити КСД антени
Do=(35 000…45 000)/[(2vo0.5)E(2vo0.5)H] (1.7)
де (2vo0.5)E , (2vo0.5)H - ШГП в головних площинах
Головними є взаємоперпендикулярні площини, які проходять через напрям максимального випромінювання антени. Нижче приведено, наприклад, головні площини для ЕГ
figure ('Color','w');
for k=[1:3]
subplot(2,3,k);
gn=0; gv=2*pi;gvn=gv-gn; vn=0; vv=pi;vvn=vv-vn; a=15;
[g, v]=meshgrid(gn:gvn/a:gv, vn:vvn/a:vv);
F=abs(1/2*(1+cos(v)));
x=F.*sin(v).*cos(g); y=F.*sin(v).*sin(g); z=F.*cos(v).*(g+1)./(g+1);
surf(x,y,z);hold on; xlabel('x'); ylabel('y ');zlabel('z ');hold on;
t = 0:0.01:2.4; plot3(t./t-1,t./t-1,t-1.2,'LineWidth',2 );hold on;
axis([-1.2 1.2 -1.2 1.2 -1.2 1.2]);title('вісь ЕГ');
end
subplot(2,3,3);
a=15; xa=1;xb=3; xba=xb-xa;
[y,z ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);surf(y./y.*z./z-1,y-2,z-2);hold on;
[x,z ]=meshgrid(xa:xba/a:xb, xa:xba/a:xb);surf(x-2,x./x.*z./z-1,z-2);
а) б) в)
Рис.1.10. ДС F(v) для ЕГ в сферичній системі: просторова (а); проекція на площину XOZ (б); з головними площинами (в)
Видно (рис.1.10,б), що максимальне значення ДС спрямоване вздовж осі ЕГ. Тому головні площини повинні проходити через вісь ЕГ та бути взаємноперпендикулярними.