1. Границя функції в точці.

Надалі, говорячи про границю функції y = f ( x)

в точці x0 , будемо вважати, що функція y = f ( x)

задана в деякому проколотому околі точки x0 .

f ( x) при x , що прямує

Означення 1 (Коші, на мові “ e - d ”). Число A називається границею функції

до x0 (або в точці x0 ), якщо для довільного числа

e > 0 існує таке

число d = d ( e )

> 0 , що для всіх

x Î D ( f ) , які задовольняють умову 0 <| x - x0 |< d , виконується нерівність | f ( x) - A |< e .

Якщо число A є границею функції f ( x) в точці x0

lim f (

x) = A

або

f ( x)

® A при x ® x0 .

, то пишуть x®x

0

Отже,

lim f ( x) = A

def

"e > 0

$d = d ( e ) > 0 "x Î D ( f ) : 0 <

x - x0

f (

x) - A

=

< d Þ

< e .

x®x

0

Суть означення границі функції

f ( x)

в точці x0

полягає в тому, що для всіх значень x , достатньо

близьких до x0 , значення функції

f ( x)

за абсолютною величиною як завгодно мало відрізняються від

числа A .

2x +1

Приклад. Користуючись означенням Коші границі функції в точці, довести, що lim

= -5 .

Розв’язання. Розглянемо функцію f ( x) = 2x + 1

x®2

x - 3

у деякому околі точки

x0 = 2 , який не містить точки

x - 3

2x +1

7

x - 2

x = 3 , наприклад, на інтервалі (1,5;2,5) . Тоді "x Î(1,5;2,5)

x - 3

> 0,5

і

+ 5

=

< 14

x - 2

.

x - 3

x - 3

1

Візьмемо довільне додатне число e . Якщо вибрати

d =

e

, то для всіх

x Î(1,5;2,5)

, які задовольняють

14

умову 0 <| x - 2 |< d , виконується нерівність

2x +1 + 5

< e . За означенням Коші число

A = -5 є границею

x - 3

функції f ( x) =

2x +1

в точці x0 = 2 .

x - 3

limsin x = 0

.

Вправа. Користуючись означенням Коші границі функції в точці, довести, що x®0

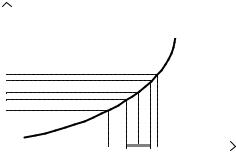
Геометричний зміст границі функції в точці. Число A є границею функції

f (

x) при x ® x0 , якщо

для довільного e > 0 знайдеться такий проколотий

d -окіл точки x0 , що для всіх

x Î( x0 - d ; x0 + d ) \ { x0 }

відповідні ординати точок графіка функції y = f ( x)

будуть міститися в смузі A - e < y < A + e , якою би

вузькою ця смуга не була (рис. 1).

A

+ e

A

A

- e

x 0

x

0

x 0 -

d

x

0 + d

Рис. 1. Графічна інтерпретація означення границі функції в точці

Означення 2 (Гейне, на мові послідовностей). Число

A називається границею функції f ( x) в точці

x0 , якщо "{ xn } такої, що xn ® x0 , xn Î D ( f ) ,

xn ¹ x0 виконується умова

lim f

(

x

n )

= A

.

n®¥