Вільні коливання підресореної маси

Використовуючи зведені жорсткості пружних елементів і нехтуючи непідресореними масами, можна одержати спрощену одномасову коливну систему автомобіля з двома ступенями вільності. Ця система дозволяє вертикальні переміщення zцентру підресореної маси і поворот її в поздовжній площині на кут α (рис. 79).

Рис. 79. Одномасова коливна модель автомобіля

Обидва ці рухи викликають прогини z₁іz₂пружних елементів і виникнення сил пружності;, що діють з боку пружних елементів на підресорену масу. Рівняння рівноваги сил, що діють вздовж осіz, та моментів відносно центру підресореної маси точки О мають вигляд:

В цих рівняннях – вертикальне прискорення центру маси;– кутове прискорення підресореної маси;– момент інерції підресореної маси відносно поперечної осіy;a_п,b_п– координати підресореної маси. З рис. 79 можна визначити, що, а оскільки для малих кутів, то можна вважати, що, і. Також з цього рисунка можна встановити, що, звідки. Після підставляння виразів дляірівняння рівноваги матимуть вигляд:

Після множення першого рівняння на а_пі віднімання його від другого, множення першого рівняння наb_пі додавання його до другого виходить система рівнянь

Після замін

;;;

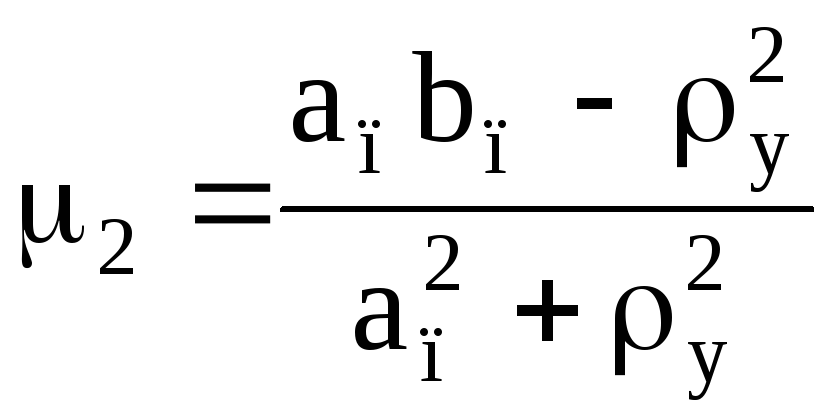система рівнянь, що описують вільні коливання підресореної маси, набуває вигляду

Результатом доволі складного розв'язку цієї системи рівнянь є два корені

Це означає, що коливання підресореної маси фактично є сумою двох коливань: низькочастотних з частотою Ω_ні високочастотних з частотою Ω_в.

Результуюча система рівнянь вважається зв’язаною, тому що у перше рівняння поряд з прискоренням і переміщеннямz₁точки А входить прискоренняточки В, а в друге рівняння входять як прискоренняі переміщенняz₂ точки В, так і прискоренняточки А. Тому коливання точок А і В пов’язані між собою. Це проявляється в тому, що коливання кожної з цих точок є сумою синусоїдних коливань з різними амплітудами і частотами, які залежать від параметрів своїх підвісок. Ці залежності визначаються коефіцієнтами зв’язку μ₁і μ₂, на які перемножуються прискоренняі. Чим більші значення цих коефіцієнтів, тим більший взаємний вплив параметрів задньої підвіски на коливання точки А і параметрів передньої підвіски на коливання точки В, а також більша різниця між частотами Ω_ні Ω_в. На значення коефіцієнтів μ₁і μ₂в основному впливає різниця. Відношенняназивається коефіцієнтом розподілу підресореної маси. Якщо, тоі обидва коефіцієнти зв’язку стають рівними нулю. В цьому разі система рівнянь, що описують коливання матиме вигляд

Рівняння стають незалежними одне від одного, отже незалежними стають і коливання точок А і В, тому можна вважати, що підресорена маса розпадається на дві незв’язані маси, одна з яких опирається на передню підвіску, інша – на задню.

Коефіцієнти, на які перемножуються амплітуди z₁іz₂– це квадрати частот власних коливань підресореної маси на передній і задній осях. Кожна з цих частот характеризує вільні коливання підресореної маси на одній пружній опорі, коли інша опора замінена нерухомим шарніром (рис. 5). Частоти цих коливань з одним ступенем вільності називаються парціальними.

Рис. 80. Схеми коливань підресореної маси з парціальними частотами ω₁ (а) та ω₂ (б)