1. Магнітне поле прямолінійного провідника зі струмом.

Р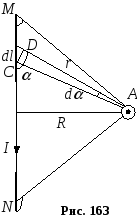озглянемопрямий провідникдовільної довжини, по якому проходить струм силоюІ, наприклад згори вниз (рис. 163). Відповідно до закону Біо-Са­вара-Лапласа вектор магнітної індукціїполя у вакуумі, створеного в точціАелементомпровідника зі струмом, числово дорівнює

,

де – кут між векторамиі.

У точці А, яка знаходиться на відстаніRвід осі провідника, всі вектори, які характеризують магнітні поля, створені окремими ділянками цього провідника, напрямлені перпендикулярно до площини рисунка. Векторчислово дорівнює алгебраїчній сумі модулів векторів:

.

Замінимо dlіrчерез одну незалежну змінну:

,,.

Тоді:

.

У результаті індукція магнітного поля прямолінійного провідника MNу точ­ціАдорівнює:

.

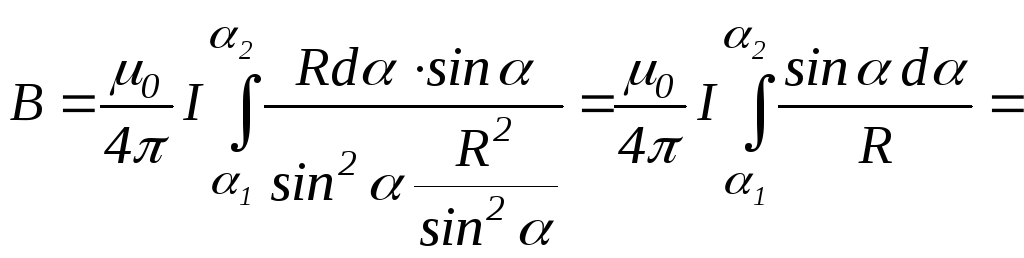
Якщо провідник МNнескінченно довгий, то, а.

Отже, магнітна індукція нескінченно довгого провідника зі струмом дорівнює ,

.

2. Магнітне поле колового струму.

Знайдемо індукцію магнітного поля в центрі О,колового струмурадіусомR,по якому протікає струмІ(рис. 164):

,

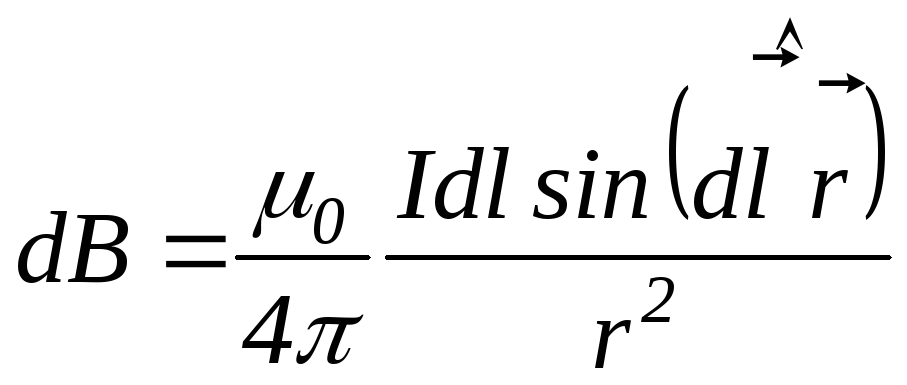
,r=R.

Тоді

.

Усі вектори магнітних полів, які створені в точціОрізними ділянкамиколового струму, напрямлені перпендикулярно до площини рисунка „від нас”. Тоді:

.

Отже, магнітна індукція поля колового струму дорівнює:

.

§67. Закон Ампера

На провідники зі струмом, що знаходяться в магнітному полі, діють сили Ампера.

Узагальнюючи результати дослідження дії магнітного поля на різні провідники зі струмом, Ампер встановив, що

сила , з якою магнітне поле діє на елемент довжинипровідника зі струмом, що знаходиться в магнітному полі, прямо пропорційна до сили струмув провіднику і до векторного добутку елемента довжинина магнітну індукцію:

.

Це співвідношення називається законом Ампера.

Напрямок сили можна знайти за правилом векторного добутку і за правилом лівої руки: якщо долоню лівої руки поставити так, щоб у неї входили лінії магнітної індукції, а чотири витягнуті пальці спрямувати в напрямку електричного струму в провіднику, то відставлений навеликий палець покаже напрямок сили, що діє на провідник з боку поля. Це правило зручне, коли елемент провідника зі струмом перпендикулярний до напрямку магнітного поля.

В загальному випадку для визначення напрямку сили Ампера слід скористатись правилом векторного добутку: векторнапрямлений перпендикулярно до площини, утвореної векторами ітак, щоб з кінця вектораобертання від векторадо векторанайкоротшим шляхом відбувалося проти годинникової стрілки (рис. 165).

Модуль сили Ампера розраховується за формулою

,

де  - кут між векторамиі.

Закон Ампера дає змогу визначити іншим способом, ніж раніше, фізичний зміст магнітної індукції .

Припустимо, що елемент провідника із струмомIперпендикулярний до напрямку магнітного поля, тоді закон Ампера можна записати у вигляді:

.

Звідси, магнітна індукція числово дорівнює силі, що діє з боку поля на одиницю довжини провідника, по якому протікає електричний струм одиничної сили і який розташовано перпендикулярно до напрямку магнітного поля.

Отже, магнітна індукція є силовою характеристикою магнітного поля.

Використовуючи закон Ампера, розраховуємо силу взаємодії між двома прямими нескінченно довгими провідниками зі струмами і, які розміщені паралельно один до одного на відстаніR. Кожен із провідників створює магнітне поле, яке діє згідно закону Ампера на другий провідник. Якщо електричні струми і однакового напрямку, то провідники притягуються один до одного (рис. 166а), а якщо напрямки струмів взаємно протилежні, то провідники відштовхуються один від одного (рис. 166б).

За законом Ампера на елемент провідника зі струмомдіє сила, яка числово дорівнює:

,

де - магнітна індукція поля, створеного струмом, враховуючи, що кут між векторамиі– прямий, отримуємо:

.

Відповідно на ділянку провідника зі струмомдіє сила, модуль якої:

.

Отже, для сил іможна написати загальну формулу:

.