§109. Квантова гіпотеза і формула Планка

В 1900 р. М.Планк вперше знайшов правильний вираз для функції Кірхгофа і обґрунтував спектральні закономірності випромінювання абсолютно чорного тіла.

В своїх розрахунках Планк, враховуючи, що об’ємна густина енергії рівноважного випромінювання в замкненій порожнині залежить від температури стінок порожнини, а матеріал стінок значення не має, вибрав найпростішу модель випромінювальної системи у вигляді сукупності лінійних гармонічних осциляторів (елек­тричних диполів) з найрізноманітнішими частотами . Кожний з таких осциляторів відповідає монохроматичній компоненті чорного випромінювання.

Нехай - середнє значення енергії осцилятора з власною частотою. Тоді випромінювальна здатність абсолютно чорного тіла

.

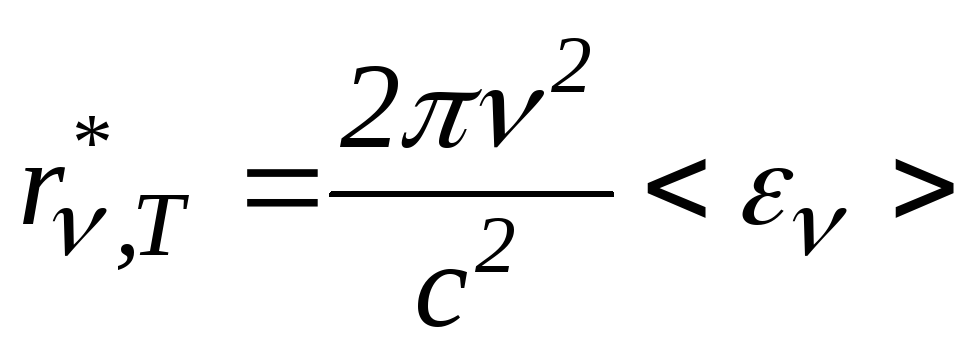Правильний вираз для середньої енергії осцилятора і функції Кірхгофа вдалось знайти Планку введеннямквантової гіпотези, яка зовсім не притаманна класичній фізиці. У класичній фізиці припускається, що енергія будь-якої системи може змінюватись неперервно, набираючи будь-яких, як завгодно близьких значень.

За квантовою гіпотезою Планка енергія осцилятора може набувати тільки певних дискретних значень, які дорівнюють цілому числу елементарних порцій - квантів енергії:

.

Вираз для Планк отримав в такому вигляді:

.

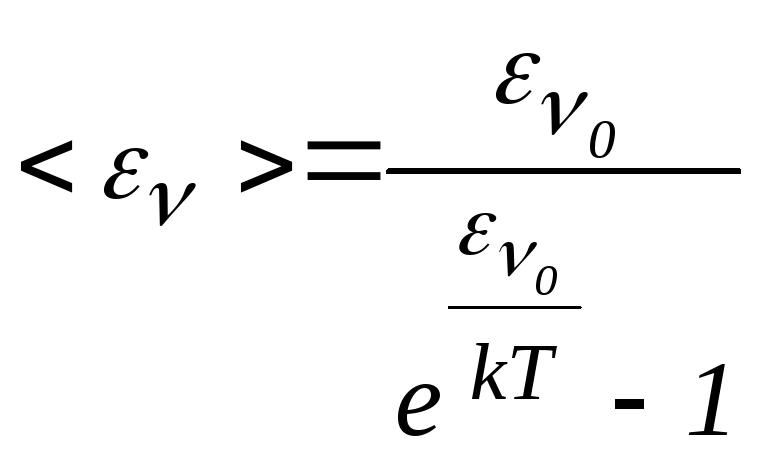Величину Планк визначив з вимоги, щоб вираззадовольняв за­гальну термодинамічну формулу Віна

.

Ця вимога зводиться до виконання співвідношення

.

Але є характеристикою лише самого осцилятора, а тому не може залежати від температуриТ- макроскопічного параметра, що визначає стан речовини і випромінювання. Величинаможе залежати лише від власної частотиосцилятора. В такому випадку, щоб ліва частина даного співвідношення була функцією лише аргументу, необхідно і достатньо, щоб, де - стала величина, яку називають сталою Планка.

Тобто, згідно з гіпотезою Планка атоми і молекули випромінюють енергію окремими порціями, або квантами, величина яких .

Отже, формула Планка для випромінювальної здатності абсолютно чорного тіла має вигляд:

, .

В області малих частот формула Планка збігається з формулою Релея-Джінса, а у випадку високих частот- з виразом, який отримав В.Він.

З формули Планка можна отримати закон Стефана-Больцмана і закон зміщення Віна.

Інтегральна випромінювальна здатність абсолютно чорного тіла

.

Введемо безрозмірну змінну інтегрування

, тоді ,;

Тоді

,

де

,

оскільки

.

Підставивши значення сталих, от­римуємо

.

Отже,

.

За відомим з досліду значенням сталої Стефана-Больцмана Планк впер­ше визначив величину сталоїh:

.

Отже, формула Планка дає змогу не тільки встановити закон Стефана-Больц­мана, але й знайти величину сталої .

Для отримання виразу закону зміщення Віна знайдемо :

.

Довжину хвилі , яка відповідає максимальному значенню, знайдемо, прирівнявши до нуля. Введемо зміннуі отримаємо

.

Розв’язання цього трансцендентного рівняння методом послідовних наближень дає .

Отже,

.

Звідси

.

Таким чином, формула Планка є повним розв’язком основної задачі теплового випромінювання, сформульованої Кірхгофом.