Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет Львовская политехника

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Вища математика / B.M

..pdf

Скачиваний:

Добавлен:

12.02.2016

Размер:

1.03 Mб

Скачать

☆

<<< < Предыдущая 12 / 92 3 4 5 6 7 8 9 > Следующая >>>

Розділ 2

ВЕКТОРНА АЛГЕБРА

2.1. Основні поняття

Вектором будемо називати напрямлений відрізок (рис. 2.1). Точка А називається початком, а точка В – кінцем.

		A1
A	a	B
A		B
		B
		A
	Рис. 2.1	Рис. 2.2

Відстань між початком і кінцем вектора називається довжиною або модулем вектора. Довжина вектора a позначається | a |.

Вектори, розташовані на одній прямій або на паралельних прямих,

називаються колінеарними.

Два вектори називаються рівними, якщо вони збігаються при паралельному переносі. (рис. 2.2).

Два вектори називаються однаково напрямленими (протилежно напрямленими), якщо вони колінеарні й у рівних їм векторів, що мають загальний початок, кінці розташовуються по одну сторону від початку (відповідно по різні сторони від початку).

2.2. Лінійні операції над векторами

Означення. Сумою вектора AB й вектора BC називається вектор AC : AC = AB + BC . Сумою вектора AB й довільного вектора PQ називається

сума вектора AB й вектора BC , рівного PQ

c = a + b

A B

(рис. 2.3)	(правило трикутника).
	D
C
c
b	B
	a
A

Рис. 2.3

Рис. 2.4

- 13 -

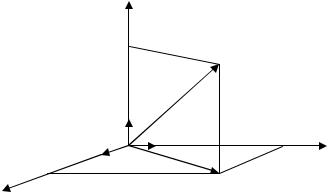
Додавання двох неколінеарних векторів a і b можна виконувати за правилом паралелограма: вектори a й b відкладаються від однієї точки А (рис. 2.4) і будується паралелограм зі сторонами AB й AC .Тоді AD = a + b .

Вектором, протилежним вектору AB , називається вектор BA : BA = - AB . За означенням вектор, протилежний нульовому вектору, є нульовий вектор.

Очевидно, a + (- a ) = 0 .
Різницею векторів a й b			(позначається a - b ) називається сума вектора
a й вектора	- b , протилежного b : a - b = a +( - b				).
Кутом між ненульовими векторами AB й AC					називається кут ВАС.
Кутом між будь-якими двома векторами				a й b називається кут між
рівними їм	векторами	із	загальним	початком.	Кут між	однаково
напрямленими векторами вважається рівним нулю.						й b , 00≤φ≤
Таким чином, якщо φ –		градусна міра кута між векторами a
1800. Означеня. Добутком ненульового вектора a					на дійсне число λ ≠ 0

називається вектор, довжина якого дорівнює добутку довжини вектора a на модуль числа λ, а напрям збігається з напрямом вектора a при λ > 0 і

протилежно напряму a при λ < 0.

Добуток вектора a на число λ позначається λa . За означенням

| λ a | =| λ |.| a |.

2.3. Координати вектора

Вектор, довжина якого прийнята за одиницю виміру довжини, називають

одиничним.

i r

Рис. 2.5

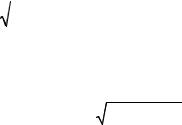
Одиничні вектори i , j , k , де

i j k й

(

= 1),

що мають

напрями додатних координатних півосей, називаються координатними

векторами або ортами.

Теорема 1 (про розкладання вектора по осях координат).

Кожен вектор a		можна представити у вигляді:
r		r	r	r
a	= ax i		+ ay j	+ zk	(2.3.1)

і притім єдиним чином.

- 14 -

Якщо вектор a представлений у вигляді (2.3. 1), то говорять, що вектор

розкладений

по

векторах i ,

j , k . Коефіцієнти ax,

ay, az –

розкладання

вектора a по одиничних векторах i

, j

і k

називають координатами вектора

даній системі координат

Оху

записують

a (ax; ay;

az ). Тоді

= ax2 + ay2 + az2 .

Нехай дана точка М(х; y; z). (рис.2.5)

Тоді

r = OM = xi + y j + zk, − це радіус-вектор точки М

(2.3.2)

де х, у, z – координати точки М, тобто

= r(x, y, z),

+ y2 + z2 , i = (1, 0, 0), j = (0,1, 0), k = (0, 0,1) .

Формула (2.3.2) представляє собою розкладання вектора OM по векторах

, j

, k .

Числа

x, y, z , що є проекціями вектора OM , називаються

координатами вектора r : x = прох r,

y = проy r,

z = проz r,

Теорема

Кожна координата суми

векторів a = a1 i + a 2 j + a3 k і

b = b1 i + b2

j + b3 k дорівнює сумі відповідних координат цих векторів; кожна

координата добутку вектора a

на число λ дорівнює добутку відповідної

координати цього вектора на число λ.

c =λa +µb ↔c = (λa1 + μb1 )i + (λa2 + μb2 ) j + (λa3 + μb3 )k

Теорема 3. У колінеарних векторів відповідні координати пропорційні.

a ׀׀b ↔b =λ a ↔	b1	=	b2	=	b3	= λ .

	a1		a2 a3

Якщо λ>0, a ↑↑b – вектори однаково напрямлені; якщо λ<0, a ↑↓b –

вектори протилежно напрямлені.

З означення колінеарних векторів випливає, що два вектори колінеарні в тім і тільки тім випадку, якщо один з них може бути отриманий множенням іншого на деяке число λ, тобто

(2.3. 3)

= λb .

Нехай вектори

, z1 ) ,

b задані своїми координатами, тобто a = ( x1 , y1

b = ( x2 , y2 , z2 ) ,

тоді векторна рівність (2.3. 3) еквівалентна трьом числовим:

x1 = λ x2 , y1 = λ y2 , z1 = λ z2 ,

з яких випливає

(2.3. 4)

2.4. Ділення відрізка в даному відношенні

Якщо M1(x1, y1, z1)

M2(x2, y2, z2)–

кінці відрізка M1M2,

а точка M(x,y,z)

ділить цей відрізок у відношенні

M1M

= λ , то координати цієї точки

MM 2

x =

x1 + λ x2

, y =

y1 + λ y2

, z =

z1 + λ z2

(λ≠-1).

(2.4.1)

1+ λ

- 15 -

Зокрема, якщо M(x, y,z) –																						середина							відрізка M1M2,							то λ=1 й
x =		x1 + x2				, y =			y1 + y2					, z =						z1 + z2				.
x =						, y =								, z =										.
	2									2					2
Приклад 1. Задано точки А(2;-3;1) і В(12;7;11). Знайти точку M(x,y,z) ,
що ділить відрізок ВА у відношенні																									BM		=				1	.
що ділить відрізок ВА у відношенні																											=					.
																									MA				3
Розв’ язання.										Вважаючи														точку				В					початковою			точкою відрізка,
знаходимо:
	12 +			1	× 2										7 -				3				11+					1		×1
	12 +				× 2			19							7 -							9	11+							×1				17
x =		3					=	19			, y =					3					=	9	, z =			3							=	17	.
x =							=				, y =										=	2	, z =										=		.
			4				2										4					2				4							2
	3														3											3
										19			9		17
Відповідь:							M					;		;				.
Відповідь:							M					;		;				.
										2			2			2
Приклад							2. Задано точки A(x1; y1;																							z1) і B(x2; y2;						z2). За допомогою

векторів виразити координати точки М, що ділить відрізок АВ навпіл. (рис. 2.6).

Розв’ язання.

Радіуси-вектори точок

А і В:

OA = (x1; y1; z1 ) ,

OB = (x2 ; y2 ; z2 ) .

За правилом додавання векторів OC = OA + OB Û OC = (x1 + x2 ; y1 + y2 ; z1 + z2 ) .

uuuur

uuur

uuuur

x + x

y + y

+ z

x + x

y + y

z + z

Тому щоOM

Û OM

;

, тобто M

;

M B

O Y

Рис.2.6.

2.5. Напрямні косинуси. Орт вектора

Модуль вектора, заданого своїми координатами (x,y,z), обчислюється за

формулою:	r	= x2 + y2 + z2 ;	напрямні косинуси (тобто косинуси кутів, які
	a

вектор a становить із додатними напрямами відповідних осей координат):

	x		y		z
cosα =	r	, cos β =	r	, cos γ =	r	,	причому cos2 α + cos2 β + cos2 γ = 1 .
	a		a		a
							r	r
								r
								a
Орт вектора визначається як							a0 =	r	.	Очевидно, що напрямні косинуси
								a
r										r0	.
вектора a є координатами орта цього вектора a											.

Приклад. Нехай A(1; 2; 0), B(3; 1; -2). Знайти напрямні косинуси вектора AB .

- 16 -

Розв’ язання. Координати

вектора

AB визначаються так:

x=3-1=2;

y=1-2=-1; z=-2-0=-2,

uuur

Тобто вектор AB = (2; −1; −2) , його довжина

напрямні

22 + (-1)2 + (-2)2

= 3;

косинуси: cosα =

, cos β = -

, cos γ = -

2.6. Скалярний добуток векторів

Скалярним добутком двох векторів називається число рівне добутку

довжин цих векторів на косинус кута між ними.

r r

cosϕ , де 0

≤ ϕ ≤ π .

(a b)

= ab

Проекція вектора

b на на

вісь, визначену вектором

a ,

дорівнює

cosϕ . Звідси випливає,

r r

ï ð arb

що скалярний

добуток (ab) =

прar b або

r r

(ab)

прr a .

Властивості скалярного добутку:

1.Скалярний добуток ненульових векторів дорівнює нулю тоді й тільки тоді, коли множники перпендикулярні.

2.Скалярний добуток двох ненульових векторів додатний, якщо вектори становлять гострий кут, від’ ємний, якщо вектори становлять тупий кут.

3.Скалярний добуток не змінюється від перестановки

співмножників.

4.	r r	r	2	→	r	=	r r

	(aa) =	a	.		a		(aa) .

5.Скалярний множник можна виносити за знак скалярного добутку: (α a, b) = α (a,b).

6.Дистрибутивність додавання векторів стосовно скалярного множення на вектор:

((a + b), c) = (a, c) + (b, c)

Вираз скалярного добутку в декартових прямокутних координатах через компоненти співмножників.

Нехай a = x1 i + y1 j + z1 k, b = x2 i + y2 j + z2 k , тоді a ×b = x1 x2 + y1 y2 + z1 z2 .

Косинус кута між векторами через їхні компоненти знаходиться за формулою:

		r r			x1 x2 + y1 y2 + z1 z2
cosϕ =	(a, b)			=		.
		r	r

		a	b		x12 + y12 + z12 x22 + y22 + z22
Умова перпендикулярності векторів: (a, b) = 0 або x1 x2 + y1 y2 + z1 z2 = 0 .
Приклад 1.					Задано три точки на площині
А(1;2), В(2;2), C(1,5;2,5). Знайти кут між векторами АВ і АС.
Розв’ зання.					Знаходимо

- 17 -

uuur	= (2			uuur	=
АВ	= (2	-1; 2 - 2) = (1; 0), АС			=
Тоді:			uuur uuur
Тоді:			АВ× АС
сosϕ =

		12 + 02 × 0, 52 + 0, 52
		12 + 02 × 0, 52 + 0, 52

(1, 5 -1; 2, 5 - 2) = (0, 5; 0, 5),

=	0, 5	=	1	, ϕ = π .

0, 5		2		4

Приклад 2. Обчислити скалярний добуток.

(2m + 3n) ×(4m - 6n), де m й n − одиничні взаємно перпендикулярні вектори. Розв’ зання.

Знаходимо, використовуючи властивості скалярного добутку.

ur r	ur r
(2m + 3n) ×(4m - 6n) =
urur	rur	urr	r r	= 8 ×1+12 ×0	-12 ×0 -18 ×1 = -10,
2 × 4 (mm) + 3	× 4 (nm) - 2	×6(mn) - 3×6(nn)		= 8 ×1+12 ×0	-12 ×0 -18 ×1 = -10,
де (m, m) = (n, n) = 1, (m, n) = (n, m) = 0 .
Приклад 3.		При	якому	значенні	α вектори a = (2; - 3; 4), b = (α; - 6;8)

паралельні?

Розв’ язання. Вектори паралельні, якщо їхні координати пропорційні, тобто:

α = −6 = 8 . Звідси знаходимо: α=4.

2 -3 4

Приклад 4.

							2π
Дано:	r		r		r	r		. Знайти, при якому значенні α вектори
	a	= 2,	b	=	5, (a, b) =
	a	= 2,	b	=	5, (a, b) =		3
p = α a +17b і							3	перпендикулярні.
p = α a +17b і					q = 3a - b			перпендикулярні.
Розв’ язання.

Умова перпендикулярності векторів: pq = 0 . Звідси

urr

r r

pq =

(α a +17b)(3a - b) =

3α (a, a)

r r

= 3α

+ 51

(a, b) -17(b ×b)

3α × 4 + (51-α ) ×10 ×

-17 × 25

Приклад

Вектори

a - b

r r

+17 ×3(b, a) -

cos

2π

-α

cos

2π

-17

= 0 α = 40.

a й b утворюють кут

1200,

= 3,

= 5 .

Знайти

Розв’ язання.

r r

r r r r

r r

a - b

(a - b)(a - b) =

- 2(a, b) +

- 2

cos1200 +

9 - 2 ×3×5 ×

+ 25 = 9 +15 + 25 = 49 = 7 .

Приклад 6. При якому значенні α вектори a = (1; α ; - 2) й b = (α ; 3; - 4) перпендикулярні?

Розв’ язання.

Обчислимо скалярний добуток векторів і прирівняємо його до нуля.

a ×b = 1×α +α ×3 + (-2) ×(-4) = 4α + 8 = 0 ,

звідси знаходимо α=-2.

- 18 -

Приклад	7. Задано три вектори a, b, c . Довести, що вектор
d = (b, c)a - (a, c)b	перпендикулярний вектору c .

Розв’ язання.

Умова перпендикулярності векторів − рівність нулю їхнього скалярного добутку. Помножимо скалярно вектор d на c й, у силу властивостей скалярного добутку, одержимо:

d ×c = ((b, c)a - (a, c)b)c = (b, c)(a, c) - (a, c)(b, c) = 0 .
Приклад 8. Знайти вектор a , колінеарний вектору	b = (2; -1;0) , якщо
a ×b = 10 .
Розв’ язання.
Вектор a = λb = λ(2; -1; 0) ( оскільки колінеарні), тоді	їхній скалярний
добуток a ×b = λ(2 × 2 -1×(-1) + 0 ×0) = 5λ = 10 .

Звідси знаходимо: λ=2, a =2(2; -1; 0) =(4; -2; 0).

Приклад 9	. Вектор b \|\| a , де a =(8; -10; 13) і утворює з віссю OZ гострий
		r
кут. Знаючи, що		b	= 37 , знайти його координати.

Розв’ язання.

З умови колінеарності вектор b = λ a, b = (8λ; -10λ;13λ), при цьому повинна

виконуватися умова 13λ>0,

тобто, λ>0

(вектор

b утворює з віссю OZ

гострий кут). Модуль вектора b дорівнює

uur

= λ 2 (82 + (-10)2 +132 ) =

64 +100 +169

333

9 ×37

звідси:

. Беремо λ =

, λ = ±

(за умовою λ>0). Виходить, b =

; -

;

Приклад 10.

Задано три вектори

a = (3; -1), b = (1; -2), c = (-1;7).

Знайти

розкладання вектора p = a + b + c по векторах

a й b .

Розв’язання. За правилом додавання

векторів

маємо:

p =

(3+1-1; -1-

2+7)=(3; 4)

Розкласти вектор p

по векторах a й b

означає: знайти α і β такі,

що буде

виконуватися рівність p = α a + β b .

Два вектори рівні, якщо рівні їхні відповідні компоненти:

3α +

β = 3

α = 2;

β = -3 .

2β =

-α -

p = 2α - 3b .

Отже,

r r

Приклад 11. Задано:

= 4,

= 3,

= 2, a ^ b, a ^ c,

(b, c) = 120

Знайти (2a + 3b - c)(a - 2b + 3c)

Розв’язання.

Використовуючи означення й властивості скалярного добутку, одержимо:

- 19 -

(2a

r r

+ 3b - c)(a - 2b + 3c) =

r r rr

r r

- 3

+ 3ba - ca

- 4ab - 6

+ 2cb + 6ac

+ 9bc

- 6

- 3

- ab + 5ac

+11bc

× 42 - 4 ×3×cos 900 + 5 × 4 ×2 ×cos 900 +11×3×2 ×cos1200 - 6 ×32 - 3×22 = -67

	ur		r		ur r	0
Приклад 12. Задано:	m	= 4,	n	= 3,			.
					(m, n) = 60

Знайти величину кута між векторами m - n

й m + n .

Розв’ зання.

Використовуючи скалярний добуток, знаходимо

r ur

cosϕ =

- n)(m + n)

m - n

+ n

Обчислюємо

= 42

- 32

= 7 ;

(m - n)(m + n) =

rur

m - n

- n)(m

- n ) =

- 2nm

16 - 2 ×3

× 4 ×cos 600 + 9 =

13;

rur

m + n

+ n)(m

+ n ) =

+ 2nm +

16 + 2 ×3

× 4 ×cos 600 + 9 =

37;

cosϕ =

, звідки ϕ = arccos

13 ×

481

2.7. Векторний добуток

Векторним

добутком

векторів

називається

вектор

що

c ,

задовольняє умовам:

перпендикулярний обом векторам-співмножникам a й b ,

до

2) якщо дивитися з його кінця, то найкоротший поворот на кут φ від a

тобто трійка векторів

b відбувається проти годинникової стрілки,

b ,

c є правою.

модуль векторного добутку дорівнює

sin ϕ .

r r

Векторний добуток позначається c = a ´b або c

= a, b .

Модуль векторного добутку чисельно дорівнює площі паралелограма, побудованого на

векторах a

й b

sin ϕ .

S =

a ´b

або

Площа трикутника, побудованого на векторах a й b

Основні властивості векторного добутку:

1.2.	r	r	r	r	r	r	r	r	r	r
1.2.	a	´b	= -b	´ a;	α (a	´b ) = (α a )´b			= a	´(αb );

1 × r ´ r

: S∆= 2 a b

3. r ´( r + r) = r ´ r + r ´ a b c a b a

r c.

Векторний добуток через координати векторів-співмножників виражається як

- 20 -

			r	r	r
r	r		i	j	k
r	r	=	x1	y1	z1	.
a	´b	=	x1	y1	z1	.
			x2	y2	z2

Необхідною й достатньою умовою колінеарності векторів є рівність нулю їхнього векторного добутку.

Приклад 1. Обчислити векторний добуток векторів a = 2m + 3n й b = 5m - n . Розв’ язання. Використовуючи властивості векторного добутку, одержимо:

r r

r ur

a, b

+ 3n, 5m

- n

= 2m, 5m

+ 3n, 5m

- 2m, n

- 3n, n .

Оскільки			2mur, 5mur			= 0,	3nr	,

ar	, br	= 15	nr	, mur	+ 2 nr, mur		= 17

n	= 0,	mur, nr	= - nr	, mur	, одержимо

nr, mur .

Приклад 2. Задані 3 вершини паралелограма A(1;-1;2); B(5;-6;2); C(1;3;-1). Знайти його площу.

Розв’ язання.

uuur uuur

AB =

(4; -5;0),

AC = (0; 4; -3).

Площа

AB ´ AC

uuur

-5 0

AB ´ AC

= 15i

+12 j -

16k ;

-3

= 25(кв. од.) .

S =

152 +122 + (-16)2

625

Приклад 3. Знайти площу трикутника, побудованого на векторах

a = m + n й

b = 2m - n ,

urr

якщо

= 1, mn = .

Розв’язання.

r r

S∆=

a, b

, a, b

+ n, 2m - n

= m, 2m

+ n, 2m

- m, n

- n, n

. Оскільки

ur r

r ur

= 0,

m, 2m

n, n

m, n = - n, m , то a, b = 2 n, m +

n, m =

3 n, m

×sin π =

S∆=

n, m

3 ×

×1× 2 ×

(кв. од.).

2.8. Мішаний добуток векторів

Мішаним добутком векторів a, b, c називається число, отримане в результаті

скалярного множення одного з даних векторів на векторний добуток двох інших:

r r

(a, b, c )

= (a ´b )×c = a ×(b ´ c ).

- 21 -

Властивості:

r r

r r r

(a, b, c )

= (b, c, a ) = (c, a, b ) = − (b, a, c ) = − (c, b, a ) = − (a, c, b ).

+ α

r r

властивість лінійності.

(α1a1

2 a2 , b, c ) = α1 (a1

, b, c) + α2

(a2

, b, c) –

3.Модуль мішаного добутку дорівнює об'єму паралелепіпеда,

побудованого на векторах a, b

Об'єм трикутної піраміди дорівнює V = 1

r	, тобто V =	r r r	.

і c		(a, b, c )
r	r r

(a, b, c ) .

4.Якщо вектори задані своїми координатами в ортогональній системі координат:

r	= ( x1	; y1 ; z1 );	r	r	= ( x3 ; y3 ; z3 ) ,
a			b = ( x2 ; y2 ; z2 ); c			то мішаний добуток можна
знайти за формулою:
	r	x1	y1	z1
		r r	y2	z2 .
	(a, b, c ) = x2

x3 y3 z3

З означення мішаного добутку випливає, що необхідною й достатньою умовою компланарності векторів є рівність нулю їхнього мішаного добутку:

r r r		x1	y1	z1	= 0 .
r r r	або	x2	y2	z2
(a, b, c ) = 0	або	x2	y2	z2
		x3	y3	z3

Приклад 1. Обчислити мішаний добуток векторів: a = (2; − 1; 3), b = (1; 4; − 2), c = (−3; 2; 5) .

r	r	r	2	−1	3

			1	4	−2	=40+6-6+36+8+5=89.
Розв’язання. (a, b, c ) =
			−3	2	5

Приклад 2. Задано вершини піраміди A(2;3;1), B(4;1;-2), C(6;3;7), D(-5;-4;2).

Знайти її об'єм і довжину висоти, опущеної з вершини D.

Розв’язання.

Об'єм піраміди дорівнює

V =

(

)

; або V =

Sосн.H H =

осн.

Знаходимо

= (2; −2; −3),

= (4;0; 6),

= (−7; −7;1),

Sосн.

(

−2

−3

−2

−3

= 260. Тоді V =

) =

260 (куб.од.).

−7

−14

−7

- 22 -

<<< < Предыдущая 12 / 92 3 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в папке Вища математика

#
12.02.20161.03 Mб58B.M..pdf
#
12.02.20161.29 Mб53В.М.-iнтеграли.pdf