Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет Львовская политехника

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Вища математика / В.М.-iнтеграли

.pdf

Скачиваний:

Добавлен:

12.02.2016

Размер:

1.29 Mб

Скачать

☆

1 / 121 2 3 4 5 6 7 8 9 10 11 12 > Следующая >>>

Розділ 7

ВИЗНАЧЕНИЙ ІНТЕГРАЛ

7.1.Означення, властивості, геометричний зміст

визначеного інтеграла

До поняття визначеного інтеграла приводять задачі обчислення площ, об'ємів тіл, довжини дуги кривої, фізичні задачі.

Нехай на відрізку [a,b] визначена функція y=f(x). Розіб'ємо відрізок на

n частин точками a = x0 < x1 < L < xi−1 < xi	< L < xn	= b .
На кожному з відрізків [ xi−1 , xi ]	візьмемо довільну точку ξi		й складемо
n
суму Sn = ∑ f (ξi )Dxi , що називається інтегральною сумою.
i=1
Якщо існує скінченна границя		інтегральної суми	Sn при

λ = max {Dx } ® 0 , що не залежить від способу розбивки області на елементарні

1≤i≤n i

ділянки й вибору точок , то вона називається визначеним інтегралом функції f(x) на відрізку [a, b] й позначається

∫ f (x)dx = lim ∑ f (ξ i ) xi .

λ →0 i=1

Функція f(x) у цьому випадку називається інтегровною

на відрізку

[a, b] .

y=f(x)

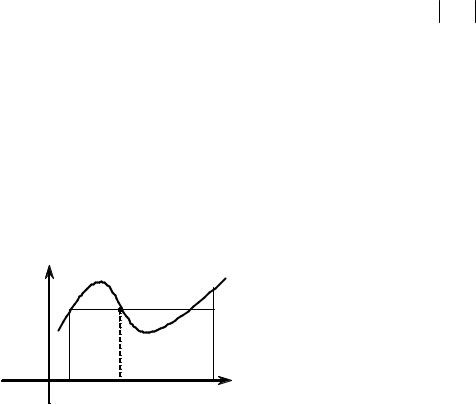
Геометричний зміст

визначеного

інтеграла:

якщо f ( x) ³ 0

x [a, b] ,

то

∫ f ( x) dx

чисельно

дорівнює

площі

криволінійної

трапеції

Рис. 7.1

основою

[a,b],

обмеженої

прямими

x=a, x=b

кривою y=f(x) (рис. 7.1).

Властивості визначеного інтеграла.

1. ∫ f ( x) dx = −∫ f ( x) dx .

∫ f (x)dx = 0 .

Лінійність інтеграла. Якщо f ( x)

g ( x) – функції,

інтегровні на

[a, b] , то

(x) ± g

а) ∫ cf ( x) dx = c∫ f

( x) dx, (c = const ) ; б) ∫ ( f

(x))dx = ∫ f (x)dx ± ∫ g(x)dx.

- 90 -

Поєднуючи властивості а) і б), можна записати властивість лінійності

		b	b	b
визначеного інтеграла: ∫(c1 f ( x) + c2 g ( x))dx = c1			∫ f ( x) dx + c2 ∫ g ( x) dx.
		a	a	a
4.	Адитивность інтеграла. Якщо f ( x)		–	функція інтегровна на [a, c] й
[c, b] , де c Î(a, b) , то вона інтегровна на [a,b] й
b	c	b

∫ f ( x )dx = ∫ f ( x )dx + ∫ f ( x )dx.

a	a	c
		b
5.	Якщо a < b й	f ( x) ³ 0 , те∫ f ( x) dx ³ 0 , причому рівність нулю можлива
		a
тільки в тому випадку, коли f ( x) º 0 , x (a,b) .
		b	b
6.	Якщо a < b	й f ( x) ³ g ( x) , то ∫ f ( x) dx ³ ∫ g ( x) dx – теорема про
		a	a

інтегрування нерівностей.

7. Якщо f ( x) – функція, інтегровна на [a,b], то f ( x) – інтегровна на [a,b] і справедлива нерівність:

	b	b
	∫ f (x)dx	≤ ∫	f	(x)	dx – теорема про модуль визначеного інтеграла.

	a	a
8.		Теорема про оцінку визначеного інтеграла. Якщо m £ f ( x) £ M , m–
найменше, М –				найбільше значення функції f(x) на відрізку [a; b],то
				в
	m(в − а) ≤ ∫ f (x)dx ≤ М (в − а).
				а
9.		Теорема про середнє значення. Якщо f ( x) неперервна "x Î[a, b] , то

a ξ

Рис. 7.2

висотою, рівною f (ξ )

b x

(рис. 7.2).

$ξ Î(a, b) , що ∫ f (x)dx = f (ξ )(b − a).

	a
Геометричний зміст				теореми:
нехай f ( x) ³ 0		x [a, b] ,		тоді	існує
принаймні	одна	точка	ξ Î(a, b) , що
площа	криволінійної			трапеції,
обмеженої	зверху		неперервною
кривою y = f ( x )		буде	рівна		площі

прямокутника з тією ж основою й Значення f (ξ ) називається середнім

значенням функції на відрізку [a, b].

10. Якщо функції f (x) й ϕ ( x) – неперервні на [a, b], а ϕ ( x) зберігає знак на цьому відрізку, то (узагальнена теорема про середнє):

b	b
∫ f ( x)j( x) dx = f (ξ ) ∫ j( x) dx, a < ξ < b
a	a

- 91 -

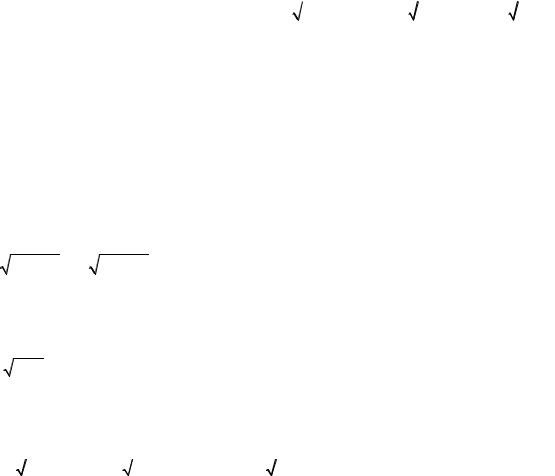
11.	Якщо неперервна функція f (x), x [− l,l] – парна, то
l	l
∫ f	(x)dx = 2∫ f (x)dx .
−l	0
	l
	Якщо f (x) – непарна, то ∫ f (x)dx = 0 .
	−l
	7.2. Методи обчислення визначеного інтеграла

Фундаментальним результатом математичного аналізу й поворотним моментом у розвитку інтегрального числення з'явилося відкриття зв'язку між визначеним і невизначеним інтегралами. Це дозволило визначені інтеграли обчислювати не як границі інтегральних сум, а через невизначені інтеграли.

Теорема. Похідна визначеного інтеграла від неперервної функції по його верхній межі існує й дорівнює значенню підінтегральної функції у верхній межі, тобто

′

∫ f (t)dt = f (x) .

′

= e− x

′

= −

sin3 x .

Наприклад, а) ∫ e−t

; б) ∫

sin3 tdt

−∫

sin3 tdt

Формула

Ньютона-Лейбніца:

b∫ f (x)dx = F (x)

ba = F (b) − F (a)

–

основна

формула інтегрального числення, що встановлює зв'язок між визначеним і невизначеним інтегралами й дозволяє знаходити значення визначеного інтеграла як різницю значень первісної на верхній і нижній межах визначеного інтеграла.

Приклади.

Обчислити визначені інтеграли:

		e				dx									e			d (ln x)
		∫											=		∫												= arcsin ln x							1e = arcsin ln e − arcsin ln1 =



						− ln			2									1− ln					2
1. 1 x 1						− ln					x				1			1− ln							x
		arcsin1− arcsin 0 = π − 0 = π .
		−π											−π					2										2				−π														−π
		−π				3							−π				(1− sin					2										−π					− 1									−π			5
		4		cos		3		xdx						4								2		x)d (sin x)									4				− 1									4			5
2.												=																			=		(sin x)							d (sin x) −								sin			xd (sin x) =
																																							3											3
																																							3											3
		∫			3 sin x								∫																1			∫														∫
		∫			3 sin x								∫							(sin x)3												∫														∫
		−π											−π							(sin x)3												−π														−π
		2												2					−π														2													2
	3						2			3				8										3				2			π					2		π						3			8		π			8	π
							2							8														2								2											8					8

		(sin x)3 −										sin 3 x							−	π4	=					sin 3 (−						)	− sin			3 (−					)		−		sin 3			(−				) − sin 3 (−		)	=
	2	(sin x)3 −								8		sin 3 x								π4	=			2		sin 3 (−					4	)	− sin			3 (−					)		−	8	sin 3			(−	4			) − sin 3 (−		)	=
	2									8										2				2							4								2					8					4				2
										2																8															2
			3															3

							2			3		−1				−							2				3		−1	= −		9	+		21			2				3
																																									.
																																									.
		2				2																2										8 16					2
		2				2												8				2										8 16					2

- 92 -

					π										π										π			dx								π										×tgx)
					4			1							4					dx					4						1					4				d (				2
					4			1							4					dx					4			cos2 x			1					4				d (				2
3. I = ∫0										dx =					∫0									= ∫0						=						∫9												=
							1+ sin2 x										2sin2 x + cos2 x										2tg 2 x +1												(			×tgx)2 +1
							1+ sin2 x										2sin2 x + cos2 x										2tg 2 x +1				2								(		2	×tgx)2 +1
1													π		1										π						1
													π
												4																																			2
			arctg(						2 ×tgx)			4		=					arctg(			2 ×tg				- arctg0 =											arctg								2 =			arctg	2 .

																									4																						2
	2											0						2							4						2																2
												0
				−1												−1																																		π		π		π

			3												3
			3					dx							3					d (x +1)									x +1			3 −1													3			1
4.			∫					dx							∫					d (x +1)									x +1			3 −1													3			1							.
													=												= arcsin										= arcsin												- arcsin		=		-		=

											2										2		2
	0						3 - 2x - x								0					-(x +1)		+ 2				2					0														2			2 3 6 6
		π																		π														π
	2																		2												2
	2																		2												2
5.		∫				cos x − cos3 xdx = ∫ cos x(1 − cos2 x)dx = ∫																																sin x					(cos x)1 2 dx =
5.		∫				cos x − cos3 xdx = ∫ cos x(1 − cos2 x)dx = ∫																																sin x					(cos x)1 2 dx =
	− π																			− π													− π
	2																		2																2

Скористаємося парністю підінтегральної функції.

π			π							π
π			π					3		2
2			2
2			2		(cos x)1 2 d (cos x) = -2 ×			(cos x)2
= 2∫ sin x (cos x)1 2 dx = - 2∫					(cos x)1 2 d (cos x) = -2 ×			(cos x)2
0			0						3
0			0					2		0
6. Обчислити середнє значення функції


f (x) = cos	π	×	1		на відрізку 0;	1	.
f (x) = cos		×	(1- x)	2	на відрізку 0;		.
1	- x		(1- x)			2

=4 .

Розв’ язання. Середнє значення функції за теоремою про середнє дорівнює:

	1	b		1			1
f (ξ ) =		∫ f (x)dx, ãäå	b - a =		-0	=		.

	b - a a		2			2

∫ cos

dx = ∫ cos

= sin

- x)

1- x

- x

1- x (1

1- x

= sin 2π - sin π = 0 .

Отже,	середнє значення функції дорівнює
f (ξ ) =	1	×0 = 0 .
f (ξ ) =	1	×0 = 0 .
	1

	2	π
		π
		2	sin x
7. Оцінити інтеграл ∫			sin x	dx .
7. Оцінити інтеграл ∫				dx .
		π	x
		4

Точне значення інтеграла в цьому випадку знайти не можна, тому що первісна не виражається через елементарні функції.

Для дослідження поведінки підінтегральної функції f (x) = sin x на відрізку x

π	π	знаходимо її похідну:
;		знаходимо її похідну:
4	2

- 93 -

не повинні

ϕ (t )

′	x cos x − sin x			π

			=	x < tgx, x
		2
f (x) =	x				4

π	=	(x − tgx)cos x		< 0
π		(x − tgx)cos x
;		x	2
3		x

Підінтегральна функція f (x) =	sin x	спадаає на відрізку	π	;	π	, тому що її
	x
			4		2

похідна

f ′( x) < 0. .

Найменше

значення

функції

m = f

, а найбільше

значення

функції

2 2

sin x

2 2

M = f

. x

;

має місце нерівність:

≤

sin x

Скориставшись теоремою про оцінку інтеграла, одержимо:

≤

∫

dx ≤

sin x

8. Оцінити абсолютну величину інтеграла ∫

dx .

1+ x8

Оскільки

sin x

≤ 1,

то

при

x > 10

виконується

нерівність

sin x

≤ 10 −8 .

1 + x 8

Використовуючи властивість 7, одержимо

sin x

dx < (19 − 10)10−8 < 10

−7 .

∫

< ∫

101 + x 8

1 + x 8

Заміна змінної в визначеному інтегралі

Нехай функція

f ( x) неперервна на [a, b] , а функція х=ϕ (t )

–

монотонна

й має неперервну похідну на відрізку [α , β ] , де ϕ (α ) = a ,

ϕ (β ) = b ,

тоді має

місце

формула

заміни

змінної

визначеному

інтегралі

′

∫ f (x)dx = ∫

f (ϕ (t))ϕ (t )dt .

Зауваження.

Заміну

змінної

інтегрування

звичайно

роблять

за

допомогою монотонних неперервних функцій, тому що монотонність гарантує однозначність як прямої, так і оберненої функції. При цьому, якщо змінна t змінюється в проміжку [α;β], значення функції

виходити за межі проміжку [a, b].

Відзначимо, що до інтегралів виду ∫		dx	застосовна

	(x − α )n	ax2 + bx + c
	(x − α )n	ax2 + bx + c

підстановка x-α=1/t (підстановка приводить до менш громіздких викладень, ніж тригонометричні підстановки).

2		dx
Приклад 1. Обчислити інтеграл. ∫		dx			.


			2
1	x x			−1
1-й спосіб: застосуємо підстановку x=1/t. Знайдемо межі:
інтегрування для змінної t . Маємо t=1/x,			тоді при x=1 змінна t приймає

- 94 -

значення, рівне 1 (нижня межа інтегрування). При x=2 змінна t дорівнює 1/2 (верхня межа інтегрування). Таким чином, при зміні змінної х від 1 до 2 змінна t, монотонно спадаючи, змінюється від 1 до ½. Функція x=1/ t – монотонна й неперервно диференцційовна функція на відрізку [1/2;1]. Отже,

					x =	1	, dx = -				dt		,		1
2					x =	t	, dx = -					t 2	,		1				t
2		dx				t						t 2		2		tdt			t		dt			1
∫		dx			x = 1		t = 1,							= -∫		tdt		= ∫			dt		= arcsin t	=


	x x		2	-1												1 -1				1- t		2
1	x x			-1						1					1 t 2	1 -1		1		1- t				2
																								1
					x = 2 t =							.
																	t 2	2


										2
= arcsin1-					arcsin			1	= π - π					= π .
= arcsin1-					arcsin				= π - π					= π .
							2		2			6		3

2-й спосіб:

														1
2		dx			2			dx			2			d		1
2					2						2			d
∫					= ∫							= -∫		x
																	= - arcsin
																		x
	x x		2	-1			2	1-	1					1	2
1	x x			-1	1	x	2		1		1			1
													1-
									x	2
										2
														x

= - arcsin	1	+ arcsin1 = - π + π = π .

2		6	2	3

3-й спосіб:

x =

, dx = -

cos tdt

;

sin t

sin2 t

cos t

-1 =

; x = 1

×cos tdt

sin t

∫

= -∫ sin t ×

= ∫ dt = t

= .

sin

t ×cos t

1 x

-1

sin t = 1 t =

; x

sin t =

t = π .

Приклад 2. Обчислити інтеграл

I = ∫ a 2 − x 2 dx .

x = a sin t .

x = 0 ,

Заміна:

Визначимо межі інтегрування для змінної t. Нехай

тобто

беремо

рівним нижній

межі

інтегрування

вихідному

інтегралі. Тоді

в якості

можна взяти будь-який

розв’язок

рівняння

a sin t = 0 , наприклад t = 0 . При знаходженні верхньої межі для змінної t

замість х підставляємо верхню межу інтегрування, рівну а,		і розв’зуємо
рівняння a = a sin t , звідки sin t = 1,	t = π + 2πn, n z , тобто рівняння має
	2	t = π , (при
нескінченну множину розв’язків. При цьому, взявши розв’язок
		2
n = 0 ), ми одержимо, що при зміні t	від 0 до π змінна х буде монотонно
	2

змінюватися від 0 до а. Таким чином,

- 95 -

x = a sin t ,

dx = a cos tdt

I =

a 2 − a 2 sin2 ta cos tdt = a 2

cos 2 tdt =

∫

x = a,

t = π

2 1

+ cos 2t

a 2

sin 2t

a 2 π

sinπ

πa

= a

∫

dt =

t +

2 =

− ln 2

Приклад 3. Обчислити інтеграл I =

∫

1 − e2 x dx .

Функція

1 − e2 x

― неперервна й монотонна на проміжку [-ln2;0]. Вважаючи

t = 1 − e2x , знаходимо межі інтегрування для змінної t. При x=0

одержимо:

t=0; при x=-ln2 знаходимо: t =

1 − e−2 ln 2

1 − e−ln 4

x =

ln(1 − t 2 )

Очевидно,

обернена

функція,

рівна

–

неперервно

диференційовна на проміжку 0 < t <

, тоді

−ln 2

1 − e

2 x

= t 2 ,−2e2 x dx = 2tdt,

I =

1 − e2 x dx =

∫

dx =

− tdt

tdt

e2 x

t 2 − 1

2 (t 2

− 1)+ 1

− 1

t − 1

3 2

t 2 dt

I = ∫

∫

dt = t +

2 −

2 − 1

t +

+ 1

ln(2 −

)2 =

+ ln(2 −

2π

I =

При

обчисленні

інтеграла

∫

застосовуючи

підстановку

+ cos x

t = tg

знаходимо

нижню

межу

інтегрування

t = tg0 = 0 ,

верхня межа

t = tgπ = 0 . Тоді

I = 2∫

= 2∫

= 0 ,

(1 + t

1 − t 2

2 + 3

0 t

2 +

)

1 + t

що неможливо, тому що підінтегральна функція

> 0 .

Пояснюється

2 + cos x

це тим, що функція tg

в точці x = π [0, 2π] терпить розрив й, отже, не має

- 96 -

неперервної похідної. Підстановка t = tg

незастосовна на проміжку [0,

Наведений інтеграл може бути обчислений у такий спосіб.

2π

x − π = t

∫

0 → −π

= ∫

= 2

∫

=∫

+ cos x

− cos t

2 t

2π → π

−π

1 + 2 sin

sin2

+ 1

2 t

2 sin

π		dctg			t			4		ctg	t	π		4 π		2π
					t						t	π


= −2∫		2					=−			2			=		=
									arctg								.
									arctg								.
0	3	+	1	ctg 2		t		3		3				3 2		3
0		+		ctg 2				3		3				3 2		3
	2	2				2						0
	2	2				2						0

2π].

Відзначимо, що на відміну від заміни змінної в невизначеному інтегралі, у визначеному інтегралі не потрібно виконувати обернену

підстановку, тобто переходити у відповіді до старої змінної.

При використанні формули заміни змінної в визначеному інтегралі необхідно перевіряти виконання умов:

1) Функція x = ϕ (t) – неперервно диференційовна на відрізку [α , β ] або [β ,α ] (α ³ β або α £ β ) осі ot .

2)При зміні t від α до β значення функції x = ϕ (t) не виходять за межі відрізка [a, b].

3)ϕ (α ) = a, ϕ (β ) = b .

π			dx
Приклад 4. При обчисленні інтеграла ∫			dx

	sin	2	x + cos	2	x
0	sin		x + cos		x
0

формальне застосування формули заміни змінної інтегрування приводить до наступного результату:

cos2

∫

= ∫

sin

x + cos

+ tg

t= tgx

x = 0 t = 0 x = π t = 0

dt = dx cos2 x

= ∫ dt = 0 .

0 1 + t 2

З іншого боку,

dx = x

π0 = π

∫ sin 2

x + cos2

∫

У цьому випадку перераховані умови застосовності формули заміни

змінної порушуються, тому що функція t = tgx в точці x = π [0;π ]

терпить

розрив й, отже,

не має неперервної похідної.

Підстановка

t = tgx

незастосовна на проміжку [0;π ].

x9 − 3x7 + 4x5

− 2x3 + x + 2

Приклад 5. Обчислити інтеграл I = ∫

cos

−π

- 97 -

Розв’ язання. Представимо інтеграл у вигляді суми двох інтегралів,

тоді

x9 - 3x7

+ 4x5 - 2x3 + x

I = ∫

dx + 2

∫

cos

−

Скористаємося властивістю (11) визначених інтегралів, тоді, оскільки

функція

- 3x7 + 4x5 - 2x3 + x

непарна, як частка непарної й парної функції, а

cos 2 x

проміжок інтегрування симетричний відносно початку координат, перший

інтеграл дорівнює нулю. Тоді, в силу парності функції

cos2 x

I = 2 × 2∫

4tgx |

= 4 tg

- tg0 = 4 .

0 cos

Приклад 6. I

= ∫

sin 3 x cos5 x

Застосуємо підстановку t = tgx , тоді x = arctgt – монотонна, неперервно

диференційовна функція.

При

x = π одержимо

t = 1,

при

x = π

t =

тобто

1 £ t £

;

dx =

1 + t 2

−

I = ∫

= ∫

= ∫t 4 dt = = 4t 4 |

= 4 (

3)4 -1 = 4(8 3

-1)

1 t 4

1 (1 + t 2 )4

(1 + t 2 )4

4,5

Приклад 7. I

= ∫

1 +

-1

Скористаємося заміною: 3

= t . Визначимо новий проміжок інтегрування.

2x -1

Якщо x = 1,

то t = 1; якщо x = 4,5 ,

те t = 3

= 2 . Отже,

2x-1=t3,

2dx=3t2dt,

dx=3/2t2dt.

3 2 t 2 dt

3 2 (t 2 -1)

2 dt

I =

∫

1 + t

dt =

∫ (t -1)dt + ∫

1 + t

2 1 1 + t

2 1

(t -1)2

+ ln(1+ t)

+ ln 3 - ln 2

+ ln

Формула інтегрування частинами: ∫ u × dv = u × v

- ∫ v × du .

Приклади.

1. I = ∫ x log2 xdx .

- 98 -

Покладаємо u = log2									x, тоді du =				dx	, dv = xdx, v =					x2	.
Покладаємо u = log2									x, тоді du =					, dv = xdx, v =						.
													x ln 2				2
Отже,
I = log2 x ×			x2			-	1	2 x2	×	dx	= log		2 × 2 - log2		1×	1	-	1		2	xdx = 2 -	1	×	x2	2 =
			x2		2		1			dx						1		1		2		1		x2
												2						2 ln 2		∫
2					1	2		∫		x ln 2					2			2 ln 2		∫		2 ln 2 2			1
	1			1				1		3	.									1
2 -	1	× 2 +		1				= 2 -		3
2 -		× 2 +		4 ln 2				= 2 -
	2 ln 2			4 ln 2						4 ln 2

2. I = ∫ x × arctgxdx .

Покладаємо u = arctgx, тоді du =

dv = xdx,

v =

, тоді:

+ x2

dx 9

+1)

-1

∫0

I = arctgx ×

arctg3 -

(x - arctgx)

1+ x2

2arctg3

arctg3 -

(3 - arctg3) = 5arctg3 -

π 2

3. Обчислити інтеграл: I n = ∫

sinn xdx .

Нехай u = sinn −1 x , тоді du = (n - 1)sinn−2 x cos xdx , dv=sinx dx, v=-cosx.

I n = - cos xsinn x

π 2 + (n - 1)π∫2 sinn−2 x(1 - sin2 x)dx = (n - 1)π∫2 sinn−2 xdx -

− (n − 1)I n = (n − 1)I n−2 − (n − 1)I n .

Отже, I n =

n - 1

I n−2 . Отримане

рекурентне

співвідношення дозволяє для

будь-якого натурального n одержати значення інтеграла

(2k - 1)! !

π 2

I 2k = (2k - 1)(2k - 3)...3 ×1 I0 =

π , де I0 = ∫ dx = π .

2k (2k - 2)...2

(2k )! !

При n=2k+1 знаходимо

π 2

2k (2k - 2)...2

(2k )! !

I 2k +1 =

, де I

1 = ∫ sin xdx = 1.

(2k

- 1)(2k - 3)...3 ×1

(2k + 1)! !

π 2

Крім того,

∫

cosn xdx = ∫

sinn xdx (що очевидно з геометричних міркувань і

можна перевірити заміною t = π - x ).

Таким чином,

(n -1)!!π

π 2

якщо n

- парне

∫ cosn xdx = ∫

n!!

sinn xdx =

(n -1)!!

якщо n - непарне

n!!

- 99 -

1 / 121 2 3 4 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в папке Вища математика

#
12.02.20161.03 Mб58B.M..pdf
#
12.02.20161.29 Mб53В.М.-iнтеграли.pdf