Вбудована функція odesolve

Вбудована функція odesolve призначена для вирішення диференціальних рівнянь, лінійних щодо старшої похідної. На відміну від інших функцій бібліотеки Differential Equation Solving, odesolve вирішує диференціальні рівняння, записані в загальноприйнятому в математичній літературі вигляді.

• Функція odesolve вирішує для рівнянь вигляду а(x)у(n) + F(x, у, у',..., у^(n-1)) = f(x) задачу Коші у(x₀) = y₀, у'(x₀) = y_0,1, y''(x₀) = y_0,2,...,у^(n-1)(x₀) = y_0,n-1 або просту граничну задачу у(k) (a)=y_a,k, у(m) (b)=y_b,k, 0<= k<= n-1, 0<= m<= n-1.

• Функція odesolve вирішує поставлену задачу методом Рунне - Кутта з фіксованим кроком. Для вирішення завдання методом Рунне - Кутта з автоматичним вибором кроку потрібно клацнути в робочому документі на ім'я функцій правою кнопкою миші і позначити в спливаючому меню пункт Adaptive.

• Звернення до функції має вид

Y:=odesolve(x,b,step) або

Y:=odesolve(x,b),

де Y - ім'я функції, що містить значення знайденого рішення, x - змінна інтегрування, b - кінець проміжку інтегрування, step - крок, який використовується при інтегруванні рівняння методом Рунге-Кутта.

• Перед зверненням до функції odesolve необхідно записати ключове слово Given, потім ввести рівняння і початкові або граничні умови. При введенні рівняння і умов завдання використовується знак символьної рівності (<Ctrl>+<=>), а для запису похідних можна використовувати як оператора диференціювання, так і знак похідної, наприклад, другу похідну можна вводити у вигляді або у виглядіy''(x). При цьому необхідно обов'язково записувати аргумент шуканої функції.

• Для того, щоб вивести в робочий документ значення рішення в будь-якій точці проміжку інтегрування, досить ввести ім'я функції Y, вказати в дужках значення аргументу і знак рівності.

• Значення рішення в будь-якій точці проміжку інтегрування можна використовувати в подальших обчисленнях, досить ввести в потрібному місці ім'я функції Y, вказавши в дужках значення аргументу.

Повну інформацію про правила використання функції odesolve можна отримати у вбудованому довіднику Mathcad в розділі Overview fnd Tutorials.

Приклад 1.

Знайти за допомогою функції odesolve на відрізку 0, 4 рішення задачі Коші

Перш, ніж вводити диференціальне рівняння, вводимо ключове слово Given, а потім диференціальне рівняння.

При введенні диференціального рівняння необхідно в дужках вказати аргумент шуканого рішення і використовувати знак символьної рівності. Потім за рівнянням необхідно ввести початкові умови. При введенні початкової умови, як і при введенні рівняння слід використовувати знак символьної рівності.

	Знак символьної рівності можна ввести з панелі Evalution. Знак символьної рівності можна ввести з клавіатури, натиснув одночасно клавіші <Ctrl>+<=> В результаті змінній y присвоюється значення чисельного рішення задачі Коші на відрізку 0, 4
Побудуємо графік знайденого рішення
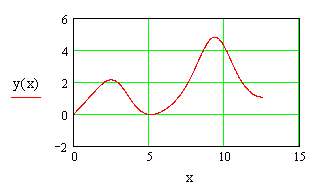
	Для того, щоб побудувати графік рішення y(х), необхідно клацнути в панелі Graph по піктограмі декартового графіка, ввести у відмічених позиціях імена аргументу і функції та клацнути по вільному місці в робочому документі поза виділеної рамки.

Приклад 2. Знайти за допомогою функції odesolve на відрізку 0, 4 рішення граничної задачі

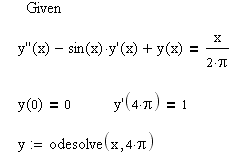
	Знак символьної рівності можна ввести з панелі Evalution. Знак символьної рівності можна ввести з клавіатури, натиснув одночасно клавіші <Ctrl>+<=> В результаті змінній y присвоюється значення чисельного рішення задачі Коші на відрізку 0, 4
Побудуємо графік знайденого рішення
	Для того, щоб побудувати графік рішення y(х), необхідно клацнути в панелі Graph по піктограмі декартового графіка, ввести у відмічених позиціях імена аргументу і функції та клацнути по вільному місці в робочому документі поза виділеної рамки.

Функції для розв’язання систем, записаних в нормальній формі

Вбудовані функції Mathcad, призначені для розв’язання задачі Коші і граничних задач, вирішують їх для нормальних систем звичайних диференціальних рівнянь. Задачі для рівнянь вищих порядків зводяться до відповідних задач для нормальних систем.

Розглянемо завдання Коші:

Чисельне рішення цієї задачі полягає в побудові таблиці наближених значень y_i,1, y_i,2,..., y_i,N рішення y₁(x), y₂(x),..., y_N(x) на відрізку [x₀, x_N] в точках x₁, x₂,..., x_N, які називаються вузлами сітки. Позначивши

, ,

,

,

де - шукане рішення, - вектор початкових умов, а - вектор правих частин, запишемо систему диференціальних рівнянь у векторній формі:

У Mathcad вирішити задачу Коші для такої системи можна за допомогою наступних функцій:

• rkfixed(y, x1, x2, npoints, D) - рішення задачі на відрізку методом Рунге - Кутта з постійним кроком;

• Rkadapt(y, x1, x2, npoints, D) - рішення задачі на відрізку методом Рунге - Кутта з автоматичним вибором кроку;

• rkadapt(y, x1, x2, acc, npoints, D, kmax, save) - рішення задачі в заданій точці методом Рунге - Кутта з автоматичним вибором кроку;

• Bulstoer(y, x1, x2, npoints, D) - рішення задачі на відрізку методом Булірша - Штера;

• bulstoer(y, x1, x2, acc, npoints, D, kmax, save) - рішення задачі в заданій точці методом Булірша - Штера;

• Stiffr(y, x1, x2, acc, D, J) - рішення задачі для жорстких систем на відрізку з використанням алгоритму Розенброка;

• stiffr(y, x1, x2, acc, D, J, kmax, save) - рішення задачі для жорстких систем в заданій точці з використанням алгоритму Розенброка;

• Stiffb(y, x1, x2, acc, D, J) - рішення задачі для жорстких систем на відрізку з використанням алгоритму Булірша - Штера;

• stiffb(y, x1, x2, acc, D, J, kmax, save) - рішення задачі для жорстких систем в заданій точці з використанням алгоритму Булірша - Штера.

Смисл параметрів для всіх функцій однаковий і визначається математичною постановкою задачі:

y - вектор початкових умов

x1, x2 - початкова і кінцева точки відрізку інтегрування системи; для функцій, що обчислюють рішення в заданій точці, x1 - початкова точка, x2 - задана точка;

npoints - число вузлів на відрізку [x1, x]; при рішенні задачі на відрізку результат містить npoints+1 рядок;

D - ім'я вектор-функції D(x, y) правих частин ,D_i(x, y) = f_i(x, y₁,…,y_n); (ім'я D - від Derivative - похідна, ім'я вектора, що містить вирази для похідних (derivatives) шуканого рішення);

J — ім'я матриці-функції J(x, y) розмірності n x (n+1), в першому стовпці якої зберігаються вирази часткових похідних по x правих частин системи, а в решті n стовпців міститься матриця Якобі правих частин:

.

acc - параметр, який контролює похибку рішення при автоматичному виборі кроку інтегрування (якщо похибка рішення більше acc, то крок сітки зменшується; крок зменшується до тих пір, поки його значення не стане менше save);

kmax - максимальне число вузлів сітки, в яких може бути обчислене рішення задачі на відрізку, максимальне число рядків в результаті;

save - найменше допустиме значення кроку нерівномірної сітки.

Результат роботи функції - матриця, перший стовпець якої містить координати вузлів сітки, другий стовпець - обчислені наближені значення рішення y₁(x) у вузлах сітки, (k+1)-ий, - значення рішення y_k(x) у вузлах сітки.

При рішенні задачі Коші для диференціального рівняння першого порядку результат обчислень всіх приведених вище функцій — матриця, в першому стовпці якої містяться координати вузлів сітки x₀, x₁,...,x_N, а в другому — значення наближеного рішення у відповідних вузлах.

Приклад 3. Рішення задачі Коші для звичайного диференціального рівняння І – го порядку з допомогою функції rkfixed.

Знайти на відрізку 0,  наближене рішення рівняння y = sin(xy), яке задовольняє початковим умовам y(0) = 1 і побудувати графік знайденого рішення.

Задачу розв’язати чисельно, використовуючи алгоритм Рунге-Кутта з фіксованим кроком на сітці з 20 рівновіддалених вузлів.

Перш, ніж вводити диференціальне рівняння, визначимо номер першої компоненти вектора 1 (а не нуль, як передбачається по замовченню).

	Ключове слово ORIGIN обов’язково писати прописними літерами
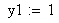
	Вважаючи, що рішення – це вектор з однією компонентою, вводимо початкову умову
	Отримаємо праву частину рівняння – матрицю D(x, y), яка в даному випадку містить один елемент – праву частину рівняння. Тут х – незалежна змінна, у – вектор з єдиною компонентою у1
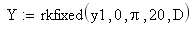
	В результаті матриця Y містить рішення: в першому її стовпці значення х, а в другому – відповідні значення наближеного рішення
Виводимо знайдене наближене рішення в робочий документ
	Для того, щоб вивести в робочий документ матрицю Y, необхідно ввести з клавіатуру ім’я матриці Y і знак рівності
Будуємо графік знайденого рішення у(х)
	Для того, щоб побудувати графік рішення y(х), необхідно клацнути в панелі Graph по піктограмі декартового графіка, ввести у відмічених позиціях імена аргументу (перший стовпець матриці Y) і функції (другий стовпець матриці Y) та клацнути по вільному місці в робочому документі поза виділеної рамки.

Приклад 4. Знайти на відрізку 0, 3 наближене рішення рівняння y = exp(-xy), яке задовольняє початковим умовам y(0) = 1, y(0) = 1 і побудувати графік знайденого рішення.

Зводимо рішення задачі для рівняння другого порядку до задачі для еквівалентної нормальної системи другого порядку. Позначимо

y₁ = y(x), y₂ = y(x);

Оскільки y(х) = (y(x)) = y₂(x), то отримаємо

y1 = y2, y2 = exp(-xy1)

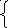y1(0) = 1 y2(0) = 1

Розв’язуємо задачу чисельно, використовуючи алгоритм Рунге-Кутта з фіксованим кроком на сітці з 30 рівновіддалених вузлів.

Перш, ніж вводити диференціальне рівняння, визначимо номер першої компоненти вектора 1, (а не нуль, як передбачається по замовченню).

Приклад 5. Знайти на відрізку 0, 3 наближене рішення задачі Коші

y1 = - y2 + sin(xy3), y2 = - y12 y3 = - y3 – y1,

y1(0) = 1 y2(0) = 0 y3(0) = 1

і побудувати графік знайденого рішення.

Розв’язуємо задачу чисельно, використовуючи алгоритм Рунге-Кутта з фіксованим кроком на сітці з 30 рівновіддалених вузлів.

Приклад 6. Знайти на відрізку 0, 2 наближене рішення задачі Коші

y1 = - 11y1 + 9y2, y2 = 9y1 – 11y2

y1(0) = 1 y2(0) = 0

і побудувати графік знайденого рішення.

Ця система відноситься до класу жорстких систем. Розв’язуємо задачу чисельно на сітці з 20 рівновіддалених вузлів з допомогою функції Stiffr, призначеної для рішення жорстких систем і використовуючи алгоритм Рунге-Кутта. Перед зверненням до функції Stiffr необхідно, крім початкового вектора у і вектора правих частин D(x, y), визначити матрицю J(x, y) розмірністю 23:

	Ключове слово ORIGIN обов’язково писати прописними літерами
	Визначаємо праву частину рівняння – матрицю D(x, y), яка в даному випадку є вектором з двома компонентами (по числу рівнянь в системі). Тут – х – незалежна змінна, у – з компонентами у1 та у2
	Визначаємо матрицю Якобі
	В результаті матриця Y містить рішення: в першому її стовпці значення х, в інших – відповідні значення наближеного рішення
Виводимо знайдене наближене рішення в робочий документ Будуємо графік знайденого рішення у(х).