2.5. Норма квадратної матриці

У лінійній алгебрі використовуються різні матричні норми (norm), які ставлять у відповідність матриці деяку скалярну числову характеристику. Норма матриці відображає порядок величини матричних елементів. У різних специфічних задачах лінійної алгебри застосовуються різні види норм. Mathcad має чотири вбудовані функції для розрахунку різних норм квадратних матриць:

• norm1 (A) — норма в просторі L1;

• norm2 (A) — норма в просторі L2;

• norme(A) — евклідова норма (euclidean norm);

• normi (A) — max-норма, або норма (infinity norm);

  • А — квадратна матриця.

Приклади розрахунку різних норм двох матриць А і В з елементами, що розрізняються на два порядки! наведені в лістингу 30. У останньому рядку цього лістингу дано пояснення евклідової норми, яке схоже на визначення довжини вектора.

У більшості завдань неважливо, яку норму використовувати. Як видно, в звичайних випадках різні норми дають приблизно однакові значення, добре відображаючи порядок величини матричних елементів.

Лістинг 30. Норми матриць

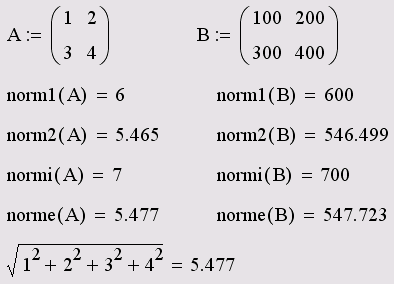
2.6. Число обумовленості квадратної матриці

Ще однією важливою характеристикою матриці є її число обумовленості (condition number). Число обумовленості є мірою чутливості системи лінійних рівнянь A∙B = X, яка визначається матрицею А, до похибки завдання вектора В правих частин рівнянь. Чим більше число обумовленості, тим сильніше цей вплив і тим більше нестійкий процес знаходження рішення. Число обумовленості пов'язане з нормою матриці і обчислюється по-різному для кожної з норм;

• cond1(A) — число обумовленості в нормі L1;

• cond2 (A) — число обумовленості в нормі L2;

• conde(A) — число обумовленості в евклідовій нормі;

• condi (A) — число обумовленості в нормі;

  • А — квадратна матриця.

Розрахунок чисел обумовленості для двох матриць А і В показаний в лістингу 31. Слід звернути увагу, що перша з матриць є добре обумовленою, а друга - погано обумовленою (два її рядки визначають дуже близькі системи рівнянь, з точністю до множника 10³). Другий рядок лістингу дає формальне визначення числа обумовленості як добутки норм початкової і оберненої матриць. У інших нормах визначення таке саме.

Як неважко зрозуміти, матриці А і В з попереднього лістингу 30 володіють однаковими числами обумовленості, оскільки В=100*А, і, отже, обидві матриці визначають одну і ту ж систему рівнянь.

Лістинг 31. Числа обумовленості матриць

2.7. Ранг матриці

Рангом (rank) матриці називають найбільше натуральне число k, для якого існує не рівний нулю визначник k-ro порядку підматриці, складеної з будь-якого перетину k стовпців і k рядків матриці.

Для обчислення рангу в Mathcad призначена функція rank.

• rank (А) — ранг матриці;

  • А — матриця.

Лістинг 32. Ранг матриці

3. Системи лінійних рівнянь алгебри

Центральним питанням обчислювальної лінійної алгебри є рішення систем лінійних рівнянь алгебри, тобто систем рівнянь вигляду

а_i1x₁+а_i2х₂+. . .+a_inх_n = b_i (1)

У матричній формі система лінійних алгебраїчних рівнянь записується в еквівалентному вигляді:

Ах = b, (2)

де А — матриця коефіцієнтів системи лінійних алгебраїчних рівнянь розмірності NN;

х — вектор невідомих;

b— вектор правих частин рівнянь.

До систем лінійних рівнянь зводиться множина, якщо не сказати більшість, завдань обчислювальної математики.

Система лінійних алгебраїчних рівнянь має єдине рішення, якщо матриця А є невиродженою, або, по-іншому, несингулярною, тобто її визначник не рівний нулю. З обчислювальної точки зору, рішення системи лінійних алгебраїчних рівнянь не представляє труднощів, якщо матриця А не дуже велика. З великою матрицею проблем також не виникне, якщо вона не дуже погано обумовлена. У Mathcad систему лінійних алгебраїчних рівнянь можна вирішити як в наочній формі (1), так і в зручнішій для запису формі (2). Для першого способу слід використовувати обчислювальний блок Given/Find, а для другого — вбудовану функцію lsolve.

• lsolve ( А, b) — рішення системи лінійних рівнянь;

• А — матриця коефіцієнтів системи;

• b — вектор правих частин.

Застосування функції lsolve показане в лістингу 33. При цьому матриця А може бути визначена будь-яким із способів. Вбудовану функцію lsolve допускається застосовувати і при символьному рішенні системb лінійних алгебраїчних рівнянь (лістинг 34).

Відповідна матриці А і вектору b система рівнянь виписана явно в лістингу 35.

Лістинг 33. Рішення системи лінійних алгебраїчних рівнянь

Лістинг 34. Символьне рішення системи лінійних алгебраїчних рівнянь (продовження лістингу 33)

В деяких випадках, для більшої наочності представлення системи лінійних алгебраїчних рівнянь, її можна вирішити точно так, як і систему нелінійних рівнянь. Приклад чисельного рішення системи лінійних алгебраїчних рівнянь показаний в лістингу 35. При чисельному рішенні всім невідомим потрібно привласнити початкові значення (це зроблено в першому рядку лістингу 35). Вони можуть бути довільними, оскільки рішення системи лінійних алгебраїчних рівнянь з невиродженою матрицею єдино.

При рішенні системи лінійних алгебраїчних рівнянь за допомогою функції Find Mathcad автоматично вибирає лінійний чисельний алгоритм, в чому можна переконатися, викликаючи на імені Find контекстне меню.

Лістинг 35. Рішення системи лінійних алгебраїчних рівнянь за допомогою обчислювального блоку