1.3. Множення

При множенні слід пам'ятати, що матрицю розмірності MN допустимо умножати тільки на матрицю розмірності NP (Р може бути будь-яким). В результаті виходить матриця розмірності МР.

Щоб ввести символ множення, потрібно натиснути клавішу із зірочкою <*> або скористатися панеллю інструментів Matrix (Матриця), натиснувши на ній кнопку Dot Product (Множення) (рис. 1). Множення матриць позначається за умовчанням крапкою, як показано в лістингу 5. Символ множення матриць можна вибирати точно так, як і в скалярних виразах.

Лістинг 5. Множення матриць

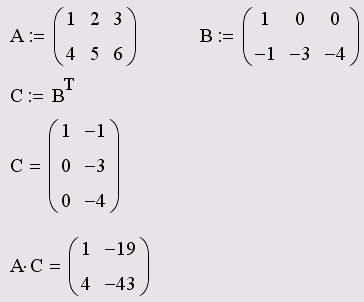
Ще один приклад, що відноситься до множення вектора на матрицю-рядок і, навпаки, рядки на вектор, приведений в лістингу 6. У другому рядку цього лістингу показано, як виглядає формула при виборі відображення оператора множення No Space (Разом).

Лістинг 6. Множення вектора і рядка

Той же самий оператор множення діє на два вектори по-іншому.

Аналогічно додаванню матриць з скаляром визначається множення і ділення матриці на скалярну величину (лістинг 7). Символ множення вводиться так само, як і у разі множення двох матриць. На скаляр можна умножати будь-яку матрицю MN.

Лістинг 7. Множення матриці на скаляр

1.4. Визначник квадратної матриці

Визначник (Determinant) матриці позначається стандартним математичним символом. Щоб ввести оператора знаходження визначника матриці можна натиснути кнопку Determinant (Визначник) на панелі інструментів Matrix (Матриця) (рис. 2) або набрати на клавіатурі <|> (натиснувши клавіші <Shift>+<\>). В результаті будь-якої з цих дій з'являється месцезаповнювач, в який слід помістити матрицю. Щоб обчислити визначника вже введеної матриці (саме цей випадок показаний на рис. 2), потрібно:

• Перемістити курсор в документі так, щоб помістити матрицю між лініями введення (нагадуємо, що лінії введення — це вертикальний і горизонтальний відрізки синього кольору, створюючи куточок, який вказує на поточну область редагування).

• Ввести оператора знаходження визначника матриці.

• Ввести знак рівності, щоб обчислити визначника.

Рис. 2 Введення символу визначника матриці

Результат обчислення визначника приведений в лістингу 8.

Лістинг 8. Пошук визначника квадратної матриці

1.5. Модуль вектора

Модуль вектора (vector magnitude) позначається тим же символом, що і визначник матриці. За визначенням, модуль вектора рівний квадратному кореню з суми квадратів його елементів (лістинг 9).

Лістинг 9. Пошук модуля вектора

1.6. Скалярний добуток векторів

Скалярний добуток векторів (vector inner product) визначається як скаляр, рівний сумі попарних добутків відповідних елементів.

Вектори повинні мати однакову розмірність, скалярний добуток має ту ж розмірність. Скалярний добуток двох векторів u і v рівний u∙v = |u|∙|v|∙cosQ, де Q - кут між векторами. Якщо вектори ортогональні, їх скалярний добуток рівний нулю. Позначається скалярний добуток тим же символом множення (лістинг 10). Для позначення скалярного добутку також можна вибирати представлення * оператора множення.

Ніколи не слід застосовувати для позначення скалярного добутку символ , який є загальновживаним символом векторного добутку.

Лістинг 10. Скалярний добуток векторів

Уважно слід перемножувати декілька (більше двох) векторів. По-різному розставлені дужки повністю змінюють результат множення. Приклади такого множення наведені в лістингу 11.

Лістинг 11. Скалярний добуток векторів, помножений на третій вектор