
ТМБ, част1 / Конспект / ТМБ1_Лекц_я 06_Статистичнi методи дослiдження якостi виробiв.:.pdf
.pdf
6. СТАТИСТИЧНІ МЕТОДИ ДОСЛІДЖЕННЯ ЯКОСТІ ВИРОБІВ
1.Головні числові характеристики випадкових величин.
2.Головні закони розподілу випадкових величин та їх властивості.
3.Застосування теорії ймовірностей та математичної статистики для розв'язування задач технології машинобудування
4.Статистичний контроль у машинобудуванні.
Точність оброблення, як один з основних показників якості виробу, залежить від ряду фак- торів (див. розділ 2). Кожен з них здійснює різний вплив на точність. Причому похибки, які вини- кають від їх дії, у кожному конкретному випадку можуть або сумуватися, або взаємно погашатися.
Основною вимогою, яка висувається до технологічного процесу, є забезпечення заданої то- чності виготовлення деталі. Тому при проектуванні технологічного процесу необхідно знати, яку точність забезпечують ті чи інші методи оброблення.
Існують два методи розрахунку точності.
А н а л і т и ч н и й м е т о д вимагає дослідження всіх первинних похибок оброблення Через свою складність його використовують лише в окремих випадках1. Окрім цього, при використанні цього методу неможливо з практичною точністю врахувати випадкові похибки оброблення.
С т а т и с т и ч н и й м е т о д базується на теорії ймовірності і математичній статистиці, які дозволяють встановити закономірність виникнення похибок, як систематичного, так і випадкового характеру.
Випадкові похибки, не дивлячись на їх різноманіття, мають деякі загальні особливості, зок-
рема:
∙незначні похибки зустрічаються частіше, аніж великі;
∙для визначеного способу виготовлення (оброблення) випадкові похибки не перевищують певної величини;
∙різнознакові похибки зустрічаються з однаковою частотою;
∙зі збільшенням кількості деталей у партії середнє арифметичне з випадкових похибок наближається до нуля.
6.1.Головні числові характеристики випадкових величин.
Сукупність випадкових величин можна вважати відомою, коли відомо, яких значень ці ве- личини набувають, а також частоту чи ймовірність їх появи. В і д н о с н о ю ч а с т о т о ю появи пе- вного значення випадкової величини, є відношення
p = |
m |
, |
(6.1) |
|
|||
|
n |
|
|
де m – кількість випадків появи певного значення випадкової величини (абсолютна частота); n – загальна кількість випадків появи всіх можливих значень випадкової величини.
1 Методика аналітичного розрахунку точності наведена у розділі 8 “ Досягнення необхідної якості деталей машин в процесі виготовлення”.
6. Статистичні методи дослідження якості виробів
За достатньо великої кількості вимірювань відносну частоту випадкової величини прийма- ють за с т а т и с т и ч н у й м о в і р н і с т ь або просто й м о в і р н і с т ь .
Приклад 6.1. На налаштованому відрізному верстаті необхідно відрізати 50 заготовок, номі- нальна довжина яких повинна дорівнювати 200 мм.
При вимірюванні довжини кожної заготовки штангенциркулем з точністю вимірювання 0,1 мм виявилося, що з цих 50 заготовок 1 заготовка має довжину 199,8 мм, 2 заготовки – 199,9 мм, 9 заго- товок – 200,0 мм, 24 заготовки – 200,1 мм, 10 заготовок – 200,2 мм, 4 заготовки – 200,3 мм. Відносні частоти появи цих розмірів наведені у табл. 5.1.
Таблиця 6.1.
Відносна частота розмірів партії заготовок
Розмір |
Кількість деталей |
Відносна частота |
|||||||||||||||||||
з розміром l |
|||||||||||||||||||||
заготовки l,мм |
|
розміру l, pi |
|||||||||||||||||||
(абсолютна частота) mi |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
l1 = 199,8 |
m1 = 1 |
p |
= |
|
|
|
|
m1 |
= |
1 |
|
|
= 0,02 |
||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
1 |
|
|
|
|
|
n |
50 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
l2 = 199,9 |
m2 = 2 |
p2 |
= |
|
|
|
|
m2 |
|
|
|
= |
|
|
2 |
|
|
= 0,04 |
|||
|
n |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
50 |
|
|
||||||||||
l3 |
= 200,0 |
m3 = 9 |
p3 |
|
|
|
= |
m3 |
= |
|
9 |
|
= 0,18 |
||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
50 |
|
|
|
||||||||
l4 |
= 200,1 |
m4 = 24 |
p4 |
= |
|
|
m4 |
|
= |
24 |
= 0,48 |
||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
50 |
|
|
|
||||||||
l5 |
= 200,2 |
m5 = 10 |
p5 |
= |
|
m5 |
|
= |
10 |
= 0,20 |
|||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
50 |
|
|
|
||||||||
l6 |
= 200,3 |
m6 = 4 |
p6 |
= |
m6 |
|
= |
4 |
|
|
= 0,08 |
||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
50 |
|
|
|||||||||
|
|
∑mi = 50 |
|
∑pi = 1,00 |
|||||||||||||||||
Коли всі відрізані заготовки покласти в тару і за потребою виймати по одній, то ймовірність взяти заготовку того чи іншого розміру дорівнюватимуть частотам появи цих розмірів при відрізу- ванні заготовок.
Для числової характеристики сукупності випадкових величин найчастіше використовують:
∙середнє значення випадкової величини;
∙розмах випадкової величини;
∙середнє арифметичне відхилення випадкової величини від її середнього значення;
∙дисперсію випадкової величини;
∙середнє квадратичне відхилення випадкової величини від її середнього значення.
С е р е д н є з н а ч е н н я в и п а д к о в о ї в е л и ч и н и , яке в теорії ймовірності називається також м а т е м а т и ч н и м с п о д і в а н н я м , знаходять як середнє арифметичне значення суми всіх випадкових величин. Для партії з n деталей це значення рівне:
|
|
|
l1m1 + l2m2 + ... + ln mn |
|
|
|
|
|
|
n |
|
|
|
|
l |
cр |
= |
= l |
p |
+ l |
m |
2 |
+ ... + l |
m = ∑l |
p |
i |
(6.2) |
||
|
||||||||||||||
|
|
n |
1 |
1 |
2 |
|
n |
i |
|
|
||||
|
|
|
|
|
|
|
|
|
i =1 |
|
|
|
Місце, яке займає кожна конкретна випадкова величина у межах всієї сукупності величин, можна визначити в і д х и л е н н я м ц і є ї в е л и ч и н и в і д с е р е д н ь о г о з н а ч е н н я сукупнос- ті:
i = li − lcр |
(6.3) |
2

6. Статистичні методи дослідження якості виробів
Оскільки у загальній сукупності одна частина випадкових величин більша, а інша – менша за середнє значення, то і їх відхилення від середнього значення для однієї частини будуть додат- ними, а для іншої – від’ємними. Середнє значення всіх додатних відхилень, як і середнє значення всіх від’ємних відхилень, дає додаткову інформацію про розподіл випадкових величин. Очевидно, що замість двох середніх значень відхилень як характеристику зручніше мати одне загальне серед- нє значення. Але, оскільки середнє значення всіх відхилень рівне нулю, то у цьому випадку необ- хідно брати або середнє з абсолютних значень усіх відхилень, або середнє значення всіх квадратів відхилень.
У першому випадку дістають с е р е д н є |
з у с і х а б с о л ю т н и х |
з н а ч е н ь : |
|
||||||||||||||||||||||||||||||||||
h = |
|
( l1 − lcр ) |
|
m1 + |
|
( l2 − lcр ) |
|
m2 + ... + |
|
( ln − lср ) |
|
mn = ∑( li − lcр ) pi |
(6.4) |
||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
i =1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
У другому випадку отримують дещо іншу характеристику, яку прийнято називати д и с п е - |
|||||||||||||||||||||||||||||||||||||
р с і є ю в и п а д к о в о ї в е л и ч и н и : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
n |
|
|
|
|
|
||||||
D( l ) = |
( l1 − lcр ) |
m1 + ( l2 − lcр ) |
|
m2 + ... + ( ln − lср ) |
|
mn |
= |
|
|
− lcр )2 pi |
(6.5) |
||||||||||||||||||||||||||
|
|
∑( li |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Квадратний корінь з дисперсії: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i =1 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
− l |
|
)2 m |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑( l |
i |
cр |
i |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
σ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i =1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
∑( li − lcр )2 pi = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.6) |
||||||||
|
|
|
|
|
|
|
|
|
D( l ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
є однією з найважливіших характеристик сукупностей випадкових величин – |
|
с е р е д н є |
к в а д р а - |
||||||||||||||||||||||||||||||||||
т и ч н е в і д х и л е н н я в и п а д к о в и х |
в е л и ч и н в і д ї х |
|
с е р е д н ь о г о |
|
з н а ч е н н я . Диспер- |
||||||||||||||||||||||||||||||||
сія, середнє та середнє квадратичне відхилення випадкових величин від їх середнього значення ха- рактеризують до деякої міри розсіювання випадкової величини, повний діапазон (р о з м а х ) якого виражається різницею між найбільшим та найменшим її значенням:
|
|
|
|
|
R = lmax − lmin |
|
(6.7) |
|
|||
|
Для вищенаведеного прикладу 1, числові характеристики сукупності випадкових величин, |
||||||||||
якими є довжина відрізання, а також порядок їх розрахунку зведені у табл. 6.2. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
Таблиця 6.2. |
|
|
|
Числові характеристики та порядок їх розрахунку (за даними прикладу 1) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
li , мм |
m1 |
li mi , мм |
pi |
li − lcр |
|
( li − lcр ) |
mi |
( li − lcр )2 |
( li − lcр )2 mi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
199,8 |
1 |
199,8 |
0,02 |
-0,304 |
|
0,304 |
|
0,0924 |
0,0924 |
|
|
199,9 |
2 |
399,8 |
0,04 |
-0,204 |
|
0,408 |
|
0,0416 |
0,0832 |
|
|
200,0 |
9 |
1 800,0 |
0,18 |
-0,104 |
|
0,936 |
|
0,0108 |
0,0972 |
|
|
200,1 |
24 |
4802,4 |
0,48 |
-0,004 |
|
0,096 |
|
0,0000 |
0,0000 |
|
|
200,2 |
10 |
2 002,0 |
0,20 |
+0,096 |
|
0,960 |
|
0,0020 |
0,0020 |
|
|
200,3 |
4 |
801,2 |
0,08 |
+0,196 |
|
0,784 |
|
0,0384 |
0,1536 |
|
|
Разом: |
50 |
10 005,2 |
1,00 |
--- |
|
3,488 |
|
---- |
0,4284 |
|
lcр |
= ∑ |
li mi |
|
= |
10 005,2 |
= 200,104 мм; |
||||||||
n |
|
|
|
|||||||||||
|
|
|
|
|
50 |
|
|
|
||||||
h = |
∑ |
|
( li − lcр ) |
|
mi |
= |
3,488 |
= 0,09676 |
||||||
|
|
|||||||||||||
|
|
|
n |
|
|
|
|
50 |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
3

6. Статистичні методи дослідження якості виробів
|
∑ |
( l |
i |
− l |
cр |
) |
|
2m |
||||||
D( l ) = |
|
|
|
|
|
|
|
i |
= |
0,4284 |
= 0,0086 |
|||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
n |
|
|
|
|
||||||
|
|
|
|
|
|
50 |
|
|||||||
σ = |
|
|
= |
|
|
|
= 0,093 мм |
|||||||
|
D( l ) |
|
0,0086 |
|||||||||||
При розв’язуванні деяких технологічних задач доводиться часто визначати числові характе- ристики не для окремих випадкових величин, а для їх суми або добутку. У цьому випадку не обхі- дно використовувати теореми про середні значення і дисперсії сум і добутків випадкових величин.
Середнє значення суми випадкових величин дорівнює сумі середніх значень цих величин:
X cр ( x1 + x2 + ... + xn ) = x1cр + x2cр + ... + xncр |
(6.8) |
Аналогічно, середнє значення добутку випадкових величин дорівнює добутку їх середніх значень:
X cр ( x1 x2 ... xn ) = x1cр x2cр ... xncр |
(6.9) |
Дисперсія суми випадкових величин дорівнює сумі дисперсій цих величин: |
|
D( x1 + x2 + ... + xn ) = D( x1 ) + D( x2 ) + ... + D( xn ) |
(6.10) |
Дисперсія суми випадкової і постійної величин дорівнює дисперсії випадкової величини:
D( c + x ) = D( x ) |
(6.11) |
Дисперсія добутку постійної і випадкової величин дорівнює добутку квадрата постійної ве- личини і дисперсії випадкової величини:
D( cx ) = c2 D( x ) |
(6.12) |
Дисперсія добутку двох випадкових величин дорівнює добутку дисперсій цих величин, збі- льшеному на суму добутків дисперсії однієї величини і квадрата середнього значення другої:
D( xy ) = D( x )D( y ) + D( x ) yc |
2 + D( y )xc |
2 |
(6.13) |
6.2. Головні закони розподілу випадкових величин та їх властивості.
6.2.1. Способи вираження законів розподілу випадкових величин.
Кожна з описаних у п. 6.1 числових характеристик несе ту чи іншу інформацію про сукуп- ність випадкових величин, проте не дає повного уявлення про цю сукупність, тобто не дає відпові- ді на питання, з якими частотами з’являються ці чи інші значення випадкових величин. Повне уяв- лення про будь-яку сукупність випадкових величин може дати лише знання з а к о н у р о з п о д і - л у , якому підпорядковується ця сукупність.
Закон розподілу, як довільну математичну функцію, можна виразити одним з трьох основ- них способів: у вигляді числової таблиці, графіка або математичної функції. Зокрема, для прикла- ду 1, закон розподілу розмірів заготовок можна виразити числовою таблицею (див. табл. 6.1). За даними числової таблиці закон розподілу виражають графічно у вигляді г і с т о г р а м и , побудова- ної з прямокутників, які відповідають частотам окремих діапазонів значень випадкової величини або емпіричною кривою розподілу – п о л і г о н о м або м н о г о к у т н и к о м р о з п о д і л у . Для по- будови таких графіків на осі абсцис відкладають значення випадкової величини (поле розсіювання розмірів чи поле допуску, поділене на прийняту кількість інтервалів), а на осі ординат – абсолютні або відносні частоти, які відповідають її значенням (рис. 6.1, 6.2). Після з’єднання точок отриму- ють ламану лінію. При збільшенні кількості деталей у партії ламана лінія наближається до плавної кривої – к р и в о ї р о з п о д і л у .
За невеликої кількості деталей у партії побудову кривої ведуть безпосередньо за отримани- ми розмірами деталей. Для великих партій різницю між найбільшим і найменшим фактичними розмірами виміряних деталей розподіляють на рівні інтервали й визначають кількість деталей,
4

6. Статистичні методи дослідження якості виробів
розміри яких знаходяться у межах певного інтервалу. Збільшення кількості деталей у партії на- ближає ламану лінію до плавної кривої.
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.1. Гістограма і полігон розподілу |
Рис. 6.2. Гістограма і полігон розподілу |
||||
абсолютних частот випадкових величин. |
відносних частот випадкових величин. |
||||
Розміри деталей, які отримують у процесі оброблення – це безперервні випадкові величини. Проводячи вимірювання за допомогою приладу обмеженої точності, отримують дискретні значен- ня випадкових величин. Насправді відповідні частоти цих величин відповідають не їх абсолютним значенням, а діапазонам значень. Наприклад, розмір 200,1 мм, відрахований на штангенциркулі з точністю 0,1 мм, ще не свідчить про те, що абсолютна довжина заготовки складає 200,100 мм. До цього розміру зараховують, очевидно, всі заготовки, розміри яких знаходяться в діапазоні від 200,05 до 200,15 мм. Таким чином, кожний прямокутник на гістограмі відповідає своєму діапазону розмірів випадкової величини, а поверхня такого прямокутника відображає відносну частоту роз- мірів у цьому діапазоні. Оскільки сума відносних частот випадкової величини для всієї їх сукупно- сті рівна одиниці, то й всю площу гістограми можна вважати за одиницю.
Якщо полігон розподілу випадкової величини апроксимувати математичною кривою, то рі- вняння цієї кривої буде математичним виразом закону розподілу для сукупності випадкових вели- чин. Як і для полігону розподілу, вся площа кривої дорівнюватиме одиниці, тобто
+∞ |
|
∫ ydx = 1 |
(6.14) |
−∞
Утеорії ймовірностей використовують багато математичних функцій, які виражають закони розподілу. У найпростіших випадках ці функції зображують прямою лінією чи найпростішою ком- бінацією прямих.
Прикладом таких законів розподілу є з а к о н р і в н о ї й м о в і р н о с т і , який виражається горизонтальною прямою y=const і свідчить про те, що в певному діапазоні значень випадкової ве- личини (між мінімальним і максимальним її значенням), імовірність появи будь-якого значення є постійною (рис. 6.3, а). Прикладом простих законів розподілу є також закон розподілу випадкової величини по трикутнику – з а к о н С і м п с о н а (рис. 6.3, б). Найбільш ж розповсюдженим у науці і техніці є так званий н о р м а л ь н и й з а к о н р о з п о д і л у випадкових величин – закон Гауса
(рис. 6.3, в).
5

6. Статистичні методи дослідження якості виробів
а) б) в)
Рис. 6.3. Головні закони розподілу випадкових величин у технології машинобудування а) закон рівної ймовірності; б) закон Сімпсона (закон трикутника);
в) закон Гауса (нормальний закон).
6.2.2. Нормальний закон розподілу випадкових величин (закон Гауса) і його основні властивості.
Закон Гауса має теоретичне обґрунтування і підтверджується практикою. Закон Гауса свід- чить про те, що більшість значень випадкових величин у науці і в техніці (зокрема й розміри дета- лей машин, які підлягають механічному обробленню) групується за середніми значеннями цих ве- личин. Зі зростанням відхилень випадкових величин від їх середнього значення, частота появи цих величин швидко зменшується, наближаючись до нуля. Ця закономірність виражається показнико- вою функцією:
|
|
1 |
|
− |
x 2 |
|
|
|
|
|
|
|
|||
y = |
|
|
e 2σ 2 |
(6.15) |
|||
|
|
|
|
||||
σ |
|
2π |
|||||
|
|
|
|
|
|
||
де y – частота появи аргумента (випадкової величини); σ – |
середнє квадратичне значення аргумен- |
||||||
та (див. (6.6)); е = 2,718 – базис (основа) натурального логарифма; x – відхилення дійсних розмірів від середніх, яке рівне різниці розміру кожної деталі і середньоарифметичного розміру партії
( x = i = li − lcр (див. (6.3)).
Формула (6.15) виражає нормальний закон розподілу в прямокутній системі координат, по- чаток якої відповідає нульовому значенню випадкової величини.
Як видно з наведених формул і їх графічного зображення, функція, яка виражає нормальний закон розподілу, є симетричною показниковою функцією, максимум якої знаходиться при х = 0 і дорівнює
ymax = |
|
1 |
|
= 0,3989 |
1 |
≈ 0,4 |
1 |
(6.16) |
|
|
|
|
|
σ |
σ |
||||
σ |
|
2π |
|||||||
|
|
|
|
|
|
||||
При всіх інших значеннях аргументу (як додатних, так і від'ємних):
− x 2
e 2σ 2 < 1 ,
тобто, значення функції завжди будуть меншими за максимальні. Зі зростанням величини х до не- скінченості, значення функції (6.15) асимптоматично наближатиметься до нуля. Наприклад, для
|
− |
x 2 |
|
|
|
|
|
|
|
|
значень аргументу х = ±1 σ, ±2 σ, ±3 σ, значення e |
2σ 2 |
відповідно дорівнюватимуть 0,6065; 0,1353; |
||||||||
|
||||||||||
0,0111, а значення функції у, які їм відповідають – |
|
y1σ = 0,243 |
1 |
; y2σ = 0,053 |
1 |
; y3σ = 0,0044 |
1 |
. |
||
|
σ |
σ |
σ |
|||||||
6

6. Статистичні методи дослідження якості виробів
З рівняння кривої нормального розподілу слідує, що середнє квадратичне відхилення є єди- ним параметром, яке визначає форму кривої нормального розподілу. На рис. 5.4 показано криві нормального розподілу, ординати яких визначені при σ = 0,5; 1,0; 2,0. Форма кривих дозволяє зро- бити висновок про те, що чим менша величина σ, тим менше крива розтягнена і, як наслідок, мен- ше розсіювання розмірів. Таким чином, величина σ визначає розсіювання розмірів і характеризує ступінь впливу випадкових похибок.
Рис. 6.4. Криві нормального розподілу випадкових величин при різних значеннях середнього квадратичного відхилення(σ = 0,5; 1,0; 2,0)
На основі досліджень встановлено, що в інтервалі x = ±0,36σ знаходиться 35% усіх розмі- рів оброблених розмірів, при x = ±0,76σ – 50%, а при x = ±0,36σ – 99,7%. В останньому випадку крива нормального розподілу практично зливається з віссю абсцис, тобто відхилення дійсних роз- мірів від середнього розміру практично всіх оброблених деталей знаходяться у межах ± 3σ або, за абсолютною величиною, – 6σ . Звідси можна зробити висновок, що якщо допуск δ на оброблення заготовок більший за 6σ , то точність процесу відповідає необхідним вимогам. Якщо ж допуск δ на оброблення є менший за 6σ . То частина деталей не відповідатиме витримуваному розміру.
Таким чином, дослідження точності технологічної операції за допомогою методів матема- тичної статистики дозволяє:
∙визначити точність виготовлення на операції (при цьому основним критерієм точності є умова δ ³ 6σ );
∙визначити ймовірність отримання кількості деталей з розмірами в інтервалах допуску; для цього визначають відносну частоту (ймовірність) випадків y’ шляхом ділення абсолютної час- тоти на кількість деталей у партії:
y' = |
y |
або y' = |
100 y |
, |
N |
|
|||
|
|
N |
||
де y – абсолютна частота випадків; N – кількість деталей у партії.
При побудові теоретичної кривої нормального розподілу, її необхідно звести до масштабу, в якому побудована гістограма (чи полігон розподілу). Для цього слід значення ординат (тобто зна- чення функції, визначених за табл. 6.2), помножити на величину прийнятого інтервалу розмірів:
l = li −1 − li |
(6.17) |
Приклад гістограми, полігону розподілу та теоретичної кривої розподілу, побудованих за даними табл. 6.2, показаний на рис. 6.5. Для цього прикладу, при прийнятому інтервалі розмірів
7

6. Статистичні методи дослідження якості виробів
l = li −1 - li = 0,1 мм, ординати для найбільш характерних точок теоретичної кривої дорівнювати- муть:
ymax = 0,40 |
1 |
|
l = 0,40 |
|
1 |
× 0,1 = 0,430 ; |
|
y1σ = 0,242 |
1 |
|
l = 0,242 |
|
1 |
|
× 0,1 = 0,258 ; |
|||||||
σ |
|
0,093 |
|
σ |
|
0,093 |
|
|||||||||||||||
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|
|||||
y2σ = 0,053 |
|
|
|
l = 0,053 |
|
× 0,1 = 0,058 |
; |
y3σ = 0,0044 |
|
l = 0,0044 |
|
|
× 0,1 = 0,0047 . |
|||||||||
|
σ |
|
0,093 |
σ |
0,093 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.5. Гістограма, полігон та теоретична крива розподілу випадкових величин за даними табл. 5.2 (σ = 0,093 мм)
Як видно з наведених даних, для x = 3σ значення функції у дорівнює » 0,01ymax , тобто фа-
ктично сягає нуля. Це означає, що весь діапазон розподілу значень випадкової величини, який від- повідає нормальному закону, дорівнює практично
τ ≈ 6σ |
(6.18) |
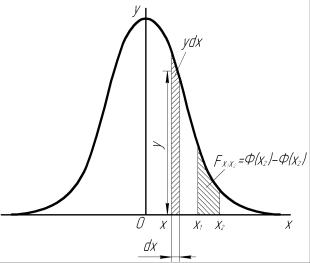
До цього ж висновку можна дійти, визначаючи площі кривої для різних значень аргументу, тобто знаходячи інтеграл функції (6.15). Коли розглядати криву розподілу Гауса, як будь-яку іншу криву розподілу, то ймовірність того, що серед різних значень випадкової величини будуть зна- чення в діапазоні від х до х+dx, дорівнюватиме площі ydx (рис. 6.6).
Таким чином, для довільного діапазону (від х1 до х2) площа кривої, очевидно, виражати- меться інтегралом:
x2 |
x2 |
|
|
1 |
|
|
|
|
− |
|
x 2 |
|
|
|
|
|
||
|
|
|
|
|
|
2 |
|
|
|
|
||||||||
F = ∫ ydx = |
∫ |
|
|
|
|
|
e 2σ |
dx , |
|
(6.19) |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
σ |
|
2π |
|
|
|
|||||||||||||
x1 |
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
а для всієї кривої: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ ∞ |
+ ∞ |
|
1 |
|
|
|
− |
x 2 |
|
|
|
|
||||||
|
|
|
|
2σ |
2 |
|
|
|
||||||||||
F = ∫ ydx = |
∫ |
|
|
|
|
|
e |
dx |
= 1 , |
(6.20) |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
σ |
|
|
2π |
|
|
|
|
||||||||||
−∞ |
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
8
6. Статистичні методи дослідження якості виробів
Рис. 6.6. Імовірності появи випадкових величин для заданих діапазонів їх значень при нормальному законі розподілу
Оскільки таким інтегралом доводиться часто користуватися, то для того, щоб не повторю- вати розрахунки кожен раз, складено таблиці, в яких замість аргументу х введено нову змінну
z = |
x |
(6.21) |
σ |
Така підстановка дає змогу усунути з формули параметр σ, оскільки
dz = |
dx |
і dx = σ dz |
(6.22) |
|
σ |
||||
|
|
|
Підставляючи в підінтегральне значення dx = σ dz та скорочуючи його на σ, отримують но- вий інтеграл, який називають і н т е г р а л о м Г а у с а . Значення інтеграла Гауса для різних значень аргументу z наведено в табл. 6.3.
Як видно з табл. 6.3, половина площі кривої Гауса дорівнює 0,5 (вся площа – одиниці), а для z = 3 , тобто для інтервалу значень випадкової величини від -3 до +3, поверхня кривої дорівнює 0,49865 × 2 = 0,9973. Іншими словами, в інтервалі ±3 σ знаходиться 99,73% всієї площі кривої Гауса, що підтверджує (5.18).
Використовуючи таблицю значень інтеграла Гауса, можна визначити ймовірність появи ви- падкової величини для довільного інтервалу її значень від -3σ до +3σ.
6.2.3. Інші закони розподілу випадкових величин і їх властивості.
Як вже було сказано вище, окрім нормального закону розподілу випадкових величин, у тех- нології машинобудування доволі часто використовують закон рівної ймовірності та закон Сімпсо- на (див. рис. 6.3).
Відповідно до (6.5) величину дисперсії для будь-якої дискретної випадкової величини х у загальному вигляді можна виразити формулою:
|
|
|
|
|
|
n |
|
2 |
mi |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
D(x) = |
∑(xi − x cр ) |
|
|
|
|
|
|
|
|
|
|
(6.23) |
||||
|
|
|
|
n |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|||
Піднімаючи вираз у дужках до квадрату, формулу (6.23) перетворюється у вид: |
|
||||||||||||||||||
n |
2 |
|
|
m |
i |
n |
2 |
m |
i |
|
|
m |
i |
|
2 |
m |
i |
|
|
D(x) = ∑(xi |
− 2xi x cр |
+ 2x cр2 ) |
|
= ∑ xi |
|
− 2xi x cр |
|
+ 2x cр |
|
|
(6.24) |
||||||||
|
n |
|
|
n |
|
n |
|
|
|
|
|||||||||
i=1 |
|
|
|
|
i=1 |
|
|
|
|
|
|
|
n |
|
|||||
9
6. Статистичні методи дослідження якості виробів
Таблиця 6.3.
Значення інтеграла Гауса
z |
Ф (z) |
z |
Ф (z) |
z |
Ф (z) |
z |
Ф (z) |
0,00 |
0,0000 |
|
|
|
|
|
|
0,01 |
0,0040 |
0,31 |
0,1217 |
0,72 |
0,2642 |
1,80 |
0,4641 |
0,02 |
0,0080 |
0,32 |
0,1255 |
0,74 |
0,2703 |
1,85 |
0,4678 |
0,03 |
0,0120 |
0,33 |
0,1293 |
0,76 |
0,2764 |
1,90 |
0,4713 |
0,04 |
0,0160 |
0,34 |
0,1331 |
0,78 |
0,2823 |
1,95 |
0,4744 |
0,05 |
0,0199 |
0,35 |
0,1368 |
0,80 |
0,2881 |
2,00 |
0,4772 |
0,06 |
0,0239 |
0,36 |
0,1406 |
0,82 |
0,2939 |
2,10 |
0,4821 |
0,07 |
0,0279 |
0,37 |
0,1443 |
0,84 |
0,2995 |
2,20 |
0,4861 |
0,08 |
0,0319 |
0,38 |
0,1480 |
0,86 |
0,3051 |
2,30 |
0,4893 |
0,09 |
0,0359 |
0,39 |
0,1517 |
0,88 |
0,3106 |
2,40 |
0,4918 |
0,10 |
0,0398 |
0,40 |
0,1554 |
0,90 |
0,3159 |
2,50 |
0,4938 |
0,11 |
0,0408 |
0,41 |
0,1591 |
0,92 |
0,3212 |
2,60 |
0,4953 |
0,12 |
0,0478 |
0,42 |
0,1628 |
0,94 |
0,3264 |
2,70 |
0,4965 |
0,13 |
0,0517 |
0,43 |
0,1664 |
0,96 |
0,3315 |
2,80 |
0,4974 |
0,14 |
0,0557 |
0,44 |
0,1700 |
0,98 |
0,3365 |
2,90 |
0,4981 |
0,15 |
0,0596 |
0,45 |
0,1736 |
1,00 |
0,3413 |
3,00 |
0,49865 |
0,16 |
0,0636 |
0,46 |
0,1772 |
1,05 |
0,3531 |
3,20 |
0,49931 |
0,17 |
0,0675 |
0,47 |
0,1808 |
1,10 |
0,3643 |
3,40 |
0,49966 |
0,18 |
0,0714 |
0,48 |
0,1844 |
1,15 |
0,3749 |
3,60 |
0,499841 |
0,19 |
0,0753 |
0,49 |
0,1879 |
1,20 |
0,3849 |
3,80 |
0,499928 |
0,20 |
0,0793 |
0,50 |
0,1915 |
1,25 |
0,3944 |
4,00 |
0,499968 |
0,21 |
0,0832 |
0,52 |
0,1985 |
1,30 |
0,4032 |
4,50 |
0,499997 |
0,22 |
0,0871 |
0,54 |
0,2054 |
1,35 |
0,4115 |
5,00 |
0,499999 |
0,23 |
0,0910 |
0,56 |
0,2123 |
1,40 |
0,4192 |
|
|
0,24 |
0,0948 |
0,58 |
0,2190 |
1,45 |
0,4265 |
|
|
0,25 |
0,0987 |
0,60 |
0,2257 |
1,50 |
0,4332 |
|
|
0,26 |
0,1026 |
0,62 |
0,2324 |
1,55 |
0,4394 |
|
|
0,27 |
0,1064 |
0,64 |
0,2389 |
1,60 |
0,4452 |
|
|
0,28 |
0,1103 |
0,66 |
0,2454 |
1,65 |
0,4505 |
|
|
0,29 |
0,1141 |
0,68 |
0,2517 |
1,70 |
0,4554 |
|
|
0,30 |
0,1179 |
0,70 |
0,2580 |
1,75 |
0,4599 |
|
|
З врахуванням залежностей (6.1) і (6.2):
|
|
|
|
n |
mi |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
∑x i |
= ∑x i pi |
= x ср , |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
i=1 |
n |
i=1 |
|
|
|
|
|
|
|
|
|
|
|
||||
а також |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
mi |
= 1, |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
i=1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|||
залежність (5.24) набуде вигляду: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
n |
|
mi |
|
n |
|
mi |
|
n |
|
|
mi |
|
n |
|
mi |
|
|
|
|
||
D(x) = ∑xi |
2 |
|
− ∑2xi x cр |
|
+ ∑2x cр |
2 |
= |
∑x i |
2 |
− x |
|
2 |
(6.25) |
||||||||
|
n |
n |
|
|
|
ср |
|
||||||||||||||
i=1 |
|
i=1 |
|
i=1 |
|
|
n |
i=1 |
|
n |
|
|
|
||||||||
Враховуючи, те що: |
1) |
аналітичне |
вираження |
|
закону |
розподілу в |
загальному |
вигляді |
|||||||||||||
(y = f (x)) характеризує сукупність безперервних випадкових величин; 2) дискретна величина х від- повідає миттєвому значенню випадкової безперервної величини х; 3) відносна частота дискретної
10
