Комп. дискретна математика (методички) / Множини остаточний вар_ант

A B B A , що і потрібно було довести. ▲

Приклад 8.9. Знайти декартовий добуток множин A={1,2,3}, B={a,b} та його потужність.

Розв’язання:

A B = {(1,a), (1,b), (2,a), (2,b), (3,a), (3,b) }, B A = {(a,1), (a,2), (a,3), (b,1), (b,2), (b,3) }.

Як бачимо, A B B A.

Потужність декартового добутку: |A B|=|B A| = 3 2=6. ▲

Приклад 8.10. Довести рівність множин: (B) С=(A C)(B C)

Розв’язання:

Доведемо, що ( B) С(A C)(B C).

Нехай z(A B) С, тоді z=(x,y), де x A B та y С. Отже, x A або x В.

Тобто x A та y С або x В та y С. Тому z A C або z B C. За означенням об’єднання z(A C)(B C).

Доведемо, що ( B) С(A C)(B C).

Нехай z(A C)(B C), тоді z A C або z B C. Так як z=(x,y), то x A, y С або x B, y С.Отже, x A або x В при y С. Тому x A B і y С. За означенням декартового добутку z(B) С. ▲

Приклад 8.11. Зобразіть на координатній площині декартовий добуток множин А×В, якщо:

a)А= {1,2,3}, В=[3,5];

b)А={х ׀ x R, 1≤x≤3}; B={y ׀ y R, 3≤y≤5};

c)А=R, В=[3,5];

d)А=R, В=R.

Розв’язання:

а) Так як множина А складається з трьох елементів, а множина В містить всі дійсні числа від 3 до 5, включаючи і самі ці числа, то декартовий добуток А×В складатиметься з нескінченної кількості пар, перша компонента яких або 1, або 2, або 3, а друга – будь-яке дійсне число з проміжку [3, 5]. Безліч таких пар дійсних чисел на координатній площині зобразиться трьома відрізками (рис. 8.2).

21

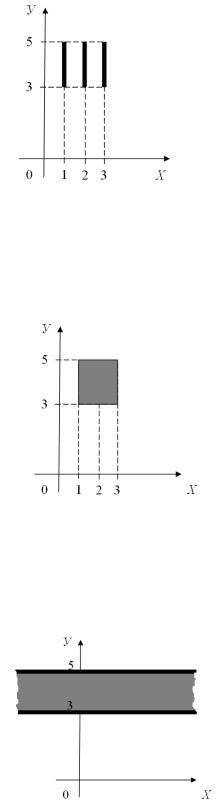
Рис. 8.2.

b) У цьому випадку нескінченними є обидві множини А і В. Тому першою координатою пари, що належить множині А×В, може бути будь-яке число з проміжку [1, 3], а другою – будь-яке число з проміжку [3,5] і, отже, точки, що зображують елементи декартового добутку даних множин А і В, утворюють квадрат (рис. 8.3).

Рис. 8.3.

с) Цей випадок відрізняється від попереднього тим, що множина А складається з усіх дійсних чисел, тобто абсциса точок, що зображають елементи множини А×В, приймає всі дійсні значення, в той час як ордината вибирається з проміжку [3, 5].

Безліч таких точок утворює нескінченну смугу (рис. 8.4).

Рис. 8.4.

d) Декартовий добуток R×R складається з різноманітних дійсних чисел. Точки, що зображують ці пари, суцільно заповнюють координатну площину.

Таким чином, декартовий добуток R×R містить стільки ж елементів, скільки точок знаходиться на координатній площині. ▲

22

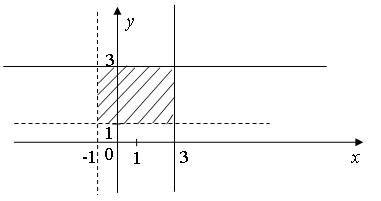
Приклад 8.12. На координатній площині побудувати множину (-1; 3×1; 3).

Розв’язання:

Першу множину поміщаємо на осі OX, другу на осі OY. Множина всіх пар, тобто декартовий добуток, зображається точками заштрихованого прямокутника, але без лівої та нижньої сторони (рис. 8.5).

Рис. 8.5 Декартовий добуток

Приклад 8.13. Скільки цілих чисел між 0 та 1000 містять рівно одну цифру 6?

Розв’язання:

Нехай S – множина цілих чисел між 0 та 1000, що містять рівно одну цифру 6. Розглянемо три підмножини S1, S2 та S3 множини S.

S1 – множина, яка містить число, що складається з однієї цифри і ця цифра 6;

S2 – множина, яка містить двохзначне число, що містить лише одну цифру, яка рівна 6;

S3 – множина, яка містить трьохзначне число, що містить лише одну цифру, яка рівна 6.

Множина S1 містить лише один елемент – число 6.Отже, S1=1.

У множині S2 кожен елемент, що містить 6, є або першою, або другою цифрою. Якщо 6 – друга цифра, то існує 8 різних чисел, які будуть стояти на першій позиції, оскільки перше число не може бути 0 або 6. Якщо 6 – перша цифра, то таких чисел 9, оскільки друга цифра не може бути рівна 6. Таким чином, S2 містить 8+9=17 елементів, тобто S2=17.

Елемент із S3 може містити 6 як першою, так і другою чи третьою цифрою. Якщо 6 – перша цифра, то існує 9 варіантів вибору другої цифри та 9 варіантів вибору третьої цифри. Згідно комбінаторному принципу множення, S3 містить 9 9=81 чисел з першою цифрою 6. Якщо 6 –друга цифра, то існує 9 варіантів вибору третьої цифри та 8 варіантів вибору першої цифри, оскільки перша цифра не може бути нулем. Очевидно, S3

23

містить 9 8=72 чисел, у яких 6 – друга цифра. Аналогічно, S3 містить 72 числа, у яких 6 – третя цифра. Отже, всього S3 містить 81+72+72=225 елементів, тобто S3=225.

Оскільки S S1 S2 S3 та множини S1, S2 і S3 – ті, що попарно не перетинаються, тоді

S S1 S2 S3 S1 S2 S3 1 17 225 243.▲

Приклад 8.14. Скільки додатних цілих чисел, менших 1001, діляться на

2, 3 чи 5?

Розв’язання:

Нехай X – множина додатних цілих чисел, які діляться на 2, 3 чи 5. Розглянемо три підмножини X1, X2 і X3 множини X.

X1 – множина додатних цілих чисел, які діляться на 2. Число елементів

X1 X 2 X 3 500 333 200 166 100 66 33 734.

Приклад 8.15. Про множини А, B, С відомо, що: A B C = {1, 2, 3, 4, 5,

24

6}, A B C = {3}, B A={1, 2, 4, 6}, B C ={2, 5, 6}, B / A / C = {2},A B / C {1, 2, 5}, A C / B {1, 6}.

Знайдіть множини А, B, С.

Розв’язання:

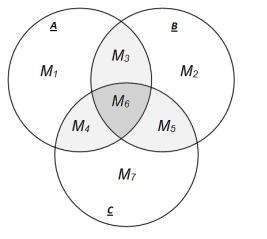
Зобразимо перетин трьох множин A, B, C на рис. 8.6. і позначимо всеможливі утворені множини Mi :

Рис. 8.6 Приклад перетину трьох множин

Складемо систему рівнянь:

1.A B C = M1 M2 M3 M4 M5 M6 M7 {1, 2, 3, 4, 5, 6};

2.A B C M6 ={3};

3.B A M1 M4 M5 M2 ={1, 2, 4, 6};

4.B C M2 M3 M4 M7 ={2, 5, 6};

5.B / A / C M2 = {2};

6.A B / C M1 M2 M3 ={1, 2, 5};

7.A C / B M1 M4 M7 ={1, 6}.

Отримаємо:

M 6 ={3}, M 2 ={2}.

Із рівнянь (6 - 7) зрозуміло, що M1 ={1}.

Тоді з рівняння (6) випливає, що M3 ={5}, а з рівняння (7) та (3) випливає, що M7 , а M 4 ={6}. Із рівняння (3) M5 ={4}.

Отже, A = M1 M3 M4 M6 {1, 3, 5, 6}, B = M2 M3 M5 M6 {2, 3, 4, 5}, C = M4 M5 M6 M7 {3, 4, 6}.

25

9.Завдання до виконання

1.Нехай А={{1,2,3}, {1,3}, 1, 2}. Чи справедливо, що

a){1, 2}А;

b){1, 2} A.

2. Перелічити елементи множини:

3. Перелічити елементи наступних множин:

a)A {x | x {{a,b},{a,b,c},{a,c, d}}};

b)B {x | x {a,b,c, d}};

c)C {x | x {a,b, c, d}}.

4. Нехай А – довільна множина. Що являють собою наступні множини:

a)A ;

b)A \ ;

c)A \ A;

d)A .

5. Записати множини, перелічивши їх елементи. Яка потужність даних множин?

a)А = {n | n — додатні числа, кратні 7 і менші 60};

b)В = {x ׀x2 - 5x + 6 = 0}.

6. Записати усі підмножини множини А ={а, b, с}.

a)Чи рівні множини {a, b, c, d} і {b, d, с, а}?

b)Нехай М = {чотирикутники}. Чи належать до множини М такі фігури: квадрат, ромб, коло, шестикутник?

7. Нехай А – множина цілих чисел, що діляться на 4, а В – множина цілих чисел, що діляться на 3. Які з чисел 9, 0, -24, -53, 128, 242048 входять у множину A B ?

8. Нехай А = {1, 2, 3, 4, 5, 6, 7} і В = {2, 4, 6}. Знайти:

a)суму С;

b)різницю R;

c)переріз Р множин А і В.

9. Нехай Ν = {натуральні числа}, М ={додатні раціональні числа}, Р={прості

числа}, Q = {додатні непарні числа}. Чи правильне твердження

P M (Q N) M ?

26

10. Нехай А – множина, що складається з 30 стільців, а В – множина, що складається з 30 студентів. Чи А=В ? Обґрунтувати відповідь.

11. За допомогою наочного зображення на площині впевнитись, що для будьяких трьох множин А, В і С справджуються такі рівності:

a)A (B C) (A B) (A C) ;

b)A (B C) (A B) (A C) .

12. Користуючись кругами Ейлера, довести рівності:

a)A \ B A \ (A B) ;

b)A (A B) \ (B \ A) .

13. Вказати, які з поданих нижче множин скінченні, а які нескінченні (поясніть, чому):

a)множина цілих чисел, що діляться на 5;

b)множина коренів заданого многочлена;

c)множина всіх рослин на Землі.

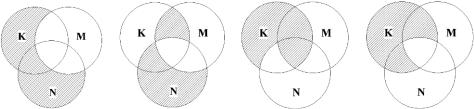
14. Записати формули, відповідні до діаграм Венна:

15. Зобразити на координатній площині декартові добутки множин А та В. У задачі b записати також усі елементи декартових добутків:

a)A { x | x R,3 x 5 };B { x | x R,3 x 6 } ;

b)A { x | x Z ,3 x 5 };B{ x | x Z ,3 x 6 } .

16. Задані множини A={a,b,c}, B={x,y}, C={0,1}. Побудувати декартові добутки а-d:

a)A B C ;

b)C B A ;

c)C A B ;

d)B B B .

17. Задані множини А={a,b,c,d,e} та В={a,b,c,d,e,f,g,h}. Побудувати множини а-d:

a)A B;

27

b)A B ;

c)А\В;

d)В\А.

18.Знайти множини А та В, якщо А\В={1,5,7,8}, B\A={2,10} та

B A={3,6,9}.

19.А та В – множини. Довести рівність A\B=A B .

20.А та В – множини . Довести рівність A B A B) A .

21. Нехай А, В та С – довільні множини. Довести, що:

a)A (B C) (A B) C;

b)A (B C) (A B) C.

22.Задані множини А, В та С. Довести рівність множин

(A \ B) \ C (A \ C) \ (B \ C).

23.Задані множини А={0,2,4,6,8,10}, B={0,1,2,3,4,5,6} та С={4,5,6,7,8,9,10}.

Побудувати множини:

a)A B C ;

b)A B C ;

c)( A B) C ;

d)( A B) C.

24. Чи можна стверджувати, що А=В, якщо А, В та С – множини, для яких виконані такі рівності:

a)A C B C ;

b)A C B C ;

c)A C B C .

25. Нехай А, В та С – довільні множини. Довести, що:

| A B C | | A | | B | | C | | A B | | A C | | B C | | A B C | .

26. Множина А складається із натуральних чисел, що діляться на 4, множина В – із натуральних чисел, що діляться на 10, множина С – із натуральних чисел, що діляться на 75. Із яких чисел складається множина A B C ?

27. Дано довільні множини А, В, С такі, що: A B і A C; A C і B C. Чому рівні вирази:

a)A B C;

28

b)A B C.

28. Задано довільні множини А, В, С такі, що A B, B C . Чому рівні множини:

a)A B C;

b)A B C;

c)A \ C;

d)C \ A.

29. Задані множини:

a)А={h,o,t} і B={t,o,o,t,h};

b)A={r,e,s,t} і В={s,t,r,e,e,t}.

Чи правильно, що A B? B A? A B?

30. Відомо, що:

a)A B C A;

b)A B C A.

Що випливає з даних рівнянь?

31. Задано, що S={a1, a2, a3}, причому відомо, що A S , A={a1, a2}; B S , B={a2, a3}; C S ; C={a2}. Знайти елементи наступних множин:

a)A A;

b)A B;

c)B A;

d)(A B) (B C).

32. Нехай U={1,2,3,4,5}, X={1,5}, Y={1,2,4}, Z={2,5}.

Знайти множини:

a)X Y ;

b)( X Z ) Y ;

c)X (Y Z ) ;

d)(X Y ) (X Z);

e)X Y;

f)X Y ;

g)X Y;

h)( X Y ) Z;

i)X (Y Z );

j)X \ Z;

k)(X \ Z ) (Y \ Z ).

29

33. Нехай U ={a,b,c,d,e,f}, A={a,b,c}, B={f,e,c,a}, C={d,e,f}.

Знайти множини:

a)A \ C;

b)B \ C;

c)C \ B;

d)A \ B;

e)A B;

f)B A;

g)A C;

h)C A;

i)C A.

34. Задані дві довільні множини А та В такі, що A B . Як виглядають множини A \ B та B \ A?

35. Задані дві довільні множини С та D такі, що C D . Як виглядають множини C D та C D?

36. Задано довільну множину Х. Знайти множини:

a)X X ;

b)X X ;

c)X \ X ;

d)X \ X .

37. Які з наступних тверджень правильні:

a)0 ;

b){0};

c)|{ }|1.

38. Спростити вирази:

a)A B B;

b)( A B) ( A B ) ( A B);

c)( A B ) ( A B) ( A B);

d)( A \ B \ B C) \ C D;

e)(A A B A C) A B \ C;

f)A B B C \ B;

g)(A A B A C) A B C ;

30