
n1
.pdf
61
Условие (1.63) выполняется при длительностях импульса b2 a . Для
a . Для
b ~ 10-5 см, a ~ 1 см2/с, b2  a ~ 10-10 с.
a ~ 10-10 с.
То есть (1.63) хорошо выполняется при временах воздействия 10-10 с за счет выравнивания температуры теплопроводностью или же за счет непосредственного тепловыделения при поглощении (при толщинах ~ 100 A для металлических пленок).
Будем считать также, что подложка прозрачная, то есть все излучение поглощается в пленке
f2 0
Одно из сильных и правильных допущений уже сделано: за время импульса пленка прогрелась равномерно и поэтому T1 (x,t) T1 (t) , что справедливо
при b2 a1t или t 4b2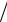 a1 .
a1 .
Это позволяет интегрировать (1.60) по всей толщине пленки:
|
b |
T1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
q0 A1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
a1 |
|
|
|
|
T1 |
dx |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
bc1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
0 |
t |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
1 |
|
b a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
t |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Используя граничные условия (1.61, 1.62) получим новое граничное усло- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вие |
|
|
T1 |
|
|
|
|
|
|
|
|
|
|
|
|
dT2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
c b |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
q |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
1 |
|
|
|
t |
|
|
|
|
|
|
|
|
2 |
|
|
|
dx |
|
|
x b |
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
k |
|
|
|
T2 |
|
|
|
|
|
|
|
|
q |
|
|
A c b |
T2 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
2 x |
|
|
x b |
|
|
|
|
|
|
|
|
|
|
0 1 |
|
|
|
|
1 |
|
|
|
t |
|
x b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Решение для T1 (t) будет: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c22a2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
q A b |
|
|
2 |
|
|
|
|
|
a2t c |
|
|
c |
|
at |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
T1 (t) |
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
e |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
(1.64) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
c2 |
|
|
|
c2b |
|
|
1 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Видно, что характерными параметрами в (1.64) являются: b, lT ~ |
|
|
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a2t |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рассмотрим частные случаи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
2 b2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
1) Малые времена воздействия: c b c |
|
|
|
|
|
|
t t |
|
c |
|
a2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
a |
t |
0 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|||
Возьмем |
|
для |
|
|
|
|
примера металлическую |
|
пленку на |
стекле: b ~ 10-5 см, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a2 6∙10-3 см2/с, |
|
|
t0 |
~ 10 8 |
|
с – пленка греется фактически в условиях тепловой |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
изоляции. В этом случае все определяется пленкой: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
T (t) |
q0 A1t |
|
Q0 (t)A1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
c1b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c1b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2) Большие времена воздействия t t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
q0 A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
T (t) |
|
a2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||

62
Времена большие, потери тепла на нагрев пленки ничтожны. Пленка греется так же как полупространство из материала подложки, но с оптическими свойствами пленки.
В полной постановке задача о нагреве источником тепла постоянной интенсивности q0 двухслойного материала при идеальном тепловом контакте
между слоями формулируется следующим образом:
T1 |
|
a |
2T1 |
; |
|
|
|||
|
|
|
|
|
|||||
t |
1 z2 |
|
|||||||
t 0, |
|
|
|
|
|
|
|||
b z 0; |
|||||||||
T2 |
|
|
|
2T2 |
|
|
|||
a |
; |
|
|||||||
|
|
||||||||
t |
2 z2 |
|
|
||||||
t 0, |
|
|
|
|
|
|
|||
z b. |
|||||||||
Краевые условия задачи имеют вид
z 0, S1 T1 A1q0 ,
z
|
|
T T , |
|
|
||
z b |
|
1 |
2 |
|
T |
, |
|
|
T |
||||
|
|
S1 |
1 |
S 2 |
2 |
|
|
|
z |
||||
|
|
|
z |
|
||
t 0, |
T1 T2 0. |
|
|
|||
(1.65)
(1.66)
(1.67)
(1.68)
Соотношения (1.67) описывают идеальный тепловой контакт между слоями (равенство температур и тепловых потоков на границе). Предполагается, что амплитуда плотности мощности излучения постоянна во времени:
(t) 1 при t 0.
Решение задачи (1.65) (1.68) имеет вид
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2A1q0 |
|
|
|
|
|
|
|
|
z |
|
|
|
n |
|
|
|
2nb z |
|
|
|
|
|
2nb z |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( g) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
T1(z,t) |
|
|
|
|
|
|
|
a1t i |
|
|
|
|
i |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
; |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 a1t |
|
|
|
|
|
2 a1t |
|
|
|
2 a1t |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
S1 |
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2n 1)h (z h) |
|
1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
2A1q0 (1 g) |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
||||||||||||||||||
T2 (z,t) |
|
|
|
|
|
|
|
|
|
|
|
|
a1t |
( g) i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 a1t |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
S1 |
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
S1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
S 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где g |
|
|
a1 |
a2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
S1 |
|
|
|
|
S 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
a1 |
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
63
1.3.7. Нагрев материалов в интерференционном лазерном по-
ле.
Представляет интерес рассмотреть нагревание поверхности полупространства, освещаемой излучением, распределение которого определяется интерференционным полем (рис. 1.23). Это распределение можно описать выражением вида:
q0 ( y) |
q |
0 1 cos(gy) |
g 2 d |
Рис. 1.23. Распределение интенсивности при интерференции.
Температурное поле на поверхности можно представить в виде двух слагаемых:
Tc (y,t) T1(t) T2 (y,t)
Первое из них описывает температуру поверхности, которую определяет усредненное по y лазерное излучение.
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
2 |
q |
|
A at |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
T (x,t) |
T i |
|
|
|
|
|
, |
T (t) |
|
|
0 |
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
1 |
10 |
|
|
at |
|
10 |
|
k |
||||||||||||||
Второе – вклад пространственно промодулированной составляющей. При оценке вклада в нагревание пространственно промодулированной составляющей излучения мы имеем дело в рассматриваемом случае с так называемым тепловым диполем. Усредняя модуляционный член по y , очевидно, получим 0. Дополнительного нагрева за счет модуляционного члена принципиально не получить, есть лишь дополнительный по отношению к среднему значению плотности мощности излучения приток тепла, но есть и его точно такой же отток, что в среднем дает ноль. Этот член может привести только к модуляции среднего значения температуры. Решение задачи имеет вид:
T2 ( y, x,t) q0 g
 at cos(gy)e gx , kg
at cos(gy)e gx , kg
Как и следовало ожидать, распределение температуры на поверхности пропорционально cos(gy)
T2 ( y) ~ cos(gy).
Рассмотрим, как изменится распределение температуры при больших временах воздействия:
64
t |
1 |
|
~ |
d 2 |
, x ~ d |
|
|
|
|||
|
ag |
2 |
|
a |
i? |
|
|
|
Температура поверхности будет стремиться к
T20 q0 cos(gy) , kg
то есть даже в условиях, когда времена большие, теплопроводность не сглаживает модуляцию полностью, перепад температур остается:
T |
|
2q |
0 |
. |
(1.69) |
|
|
||||
20 |
|
kg |
|
||
|
|
|
|||
Выражение (1.69) определяет тепловую разрешающую способность лазерного излучения с интерференционным распределением.
В условиях, когда в системе есть положительные обратные связи, даже малые T20 могут играть важную роль.
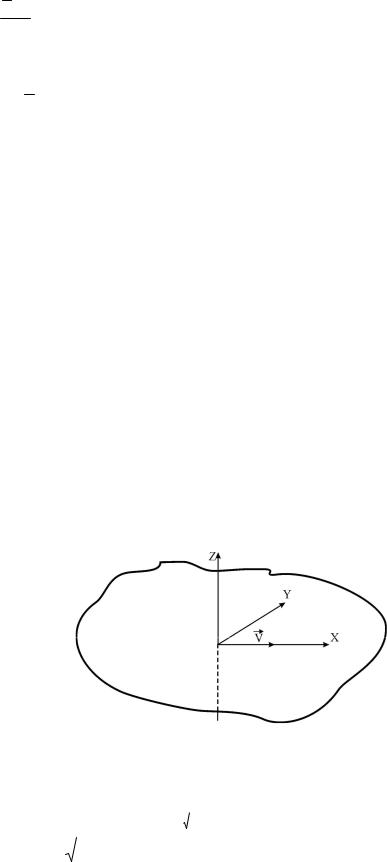
1.3.8. Особенности нагрева материала движущимся световым пятном.
Во многих практических применений лазерная обработка происходит движущимся по поверхности материала пятном лазерного излучения. Если пятно движется по поверхности, то независимо от характера теплоотвода и теплообмена происходит стабилизация температуры, связанная с тем, что при движении источника в процесс нагрева вовлекаются все новые и новые участки поверхности.
Рассмотрим случай, когда тело массивное, то есть его можно представить в виде полупространства, а источник точечный: его размеры малы по сравнению с длиной теплопроводности. Источник движется по поверхности со скоростью V в направлении x (см. рис. 1.24). Мощность источника p qS (S – его площадь).
Рис. 1.24. Схема движения точечного источника по поверхности тела.
В этом случае распределение температуры по поверхности (z=0) в движущейся системе координат имеет вид:
|
|
p |
|
|
V |
|
|
|
|
|
|
|
|
|
2 |
|
2 |
||||
|
|
|
|
|
x |
x |
y |
|
|
|
|
|
|
|
|
||||||
T (x, y) |
|
|
e 2a |
|
|
|
|
|||
|
|
|
|
|
|
|
||||
0 |
2 k |
x2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

|
|
|
|
|
65 |
|||
На оси ( y 0) выражение становится совершенно простым: |
||||||||
|
|
p |
|
|
|
Vx |
|
|
|
|
e |
a x 0 |
|||||
T (x,0) |
|
|
|
|
||||
|
|
|||||||
2 kx |
1.70 |
|||||||
0 |
|
|
p |
|
|
|
|
|
|
|
|
|
|
x 0 |
|||
|
|
|
|
|
||||
|
|
|
2 kx |
|||||
Из выражения (1.70) видна особенность нагревания движущимся источником: материал впереди него (x 0) прогревается слабо. Характерная область прогрева впереди: lT a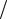 V . Позади себя движущийся источник оставляет слабо затухающий температурный шлейф (см. рис. 1.25).
V . Позади себя движущийся источник оставляет слабо затухающий температурный шлейф (см. рис. 1.25).
Рис. 1.25. Распределение температуры от движущегося источника в движущейся системе координат.
Результат воздействия зависит от соотношения двух времен: эффективного времени воздействия - времени прохождения пятном излучения своего диаметра tu d0 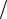 V , (d0 2r0 ) и теплопроводностного времени tT r02
V , (d0 2r0 ) и теплопроводностного времени tT r02 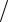 a ,
a ,
Рассмотрим частные случаи.
1. Быстродвижущийся источник.
V 2a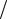 r0 , tu tT (тепло не успевает выйти из зоны облучения). Воздействие аналогично разогреву полупространства импульсом с дли-
r0 , tu tT (тепло не успевает выйти из зоны облучения). Воздействие аналогично разогреву полупространства импульсом с дли-
тельностью tu d0  V .
V .
T |
2qS atu |
|
2 2qS |
ar0 |
|||||
|
|
|
|
|
|
|
|
||
m |
k |
|
k |
V |
|||||
|
|
||||||||
2) Медленнодвижущийся источник.
При t tu происходит стабилизация температуры за счет теплопроводности, поэтому источник можно считать неподвижным:
T (0) qS r0 .
S
66
1.4. Нелинейные режимы лазерного нагрева.
1.4.1. Нагрев с учетом температурной зависимости поглощательной способности.
Практически все задачи, связанные с воздействием мощного лазерного излучения на металлы, являются нелинейными в том смысле, что и теплофизические (c , a , s ) и оптические постоянные ( A, R , n ) металлов зависят от температуры и, следовательно, от интенсивности лазерных источников.
Рассмотрим общий подход к решению нелинейных задач теплопроводности на примере влияния температурной зависимости оптических постоянных металла на характер его нагрева лазерным излучением.
При учете аномального скин-эффекта поглощательная способность металла A может быть представлена в виде
A A0 bT , |
|
(1.71) |
где A - поглощательная способность металла, |
определяемая рассеиванием |
|
электронов проводимости на примесях, дефектах, |
b p |
2 0 - параметр, оп- |
ределяемый статической электропроводностью металла 0 и плазменной час-
тотой p . Обычно величина b (1 5) 10 5 К 1 . При быстром лазерном нагреве
металла до температур T |
~ 1000 К произведение bT ~ (1 5)·10 2 . Для боль- |
шинства металлов A ~10 2 |
, то есть температурную добавку bT в поглощатель- |
0 |
|
ную способность металла надо учитывать (см. таблицу 1.3). |
|
Рассмотрим как в условиях линейной положительной обратной связи будет вести себя разогрев металла. Постановка краевой задачи нагрева полубесконечного пространства в одномерном случае при отсутствии объемных источников имеет следующий вид
|
T |
|
a |
|
2T |
|
|
|||
|
t |
|
|
z2 |
|
|
||||
|
|
|
|
|
|
|
||||
|
s |
|
T |
|
z 0 |
q (A bT ) |
(1.72) |
|||
|
|
|||||||||
|
|
|
|
|
||||||
|
|
|
z |
|
0 0 |
|
||||
|
|
|
|
|
||||||
T (z,0) T ( ,t) T0 , Ab (A0 |
bT0 ) |
|||||||||
T0 - начальная температура. |
|
|||||||||
Таблица 1.3. Параметры, определяющие температурную зависимость поглощательной способности для ряда металлов
Материал |
A0 |
b 10 4 |
K 1 |
A при 700 К |
Волфрам |
0.24 |
1.03 |
|
0.31 |
Молибден |
0.0 |
0.99 |
|
0.07 |
Тантал |
0.048 |
0.92 |
|
0.049 |
Платина |
0.099 |
0.64 |
|
0.10 |
Медь |
0.028 |
0.14 |
|
0.037 |
Графит |
0.890 |
-0.40 |
|
0.76 |
67
Германий |
0.747 |
-0.92 |
0.69 |
Задача (1.72) позволяет найти аналитическое выражение для температуры поверхности металла и ее изменения во времени. Решение может быть получено операционным методом в виде
T (t) T0 |
|
Ab |
exp( t) *( |
|
|
) 1, |
|||||||
t |
|||||||||||||
|
|||||||||||||
|
|
|
|
b |
|
|
|
|
|
|
|
||
где 1 t |
|
q2b2a |
2 |
, |
*( |
|
|
) - интеграл ошибок. При этом |
|||||
0 |
|
t |
|||||||||||
|
|
0 |
|
s |
|
|
|
|
|
|
|||
A(t) Ab exp( t) *( 
 t )
t )
Для удобства анализа введем параметр y0 q0b
 at
at  s , который, имея размерность длины, характеризует тот прогретый слой металла, который осуществляет положительную обратную связь в системе лазерное излучение - металл и изменение условий поглощения лазерного излучения, что эквивалентно изменению мощности теплового источника на поверхности.
s , который, имея размерность длины, характеризует тот прогретый слой металла, который осуществляет положительную обратную связь в системе лазерное излучение - металл и изменение условий поглощения лазерного излучения, что эквивалентно изменению мощности теплового источника на поверхности.
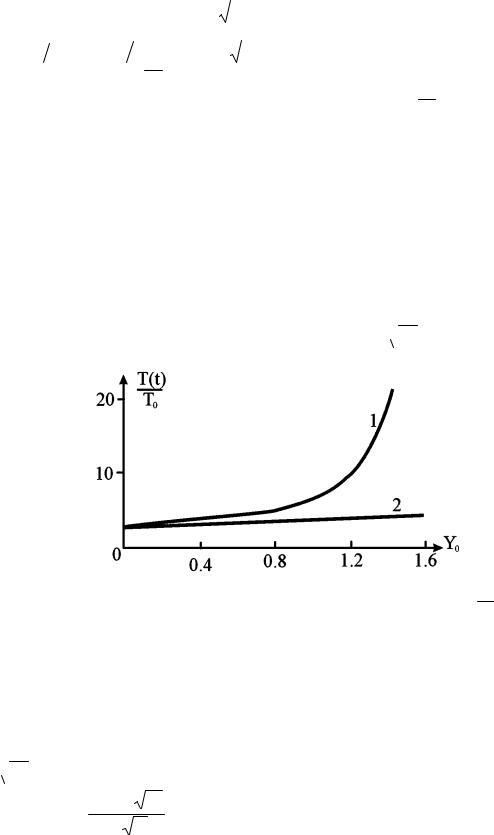
Изменение температуры поверхности металла во времени для случаев A const и A(T ) представлено на рис. 1.26
Очевидно, что температурная зависимость поглощательной способности металла приведет к особенностям нагрева тела. При этом в зависимости от времени, определяющего вклад в изменение процессов поглощения лазерного излучения, вносят либо множитель exp( t), либо * ( 
 t ).
t ).
Рис. 1.26. Отношение текущей температуры поверхности металла T0 (t) к
начальной температуре T0 в зависимости от параметра y0 q0b
 at
at  s с учетом
s с учетом
температурной зависимости поглощательной способности - 1; при неизменной
поглощательной способности метала – 2
При t t0 , когда y0 1 превышение T над T0 невелико, малы и изменения поглощательной способности A. Металл ведет себя как материал с постоянной поглощательной способностью A(T ) Ab и тогда, поскольку
( 
 t ) 2 , а exp( t) 1
t ) 2 , а exp( t) 1
T (t) T 2q0 Ab at . |
||
0 |
s |
|
|
||

68
При более длительном воздействии лазерного излучения на металл параметр y0 1 и
T T0 2Ab exp( t) . b
Происходит стабилизация прогретого слоя металла по толщине, причем
l |
|
T0 |
|
|
T0 S |
|
S |
, |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
T |
T |
|
|
q (A bT ) |
|
q b |
|
|
|
|
|||||
|
|
|
|
|
|
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
x |
x 0 |
|
|
|
|
|
|
|
|
|
|
||
При bT A |
получаем |
l |
|
S |
q b |
и a e2 , а t |
l2 |
a - характерное |
|||||||
|
|
|
|
|
b |
|
|
T |
|
0 |
T |
T |
|
||
время выхода процесса на режим предельного разогрева (рис. 1.27).
Рис. 1.27. Выход режима лазерного нагрева металла на предельный режим
Очевидно, что lT определяет толщину прогретого слоя металла, которая практически не зависит от времени воздействия лазерного пучка, но определяется величиной мощности теплового источника на поверхности материала. Тогда безразмерный параметр y0 , введенный ранее, есть не что иное, как, отношение толщины металла, нагретого за счет процессов теплопроводности, к lT .
Можно легко определить время, которое определяет точку перегиба
функции T (t) , обычно оно определяется как |
t 0.2t |
, при истечении этого |
|||
|
|
|
|
|
T |
времени температуру поверхности металла можно определить как |
|||||
T * (t) T (t) T 0,81 |
A |
|
|
|
|
|
|
|
|
||
0 |
b |
|
|
|
|
|
q0 |
3*1010 |
Вт/м2; b 2 10 5 К 1 ; a |
||
В частности для меди s 40 Вт/мК; |
|||||
= 1.2 10-4 м2 с 1 ; t 0,2 2 |
q2b2a 0,2 10 2 |
с, |
т.е. выход лазерного нагрева ме- |
||
S |
0 |
|
|
|
|
ди на предельный режим вполне реален даже в случае облучения металла импульсами твердотельных лазеров, при работе последних в режиме свободной генерации. При этом температура поверхности достигает величины Т* (t)~700° K.
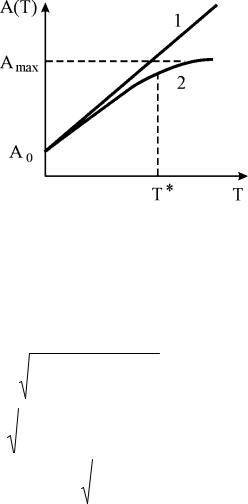
Следует отметить, что реально величина поглощательной способности металлов не может быть больше, чем Amax 1. По этой причине функциональную зависимость A(Т) можно более реально описать не соотношением типа (1.71), а зависимостью
|
|
|
69 |
|
|
T T |
|
|
(1.73). |
||
A(T ) A0 bT; |
|||
|
Amax ; |
T T |
|
где T - некоторая характерная для заданного материала температура. Зависимости T (t) и A(T ) в случае линейной (модельной) зависимости и с
учетом зависимости (1.73) (реальный случай) представлены на рис. 1.28.
Рис. 1.28. Зависимость A(T) без учета конечности поглощательной способности (1) и с учетом (2)
Можно аналитически решить и задачу о нагревании металла с учетом зависимости поглощательной способности материала от температуры T . При наличии отрыва температуры электронного газа Te и от температуры решетки Ti имеем окончательно
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
a |
0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Ai |
|
1 1 4 f0 4 f |
|
|
|
|
|
|
|
|
|
|
|||||||||
T |
(t) T (t) |
|
|
|
|
|
|
|
|
|
|
|
|
e t |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
i0 |
|
|
0 |
|
|
b |
|
|
|
|
|
2 a 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
1 4 f0 |
4 f0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
a |
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 4 f0 4 f |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
2 |
|
|||||||||||||||
|
|
q0 |
|
|
|
|
|
|
a 1 2 f0 |
|
|
|
|
||||||||||||||
где: f0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||||||
|
k |
lпр |
|
|
2 2 a 0 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
0 c / – время начала разогрева кристаллической решетки металла, 1 - толщина скин-слоя.
- толщина скин-слоя.
Учет температурной зависимости поглощательной способности металла от температуры приводит к заметному отличию в плотностях лазерных потоков, необходимых для достижения максимальной температуры поверхности к концу действия импульса. Например, для серебра учет поправки снижает необходимые мощности потока на 30% (с q 3 1010 Вт/м2 до q *= 9·109 Вт/м2).
Очевидно, что рост температуры поверхности не прекращается при достижении температуры плавления металла. При этом максимальная температура нагревания связана с началом интенсивного процесса испарения материала с поверхности, ибо в металлах поглощение лазерного излучения практически всегда происходит на поверхности. Верхняя температурная граница нагрева материала зависит от многих факторов: длительности лазерного импульса, подво-
70
димой мощности, условий фокусировки лазерного пучка, окружающей атмосферы, обычно
Tn T* Te
Оценки T * можно провести следующим образом. Рассмотрим предельный случай мгновенного нагрева поверхностного слоя материала. В этом случае T * можно определить из соотношения
(1 R)q0 T * SlT c, (1.74)
где S - площадь облучаемой поверхности, - плотность, c - удельная теплоемкость металла, T* T - изменение температуры расплава, R - коэффициент отражения, lT ~ 1 Положим q0 1 Дж (АИГ:Nd 3 ) (умеренные лазерные пото-
ки), R=0.9, 1 10 7 м, S 10 4 м2, 104 кг/м3, c 103 Дж/кгК. Постановка
этих числовых значений в (1.74) даст значение T* 103 К, что совпадает с ранее сделанными оценками
Рассмотрим влияние температурной зависимости поглощательной способности при облучении области размером r0 .
При постоянной поглощательной способности ( A A0 ) температура в центре области облучения на поверхности будет
T0 q0 Ar0 ,
S
если же A A0 bT0 , то
|
|
q0 A0r0 |
|
|
|
|
|
T0 |
|
S |
|
. |
(1.75) |
||
1 |
q0br0 |
|
|||||
|
|
|
|
||||
|
|
|
|
|
|||
S
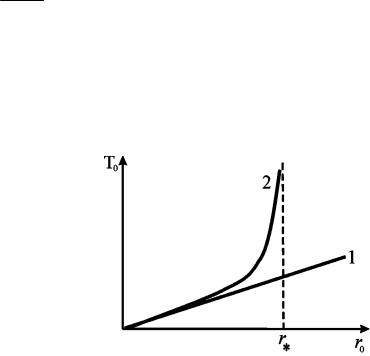
Рис. 1.29. Зависимость температуры от r |
при учете зависимости A(T ) |
||
Как следует из (1.75), возникает неустойчивость при r r , |
|||
r |
S |
, |
(1.76) |
|
|||
|
q0b |
|
|
|
|
||
