n1

31

ным временем диффузии через скин-слой) или N02 D T 2 (временем насыщения диффузантом поверхности металла до предела растворимости N0 f T ). Здесь D T D0 exp Td T — коэффициент диффузии с энергией активации Td (в Кельвинах); — поток атомов кислорода через границу металла из газовой фазы или из окисла.

Оценки показывают, что даже при N0 1020 1022 см–3 величина td определяется диффузией кислорода в металле независимо от того, как изменяется температура. В общем виде td находится из условия:

td

2 D T t dt .

0

Например, для титана ( 10 5 см для 10.6 мкм), как следует из оценок по этой формуле с использованием данных из табл. 1.1, время насыщения скин–слоя кислородом составляет: при T 7500 С td 3.5 с, а при T 12000 С td 1 мс. Толщина образующихся за эти времена при соответствующих температурах окисных пленок при изотермическом окислении составляет

и

bl bT Td Ta

при лазерном.

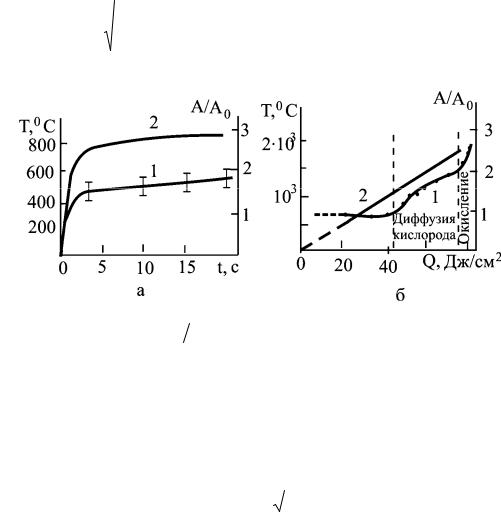
При указанных выше значениях td величина bT не превышает 2 10–5 см, поэтому окисные пленки не влияют на ИК–поглощение титана. В то же время, при лазерном разогреве до указанных температур в течение времени td термически тонких титановых фольг наблюдается почти двукратное возрастание поглощательной способности титана на 10.6 мкм по отношению к исходному значению (рис. 1.8).

Таблица 1.1. Параметры взаимодействия титана с кислородом

Кинетику изменения поглощательной способности металла в процессе диффузии и растворения кислорода аналитически можно описать в том случае, когда происходит лишь изменение частоты электронных столкновений и во всей области изменения поглощательной способности реализуются условия высокочастотного нормального скин эффекта: p . Тогда можно найти

добавку Ap к поглощательной способности металла A0 , связанную с дополни-

тельным примесным рассеянием электронов

где p z,t ep F n z,t определяется мгновенным распределением по глуби-

не металла ( z ) диффундирующих атомов кислорода n z,t . Здесь ep — сече-

которое при условии, что сначала (t 0) поверхность металла (z 0 ) насыщается кислородом вплоть до предела растворимости N0 , а перепад температур в пределах диффузионного слоя несуществен, имеет вид:

Рис. 1.8. Зависимости необратимого изменения относительной

33

t

2 D T t dt

Характерное время нарастания поглощательной способности по порядку величины согласуется с приведенной выше качественной оценкой, соответствующей значению 2 в точном выражении (1.27). Кроме того, одно и то же значение A достигается при тем меньшей температуре лазерного нагрева, чем меньше его скорость. Такая особенность объясняется одновременным ростом эквивалентного времени диффузии.

Еще один специфический механизм, приводящий к изменению поглощательной способности в результате термохимических процессов в скин–слое, можно наблюдать при лазерном нагревании сплавов. Он заключается в том, что вследствие преимущественного окисления некоторых компонентов сплава при его нагреве импульсным лазерным излучением на воздухе изменяется их процентное содержание в скин–слое. Качественные особенности механизма удобно пояснить на примере бинарного окисляющегося сплава М1М2 с резкой границей между ним и образующимся окислом. Зависимость поглощательной способности такой системы от содержания компонентов, аналогично зависимости электросопротивления, немонотонна – существует максимум (рис. 1.9).

Поэтому по мере роста окисной пленки и обеднения приповерхностного слоя сплава одним из элементов (для определенности примем, что таким элементом является М2, см. рис. 1.9) величина A будет возрастать или убывать в зависимости от того, по какую сторону от экстремума ( Amax ) находятся начальное (An ) и конечное ( Ak ) состояния системы. Очевидно, что в данном случае, как и при диффузии кислорода в металл, оптические свойства сплава изменятся, когда толщина обедненного слоя станет близкой к ~ 10 5 см.

Этому соответствует образование окисных пленок толщиной b ~ , которые слабо влияют на ИК–поглощение металлов. Поэтому на начальном участке лазерного окисления изменение поглощательной способности сплава полностью определяется процессами в его скин–слое. Наиболее интересным здесь является случай уменьшения величины A (на рис. 1.9 обозначен цифрой 1), который по внешним проявлениям сходен с эффектом лазерной очистки поверхности образца от примесей и загрязнений, но на самом деле может иметь иную, чисто термохимическую природу.

Более строгий подход к определению поглощательной способности облученного сплава требует решения волнового уравнения для пространственно неоднородной среды, проводимость которой ( ) меняется с расстоянием от границы отражения (z ) за счет изменения относительного содержания ( ) одного из элементов (например, хрома в нержавеющей стали) по линейному законуzz0 , где z0 — характерный размер области, обедненной этим элементом,

при 0.1 0 .

При 4z1 1 справедливо выражение:

34

мальном скин–эффекте.

Рис. 1.9. Поглощательная способность бинарного сплава в зависимости от процентного содержания элементов М1 и М2. Пунктиром показаны изменения A

между начальным ( An ) и конечным ( Ak ) значениями: 1 — с уменьшением A; 2 — с

возрастанием A.

1.2.6. Лазерное плавление поверхности

Плавление при лазерном воздействии рассматривают на основе взглядов на плавление при изотермическом нагревании. Характерная зависимость температуры от времени при плавлении приведена на рис. 1.10. Следует отметить постоянство температуры тела при непрерывном подводе тепла в процессе перехода кристалл – расплав, характерное для всех кристаллов. Процесс плавления происходит только в кристаллических веществах. При нагревании аморфных тел характерной температуры плавления нет, плотность, вязкость и другие свойства изменяются непрерывно, а не скачком как при плавлении.

При температуре плавления Tm происходит фазовый переход с поглощением скрытой теплоты перехода Lm . Учет теплоты фазового перехода приводит к необходимости решения нелинейной краевой задачи теплопроводности, которая называется задачей Стефана.

В случае чистых металлов условие Стефана, которое учитывает наличие скрытой теплоты фазового перехода, можно записать в виде

35

где n — нормаль в каждой точке к поверхности раздела фаз твердое тело – расплав; z(t) — координата границы раздела фаз в произвольный момент времени, отсчитываемого от момента достижения на поверхности температуры плавления. Целью решения задачи Стефана является отыскание соотношений для нахождения температурного поля T (x, y, z,t) в твёрдой и жидкой фазах металла и скорости перемещения границы раздела фаз при продолжении действия на него лазерного излучения.

Рис. 1.10. Остановка изменения температуры при плавлении кристаллического тела. По оси абсцисс отложено время, пропорциональное

равномерно подводимому к телу количеству теплоты.

В общем случае постановка краевой задачи теплопроводности с учетом плавления сложна, но некоторые реальные допущения позволяют получить ее аналитическое решение. Эти допущения следующие: 1) теплофизические свойства фаз не зависят от температуры; 2) в жидкой фазе происходит выравнивание температуры фазы до температуры плавления; 3) время плавления таково, что можно не учитывать теплообмен гетерофазной структуры твердое тело – расплав с окружающей средой. В этом случае получается однофазная задача Стефана относительно температуры в металле с нелинейными граничными ус-

T[h(t),t] Tm

T (l,t) T (z,0) T0 ,

где T T (z,t) – температурное поле, образующееся в металле под действием теплового источника на поверхности; q0 – плотность мощности лазерного им-

36

пульса; h(t) – положение границы фазового перехода, т.е. глубина проплавления материала; Lm - скрытая удельная теплота плавления; T0 (z) - начальная температура; l - толщина металла.

Второе уравнение системы (1.29) выражает закон сохранения энергии при плавлении. Оно выполняется как в процессе перемещения фазовой границы dhdt 0 (T (h,t) Tm ), так и при нагреве поверхности (T (0,t) Tm , dhdt 0 ). В случае воздействия на поверхность металла импульсного лазерного излучения время от начала действия импульса лазера до достижения на поверхности температуры плавления, очевидно, зависит от теплофизических свойств материала, формы лазерного импульса и мощности теплового потока. В случае q0 const можно получить

Решение задачи (1.29) в общем виде удается получить только численными методами при рассчете на ЭВМ.

Применимость этих взглядов к лазерному плавлению подтверждается постоянством температуры поверхности металлов в течение некоторого времени при лазерном воздействии с плавно меняющейся плотностью мощности

(рис.1.11).

Удобным параметром для измерений температуры при лазерном воздействии оказывается отражательная способность металлов R . Отражательная способность при увеличении температуры уменьшается, при температуре плавления металла она испытывает резкий скачок, затем продолжает уменьшаться, но уже гораздо медленнее, чем до плавления. Такое поведение отражательной способности позволяет связать ее изменение во время лазерного импульса с изменением температуры.

Типичный вид зависимости отражательной способности металла при лазерном нагревании импульсом длительностью порядка одной микросекунды приведен на рис. 1.11. (В эксперименте использованы отдельные пички лазерного излучения в режиме свободной генерации.)

Область быстрого изменения отражательной способности (левее точки b на рис. 1.11) связывают, естественно, с процессами начального нагревания, а затем плавления поверхностного слоя металла. Постоянство отражательной способности, после того как слой металла, участвующий в поглощении и отражении света, переходит в жидкое состояние (участок bc на рис. 1.11), свидетельствует о постоянстве температуры расплавленного слоя.

В рамках понятий теплопроводности (см. уравнение 1.29) такое поведение температуры на поверхности расплава (участок bc на рис. 1.11) объяснить довольно трудно. Для существования теплового потока к границе фронта плавления необходим градиент температуры в расплаве. При постоянстве температуры поверхности и продвижении границы плавления в глубину градиент температуры должен уменьшаться. Поэтому при достижении на поверхности температуры плавления, даже если весь падающий поток излучения расходуется в

37

этот момент на плавление, по мере продвижения фронта поверхности вглубь, с поверхности должен отводиться все меньший поток, т.е. температура поверхности должна продолжать расти, чтобы фронт плавления продолжал продвигаться вглубь.

Рис. 1.11. Изменение отражательной способности серебра при лазерном воздействии (можно считать, что 1 R A0 aAT ). Пунктиром показана форма импульса. Q = 7.5 кдж/см2. q0max =7 107 вт/см2. q – поглощенный поток лазерного

излучения (q(t) (1 R)qo (t)).

Для оценки времени t2 , в течение которого подводимое к металлу тепло расходуется практически только на фазовый переход, можно использовать предположение о том, что возрастание температуры поверхности не будет происходить до тех пор, пока волна плавления не догонит волну прогрева. Считая,

что средняя скорость первой волны v ~ q(Lm cTm ) 1 , а второй ~ at , можно оценить время t2 следующим образом:

t2 Lm 2cTm , aq

где Lm –- удельная теплота плавления, – плотность, а c – теплоемкость металла и q – средняя плотность потока в течение времени t2 , при q = 1,3•107 Вт/см2 и Lm cTm = 3,4•103 Дж/см3, время t2 ≈ 1,2•10-7 сек, что хорошо согласуется с длительностью участка bc на рис. 1.11.

Для объяснения постоянства температуры поверхности расплава во время плавления при лазерном воздействии можно использовать другой подход.

Увеличение глубины проплавления, как следует из анализа уравнения теплопроводности, снижает подвод теплоты к фронту фазового перехода и уменьшает скорость его перемещения. В свою очередь, это вызывает перегрев поверхностных слоев расплава, что приводит к усилению конвективных пото-

38

ков в расплаве. Интенсивность движения расплава можно оценить по критерию Грасгофа

Gr g 1 Tl0

3

где g – ускорение силы тяжести; 1 – коэффициент объемного расширения;

– кинематическая вязкость, l0 – толщина слоя расплава.

Оценки, выполненные для типичных значений параметров металлов, малых перегревов и сравнительно небольших глубин проплавления ( T <50 К, l0 5·10-4 м), показывают, что Gr 1, т.е. в расплаве происходит его конвективное перемешивание. При этих условиях температура ванны расплава выравнивается, приближаясь к температуре плавления, а перенос теплоты к границе фазового перехода интенсифицируется (a1 ). В результате скорость плавления быстро возрастает, а глубина расплава будет стремиться к предельному для данной плотности потока значению.

Рис. 1.12. Зависимость реальной температуры поверхности Nb при действии прямоугольного импульса Nd-YAG-лазера. Энергия в импульсе 27 Дж. 1 - длительность импульса 3,5 мс, плотность мощности 4,5 105 Вт/см2 и 2 -

длительность импульса 6 мс, плотность мощности 2,5 105 Вт/см2.

Существуют и другие экспериментальные данные о зависимости измеренной температуры от времени при облучении поверхности ниобия (Nb ) излучением Nd-YAG-лазера с различными плотностями мощности, которые приведены на рис. 1.12. Изменение плотности мощности излучения обеспечено изменением длительности прямоугольного импульса при постоянной энергии в импульсе. Характерной особенностью изменения температуры при нагревании является отсутствие горизонтального участка на графике T( t ) при температуре плавления Tп , который обычно связывают с плавлением поверхностного слоя металла. Такой участок существует, но при температуре большей, чем темпера-

39

тура плавления, причем эта температура связана с плотностью мощности лазерного излучения. Между тем при остывании такой горизонтальный участок при Tп существует (см. рис. 1.12).

Таким образом, вопрос о механизме переноса энергии к фронту плавления при постоянной температуре поверхности расплава остается открытым.

Он может быть решен при применении вакансионной модели плавления.

1.2.6.1. Вакансионная модель плавления.

Принимая во внимание отсутствие идеального порядка в кристалле и сохранение некоторой упорядоченности в жидкости, Я.И. Френкель предложил рассматривать процесс перехода кристалла в жидкость как процесс проникновения вакансий в кристалл через его поверхность, при этом вакансии как бы разрыхляют его структуру. Поэтому, в случае простых и, в особенности, одноатомных веществ, процесс аморфизации кристалла можно понимать как процесс образования в кристалле ''вакансионного раствора'', концентрация которого возрастает с ростом температуры. Этот процесс приводит, в конце концов, к плавлению. Исходя из этих представлений об изменении структуры тела при изменении температуры, можно представить себе структуру жидкости как кристалл, деформированный вакансиями.

При больших концентрациях вакансий, когда деформированные области перекрываются, кристаллическая решетка будет деформирована полностью (рис. 1.13 б). В таком, деформированном вакансиями кристалле, атомы, окружающие какой-либо произвольно выбранный атом, располагаются вокруг него преимущественно на тех же расстояниях, что и в кристалле, но с некоторым разбросом - сохраняется ближний порядок. Разброс этот носит случайный характер и быстро возрастает с увеличением расстояния от выбранного атома.

При этом характер кинематики теплового движения у аморфных тел и жидкостей не различается, что и было предсказано Я.И. Френкелем.

Рис. 1.13.. Схема искажения кристаллической решетки вакансиями.

Чтобы понять процесс плавления и получить точное значение температуры перехода, следуя описанной выше модели жидкости, рассмотрим кристалл и жидкость как состояния одной и той же конденсированной фазы, отличающиеся только концентрацией вакансий.

Проанализируем зависимость свободной энергии кристалла F от концентрации вакансий n с учетом их парного взаимодействия. Предположим,